Характеристики урока (занятие)
Уровень образования: основное общее образование
Целевая аудитория: Учащиеся, учителя
Класс: 8 класс
Предмет: Алгебра
Учитель: Двойнова М.В.
Цель: создание условий для передачи опыта по применению деятельностного метода обучения на уроках математики при решении задач с помощью рациональных уравнений.
Задачи:
1. показать способы применения деятельностного метода обучения;
2. отследить эффективность открытого урока через рефлексию участников.
Используемое оборудование: проектор, компьютер, интерактивная доска, учебник «Алгебра» 8 класс «Просвещение 2010» авторы Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, под редакцией С.А.Теляковского.
Урок открытия нового знания. 8 класс, алгебра.
Тема: Решение задач с помощью дробных рациональных уравнений.
Если хотите научиться плавать,
то смело входите в воду, а если
хотите научиться решать задачи,
то решайте их.
Дж. Пойа
Цели урока:
Обучающая:
закрепление понятия дробного рационального уравнения;
составление математической модели задачи, перевод условия задачи с обычного языка на математический;
проверка уровня усвоения темы путем проведения проверочной работы.
Развивающая:
развитие умения правильно оперировать полученными знаниями, логически мыслить;
развитие интеллектуальных умений;
развитие умения принимать решения.
Воспитательная:
воспитание познавательного интереса к предмету;
воспитание самостоятельности при решении учебных задач;
воспитание воли и упорства для достижения конечных результатов.
Задачи: 1) актуализировать знание решения дробных рациональных уравнений, умение решать задачи при помощи рациональных уравнений; добиться усвоения алгоритма решения задач;
2) УУД: — Познавательные: овладение основами логического и алгоритмического мышления;
Регулятивные: развитие умения читать и записывать информацию в виде различных математических моделей, планировать действия в соответствии с поставленной задачей;
Коммуникативные: строить высказывания, аргументировано доказывать свою точку зрения;
Личностные: развитие навыков сотрудничества со сверстниками,
3) — воспитывать чувство товарищества.
Оборудование: презентация, конспект урока, компьютер, проектор, интерактивная доска.
Ход урока:
Организационный момент.
Сегодня у нас необычный урок. У нас присутствуют гости, и на уроке мы немного попутешествуем. Тему нашего урока мы сформулируем вместе, я приготовила вам подсказку в виде ребуса, отгадав его вы сможете, сказать чему будет посвящен наш сегодняшний урок.

Правильно, наш урок посвящен задачам, и не простым, а задачам на составление дробных рациональных уравнений. Сегодня на уроке мы должны составить алгоритм решения дробных рациональных уравнений. Эпиграфом к нашему уроку я выбрала слова Дж. Пойа: «Если хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их». решать задачи мы будем путешествуя по островам с заданиями. Итак, начинаем наше путешествие.
Актуализация знаний.
Первый остров «Теоретик». Ответьте, пожалуйста, на следующие вопросы:
Какие уравнения называются дробными рациональными?
Алгоритм решения дробных рациональных уравнений.
От острова теоретик отправляемся на остров «Практик». Здесь побывал двоечник он выполнил задание, которое предназначалось вам и теперь нам нужно его проверить и исправить ошибки.
При каких значениях переменной выражение имеет смысл:
а) 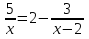 ; б)
; б) 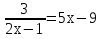 ; в)
; в) 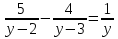 ; г)
; г) 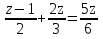 .
.
Остров «Исторический». Историческая справка (сообщение учащихся). Квадратные уравнения в Индии (см. стр. 22 «История математики в школе» Г.И.Глейзер). Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. Индийским математиком и астрономом Ариабхаттой. Другой индийский учёный, Брахмагупта (VIIв.) изложил общее правило решения квадратных уравнений, приведённых к единой канонической форме: ах2 +bх =c, а > 0
В уравнении коэффициенты, кроме а, могут быть и отрицательными.
В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звёзды, так учёный человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи».
Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары:
«Обезьянок резвых стая
Власть поевши, развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась.
А двенадцать по лианам…,
Стали прыгать, повисая…
Сколько ж было обезьянок,
Ты скажи мне, в этой стае?»
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений. Соответствующее задаче уравнение:
 2+12 = х
2+12 = х
Бхаскара решает так:
х2 – 64х = -768
х2 – 64х +322 =-768+322
(х-32)2 =256
х-32 = ±16
х1 =16 х2 =48
Остров «Вспомни». (работа на интерактивной доске)
Необходимо заполнить таблицу, где а, b – коэффициенты квадратного уравнения ax2+bx+c=0 D-его дискриминант, N— число корней уравнения и х1, х2 — корни этого уравнения.
| Уравнение | а | b | c | D | N | х1 | х2 |
| 2х2=0 х2+4х=0 х2-9=0 х2+5=0 5х2+2=0
|
|
|
|
|
|
|
|
Остров «Посчитай-ка».
На этом острове живёт незнайка который не умеет решать задачи. Давай те поможем ему.
Расстояние между городами 40 км. Незнайка ехал на велосипеде и добрался до пункта назначения за  ч, а Знайка поехал на машине и добрался до цветочного города за 20 минут. У кого скорость больше и на сколько?
ч, а Знайка поехал на машине и добрался до цветочного города за 20 минут. У кого скорость больше и на сколько?
40: =40:
=40: =30 км/ч – Незнайка
=30 км/ч – Незнайка
40: =120 км/ч – Знайка
=120 км/ч – Знайка
120 -30=90 км/ч
Ответ: У Знайки, 90 км/ч.
На катере расстояние между двумя пристанями можно проехать за 12 минут со скоростью 50 км/ч. На лодке это же расстояние можно преодолеть за 2 часа. Найдите скорость лодки.
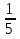 *50=10км – расстояние между пристанями
*50=10км – расстояние между пристанями
10/2=5 км/ч – скорость лодки
Ответ: 5км/ч.
Из двух пунктов реки одновременно навстречу друг другу вышли две моторные лодки. Через 1,2 ч они встретились. Собственная скорости лодок равны 18 км/ч, скорость течения реки равна 2 км/ч. Найти расстояние между пунктами.
1,2*20=24 км – расстояние которая прошла лодка по течению
1,2*16=19,2 км – расстояние которая прошла лодка против течения
24+19.2=43,2 км
Ответ: 43,2 км
Остров «Формул». Для того что бы решать задачи нам необходимо вспомнить формулы. На доске составить формулы для нахождения пути, времени, скорости, скорости при движении по реке по течению, против течения. Пока один человек работает у доски, остальные на местах собирают домино из формул.
3. Объяснение нового материала.
Остров «Новый». На этом острове нам нужно решить задачу. У вас на столах лежит лист с задачей, краткая запись уже частично сделана, вам необходимо решить задачу с помощью уравнения.(Один человек составляет уравнение на интерактивной доске)
Задача 1
Автобус-экспресс отправился от вокзала в аэропорт, находящийся на расстоянии 60км от вокзала. Пассажир, опоздавший на 5 минут на автобус, решил добраться до аэропорта на такси. Скорость такси на 10км/ч больше скорости автобуса. С какой скорость ехал автобус, если он приехал в аэропорт одновременно с такси?
| Скорость, км/ч | Время, ч | Путь, км | |
| Автобус | Х | 60/Х | 60 |
| Такси | Х+10 | 60/(Х+10) | 60 |
Уравнение;
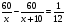 (В тетрадях сделать подробную запись решения.)
(В тетрадях сделать подробную запись решения.)
720(х+10) – 720х= х (х+10)
Ответ; 80км/ч
Вопросы по решению;
Что означает дробь 1/12?
Сравните дроби 60/х и 60/(х+10)
Являются ли корни полученного уравнения решениями задачи?
Физкультминутка.
Первичное закрепление.
Задача №618. Из города в село, находящееся от него на расстоянии 120 км, выехали одновременно два автомобиля. Скорость одного была на 20 км/ч больше скорости другого, и поэтому он пришел к месту назначения на 1 ч раньше. Найдите скорость каждого автомобиля.
| Скорость, км/ч | Время, ч | Путь, км | |
| 1 авто | Х | 120/Х | 120 |
| 2 авто | Х+20 | 120/(Х+20) | 120 |
Решение. Составление математической модели:
х км/ч скорость первого автомобиля;
(х +20) км/ч – скорость второго автомобиля;
 — время первого автомобиля;
— время первого автомобиля;
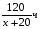 — время второго автомобиля.
— время второго автомобиля.
Согласно условию,
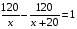 .
.
Работа с составленной моделью.
Решив полученное уравнение, находим  ,
,  . -60 не удовлетворяет условию задачи. 40+20=60 км/ч
. -60 не удовлетворяет условию задачи. 40+20=60 км/ч
Ответ на вопрос задачи.
5. Выполнение контролирующего задания по изученной теме и включение в систему знаний повторение.
Остров «Сам». Самостоятельная работа. Тест.
Работаем хорошо, но чтобы получить полное удовлетворение от своей проделанной работы, надо проверить, как мы научились ее делать. Для этого вам предлагаю решить небольшой тест.
(Ученики работают индивидуально. Выполняют задания, по истечении определенного времени обмениваются работами и проверяют ответы с ключом теста, который находится на экран. Выставляют оценку друг другу в оценочный лист).
| Вариант 2 1. Какие из уравнений являются дробными рациональными? А. 8х + 24 = 3(8 – х2); Б. 2. Даны выражения: 1) А. только 1; Б. только 2; В. 2 и 3; Г. 1, 2 и 3. 3. Уравнение А. 1 и 3; Б. -1, -3 и 11; В. 11; Г. нет решений. 4. Моторная лодка курсирует между двумя пристанями, расстояние между которыми по реке равно 4 км. На путь по течению у нее уходит на 3 мин меньше, чем на путь против течения. Чему равна скорость течения реки, если известно, что скорость лодки в стоячей воде равна 18 км/ч? Пусть х км/ч – скорость течения реки. Какое из уравнений соответствует условию задачи? А. Г. 4(18 + х) – 4(18 – х) = 3. 5. Уравнение А. 1 и 2; Б. 1; В. -2 и 2; Г. 2, -2 и 1.
|
Ключ к тесту:
| 1 | 2 | 3 | 4 | 5 | |
| 1 | Б, В | Б | А | Б | Б |
| 2 | Б, Г | В | В | В | Б |
6.Итог урока
Остров «Копилка». У каждого из вас есть математическая копилка которая находится в голове сегодня вы должны положить в неё алгоритм решения задач с помощью дробных рациональных уравнений. Давайте сформулируем его.
Алгоритм решения задач с помощью дробных рациональных уравнений:
1.Читаем задачу несколько раз;
2. Составляем краткую запись (таблицу);
3. Составляем математическую модель задачи;
4. Работаем с составленной модели;
5. Отвечаем на вопрос задачи (записываем ответ).
Домашнее задание.
Остров «Дом».
Домашнее задание: №619, №620. Придумать условие задачи к уравнению:
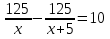 .
.
Рефлексия.
На уроке мы совершили небольшое путешествие по математическим островам и учиться решать задачи с помощью уравнений. Это путешествие подошло к концу. Мне бы хотелось узнать ваше мнение об этом уроке. Выберете мордочку на экране соответствующую вашему мнению об уроке и нарисуйте её на полях в тетрадях.
Из любого путешествия мы привозим подарки, вы очень хорошо работали приготовила для вас сладкие подарки.
