
 Обобщающий урок по теме «Квадратные уравнения»
Обобщающий урок по теме «Квадратные уравнения» Майорова Любовь Александровна учитель математики
Разделы: преподавание математики
Цели урока : Образовательная: закрепление и обобщение знаний учащихся полученные при изучении темы. Выработка умений и навыков по решению квадратных уравнений различного вида разными способами. Выработка умения выбрать нужный рациональный способ решения. Развивающие: развитие логического мышления, памяти, внимания, умений сравнивать и обобщать, умения выступать с самостоятельными суждениями и отстаивать их. Воспитательные: воспитание трудолюбия, взаимопомощи, математической культуры. Умение работать в группах, развивать познавательную активность и логическое мышление учащихся, развитие интереса к предмету. Тип урока: урок обобщения и систематизации. Ход урока I. Организационный момент: сообщение темы и цели урока. На протяжении нескольких уроков мы рассматривали квадратные уравнения и методы их решения. на этом уроке мы повторим и закрепим знания и умения решения квадратных уравнений различными способами. Каждый из вас должен уметь правильно, быстро и рационально решать квадратные уравнения. Эта тема очень важна в курсе математики, она является первой ступенькой в изучении более сложного материала. Вам дан ключ к решению квадратных уравнений, и если вы научились ими пользоваться, вы сможете решать любое квадратное уравнение. А сегодня вы покажите, насколько готовы пользоваться этим ключом.
2.Повторение теоретического материала. Вопросы: 1) Дайте определение квадратного уравнения. 2) Какие квадратные уравнения называются неполными? 3)Сколько видов неполных квадратных уравнений вы знаете? Какие решения они имеют? 4) По какой формуле вычисляется дискриминант полного квадратного уравнения? 5) По какой формуле находят корни квадратного уравнения? 6)Дайте определение приведенного квадратного уравнения. 7) Какие дополнительные формулы вычисления корней квадратного уравнения вы знаете? 8) Как читается теорема Виета? 3.Закрепление изученного материала. У доски работают пятеро учащихся, которые выполняют следующее задание: решить уравнение и все о нем рассказать. 1) х2 +8х=0 2) х2 – 4 = 0 3) 2х2-9х-5=0 4)3х2+6х-9=0 5) х2-5х+6=0 4. Задания для устной работы: А).Задание на определение вида уравнения. Ребята, здесь вы видите уравнения определенные по какому-то признаку. Как вы думаете, какое из уравнений каждой группы лишнее. Ответ: А: 3- лишнее, т.к. это полное квадратное уравнение, а 1;2;3-неполные квадратные уравнения. Б: 2-лишнее, т.к. это уравнение общего вида, а 1;2;3- приведенные квадратные уравнения. 2.На доске написаны 4 пары квадратных уравнений: 70х² — 175х +70 1/14х² — 1/2х + 5/7 = 0 2х² — 5х + 2 = 0 х² — 7х + 10 = 0 0,6х² — 0,8х + 0,2 = 0 -√2х² — √2х + √72 = 0 3х² — 4х + 1 = 0 х² + х – 6 = 0 Учащимся предлагается ответить на следующие вопросы: Какое уравнение из пары вам хотелось бы решить? Можно ли от первого уравнения перейти ко второму? Если да, то как это сделать? Какое из этих уравнений можно решить по теореме Виета? Пока учащиеся у доски готовятся, остальным предлагается задание: закончить предложение так, чтобы оно было верным. Вариант 1.а) Если Д меньше 0, то … б) Если Д равен 0, то … в) Произведение корней приведенного квадратного уравнения равно … Вариант 2. а) Если Д больше 0, то … б) Если второй коэффициент квадратного уравнения – четное число, то … в) Сумма корней приведенного квадратного уравнения равна … Выслушиваются ответы ребят, работавших у доски. 
Б)На доске написаны 4 пары квадратных уравнений:
70х² — 175х +70 = 0 1/14х² — 1/2х + 5/7 = 0
2х² — 5х + 2 = 0 х² — 7х + 10 = 0
0,6х² — 0,8х + 0,2 = 0 -√2х² — √2х + √72 = 0
3х² — 4х + 1 = 0 х² + х – 6 = 0
Учащимся предлагается ответить на следующие вопросы:
Какое уравнение из пары вам хотелось бы решить?
Можно ли от первого уравнения перейти ко второму?
Если да, то как это сделать?
Какое из этих уравнений можно решить по теореме Виета?
В). Не решая уравнения, найдите корни: Г). Какие из уравнений не имеют корней. Д)Не решая уравнение
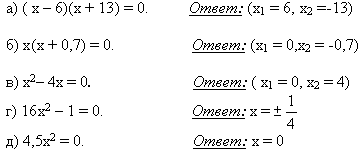
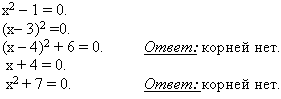
![]() . Найдите:
. Найдите:
-Задание по вариантам (выполняется на отдельных листочках)
Вариант 1. Вариант 2.
1) 2х2-7х=0 1)49=14Х+2Х2 2) -2х2— Х=12 2)Х2-4Х=5
3)Х (Х+3)=0 3)2Х2-8Х=0 4)Х 2=4 4)Х2-9=0
5)5+Х 2=Х 5)Х 2+9Х+14=0
6)5Х2-16Х+3=0 6)3Х2+5Х-2=0
7)2Х-4=0 7)Х-5=0
1.Среди данных уравнений укажите номера тех, которые являются:
а) полными;
б) приведенными;
в) неполными.
2.В уравнении 5) выпишите значения коэффициентов а, в, с.
3)Найдите сумму и произведение корней уравнения 4)Решите уравнение 6.
6.Два ученика решают у доски уравнения:
( х+1)2+(1+х)∙5=14 (х-4)(х+4)=-2х+64
В это время остальные учащиеся участвуют в игре «Расшифруй слово» (Найти корни уравнения и, используя ключ, расшифровать слово)
1) 9х2-1=0
2) х 2+2х=0
3)3х2+5х-2=0
4) (х+1)2-1=0
5) х2-9х+14=0
6) (х+1)2=9
7)2х2-7х+3=0
8) (х+4)2=3х+40
Шифр: А –( 2; 5) О – (0;-2)
Д – (2; 7) Ц – (-4;2)
И – (-2; 8) Ш – (-11;2)
Л – (- 2;1/3) Ы – (1/2;3)
М – (- 1/3;1/3) ! – (-8;3)
ОТВЕТ: должно получиться слово «Молодцы!»
Ученики, работавшие у доски, объясняют свои
решения.
Итоговое тестирование по теме «Решение квадратных уравнений». Тест №1. 1.Какое из уравнений не является квадратным? а). 6х2 + 7х – 6 = 0; б). 2х2 – 7 = 0; в). 10 + 2х 2 = 0; г). 2х3 – 7 = 0. 2.Какое из уравнений является неполным квадратным? а). 3х2 – 8х + 15 = 0; б). 2х2 – 7 = 0; в).5 х2 – 8 х +3 = 0; г). 2х – 5 = 0. 3.Укажите корни неполного квадратного уравнения: х2 – 9 = 0 ). +3 и -3; б). 3 и 6; в). нет корней; г). 0. .4. Выберите неполное квадратное уравнение, не имеющее корней: а). 2х2 + 8 = 0; б). х2 – 3х = 0; в). х2 = 16; г). х2 – 2х = 0. 5. Укажите дискриминант данного квадратного уравнения: 6х2 + 3х – 1 = 0: а). 44; б). 33; в). 0; г). -15. 6.Укажите число корней квадратного уравнения: х2 – 3х + 3 = 0: а). Два различных корня; б). Два совпадающих корня; в). Нет корней; г). Четыре корня. 7. Укажите, не решая, сумму и произведение корней приведенного квадратного уравнения: у2 + 8у +15 = 0:а). х1 + х2 = 8; х1х2 = 15; б). х1 + х2 = 8; х1х2= — 15; в). х1 + х2 = — 8; х1х2 = 15; г). х1 + х2 = -8; х1х2= -15. 8. Один из корней квадратного уравнения равен 3. Найдите второй корень уравнения х2 – 5х + 6 = 0: а). 2; б). 3; в). 6; г). 1. .
Какое уравнение называется квадратным?
Как можно решить полное квадратное уравнение? Неполное?
Сколько корней может иметь квадратное уравнение?
Д/з: №671(а,б) №666
