Федеральное государственное казенное
общеобразовательное учреждение
«Средняя общеобразовательная школа №151»
ПРИЕМЫ
УСТНОГО РЕШЕНИЯ
КВАДРАТНЫХ УРАВНЕНИЙ
Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, иррациональных уравнений и неравенств.
Одна из основных целей изучения школьного курса математики заключается в овладении способами решения алгебраических уравнений второй степени и приводимых к ним уравнений. В школьном курсе изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения. Желательно научить ребят решать квадратные уравнения несколькими способами. Впоследствии при решении других видов уравнений, сводящихся к квадратным, рационально использовать те способы, которые позволяют находить корни квадратных уравнений устно: свойства коэффициентов и способ «переброски» старшего коэффициента.
Данные приемы устного решения квадратных уравнений заслуживают внимания, поскольку не отражены в школьном учебнике математики. Овладение приемами поможет обучающимся экономить время, эффективно решать уравнения, развить математические, интеллектуальные способности, навыки исследовательской работы.
Рассмотрим некоторые приемы устного решения квадратных уравнений.
Приведенные квадратные уравнения.
Наиболее распространенное устное решение приведенных квадратных уравнений, но и оно у многих учеников вызывает затруднение, особенно в случаях, когда корни имеют разные знаки.
Напомним, что приведенное квадратное уравнение это уравнение вида
х2 + рх + q = 0
Корни х1 и х2 удовлетворяют теореме Виета
х1 х2 = q х1 + х2 = — р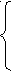
Определить знаки корней без решения уравнения (при условии, D0)
можно по следующим правилам:
| р 0 | р 0 | |
| q | оба корня отрицательны | оба корня положительны |
| q | корни имеют противоположные знаки | |
Рассмотрим случаи.
q 0
Если в уравнении х2 + рх + q = 0 q 0 ( или последним знаком является знак «минус»), то корни имеют разные знаки, причем знак меньшего корня совпадает со знаком второго коэффициента в уравнении ( будем называть его в дальнейшем вторым знаком уравнения, а числа р и q будем называть модули коэффициентов).
Зная, что при сложении чисел с разными знаками их модули вычитаются, сформулируем правило нахождения корней уравнения.
найти такие множители числа q, чтобы их разность была равна числу р;
поставить перед меньшим из найденных чисел второй знак уравнения, другой корень будет иметь противоположный знак.
Пример 1.Решить уравнение х2 – 2х – 15 = 0
Решение.
1) Найдем множители числа 15: 1 и 15, 3 и 5. Выберем те, разность которых равна 2. Это числа 3 и 5.
2)Перед меньшим числом ставим второй знак уравнения, т.е. «минус».
Таким образом, корни уравнения: х1 = — 3, х2 = 5.
Ответ: -3 и 5.
Пример 2. Решить уравнение х2 + 10х – 24 = 0
Решение.
Множители числа 24: 1 и 24; 2 и 12; 3 и 8; 4 и 6 .
10 = 12 — 2 и второй знак уравнения «+» , то х1= 2, х2 = — 12
Ответ: — 12; 2.
Пример 3. Решить уравнение х2 – 5х – 14 = 0.
Решение.
14 = 2 7 и 5 = 7 – 2, то х1 = — 2, х2 = 7.
Ответ: — 2; 7.
Такой алгоритм помогает быстро решать уравнения тем обучающимся, у которых имеются трудности с подбором знаков в теореме Виета.
Задания для самостоятельного решения.
Решите уравнения:
х2 – 4х – 77 = 0 3) х2 + х – 56 = 0
х2 + 8х – 20 = 0 4) х2 – 7х – 8 = 0
Составьте уравнение, корнями которого являются числа:
6 и — 7 3) — 1 и 24
13 и – 9 4) — 5 и 4
Составьте четыре произвольных уравнения с целыми корнями, имеющими разные знаки.
q
Если в уравнении х2 + рх + q = 0 q 0 (или последним знаком является знак «плюс») то уравнение имеет два корня и оба корня имеют одинаковые знаки, противоположные второму знаку уравнения.
Сформулируем правило нахождения корней.
если в уравнении два знака «плюс», то оба корня имеют знак «минус»;
чтобы найти корни, нужно найти такие множители свободного члена q, чтобы их сумма была равна числу р.
Пример 1. Решить уравнение х2 + 7х + 12 = 0.
Решение.
12 = 1 12 = 2 6 = 3 4 и 3 + 4 = 7, а в уравнении два «плюса»,
то корни уравнения х1 = -3, х2 = -4.
Ответ: х1 = -3, х2 = -4.
Пример 2. Решить уравнение х2 – 9х + 14 = 0.
Решение.
14 = 2 7 и 2 + 7 = 9, второй знак «минус», последний знак «плюс»,
значит, корни уравнения х1 = 2, х2 = 7.
Ответ: х1 = 2, х2 = 7.
Задания для самостоятельного решения.
Решите уравнения:
х2 –11х + 24 = 0 3) х2 – 17х + 30 = 0
х2 + 4х + 3 = 0 4) х2 + 9х + 14 = 0
Составьте уравнение, корнями которого являются числа:
5 и 7 3) 11 и 8
— 1 и – 6 4) — 4 и — 20
Таким образом, для нахождения корней приведенного квадратного уравнения
х2 + рх + q = 0 можно применить следующий алгоритм.
Найти множители свободного члена, для которых действие, указанное последним знаком уравнения, дает второй коэффициент;
2. расставить знаки у найденных множителей по следующему правилу:
если в уравнении два «плюса», то в ответе два «минуса»,
если последний знак уравнения «минус», то меньшему корню присваивается второй знак уравнения, больший корень имеет противоположный знак.
Пример 1. Решить уравнение х2 – 7х – 30 = 0.
Решение.
Множители числа 30: 1 и 30; 2 и 15; 3 и 10; 5 и 6.
Последний знак « — », подбираем те, разность которых равна 7. Это 3 и 10. Меньшему числу присваиваем знак « — ».
Таким образом, корни уравнения: х1 = -3 , х2 = 10.
Ответ: х1 = -3 , х2 = 10.
Пример 2. Решить уравнение х2 – 7х + 6 = 0.
Решение.
Среди множителей числа 6 ищем такие, сумма которых равна 7
(последний знак уравнения « + »). Это числа 1 и 6., таким образом, х1 = 1, х2 = 6.
Ответ: х1 = 1, х2 = 6.
Квадратные уравнения вида ax2 + bx + c = 0, a 0.
Свойства коэффициентов квадратного уравнения.
Пусть дано квадратное уравнение ax2 + bx + c = 0, a 0.
Если а + b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1, ![]() — корни этого уравнения.
— корни этого уравнения.
Доказательство:
Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение ![]()
Согласно теореме Виета 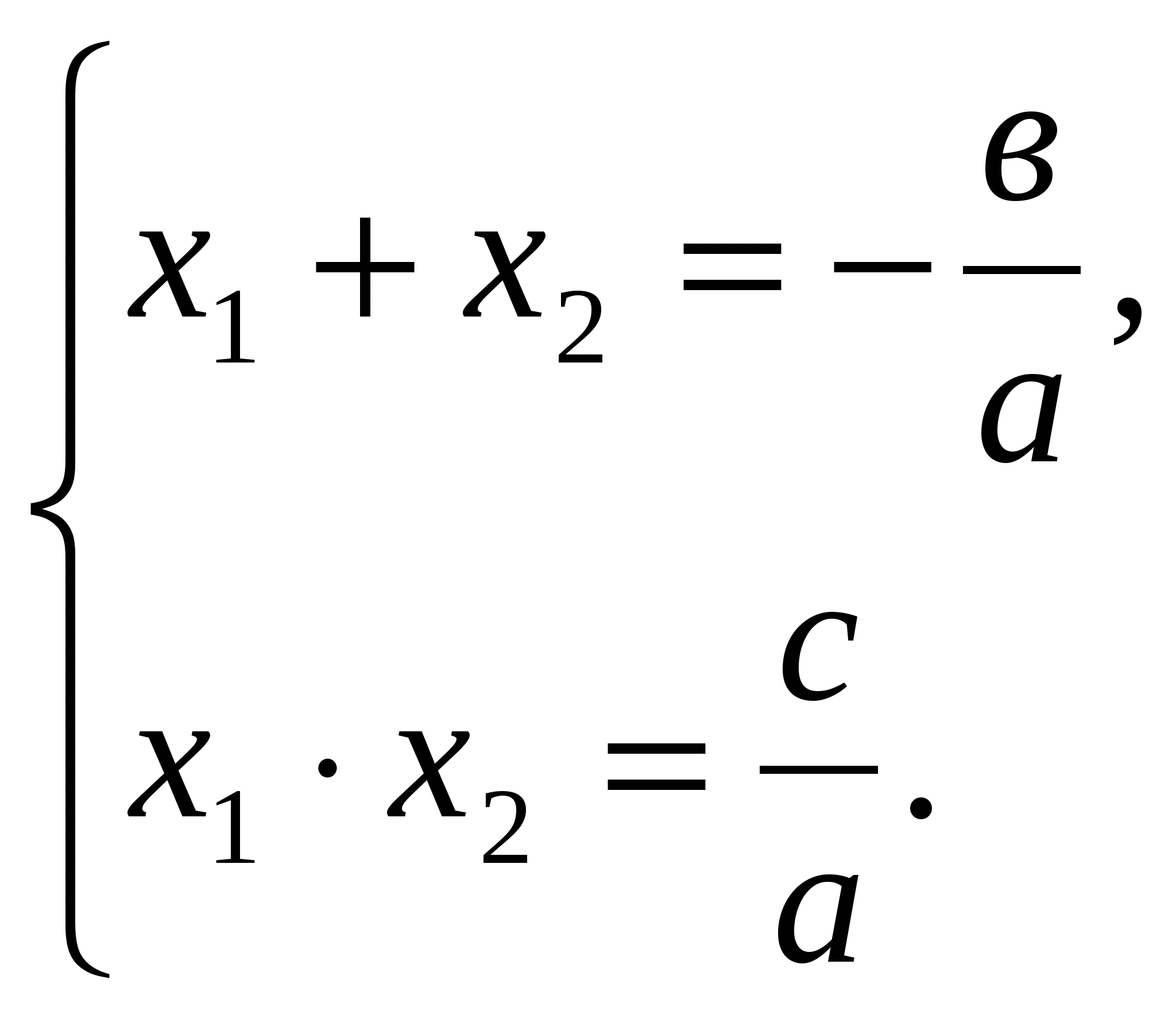
По условию а + в + с = 0, откуда в = — а – с. Значит, 
Получаем: ![]() что и требовалось доказать.
что и требовалось доказать.
2. Если а – в + с = 0, или в = а + с, то ![]()
Доказательство:
По теореме Виета 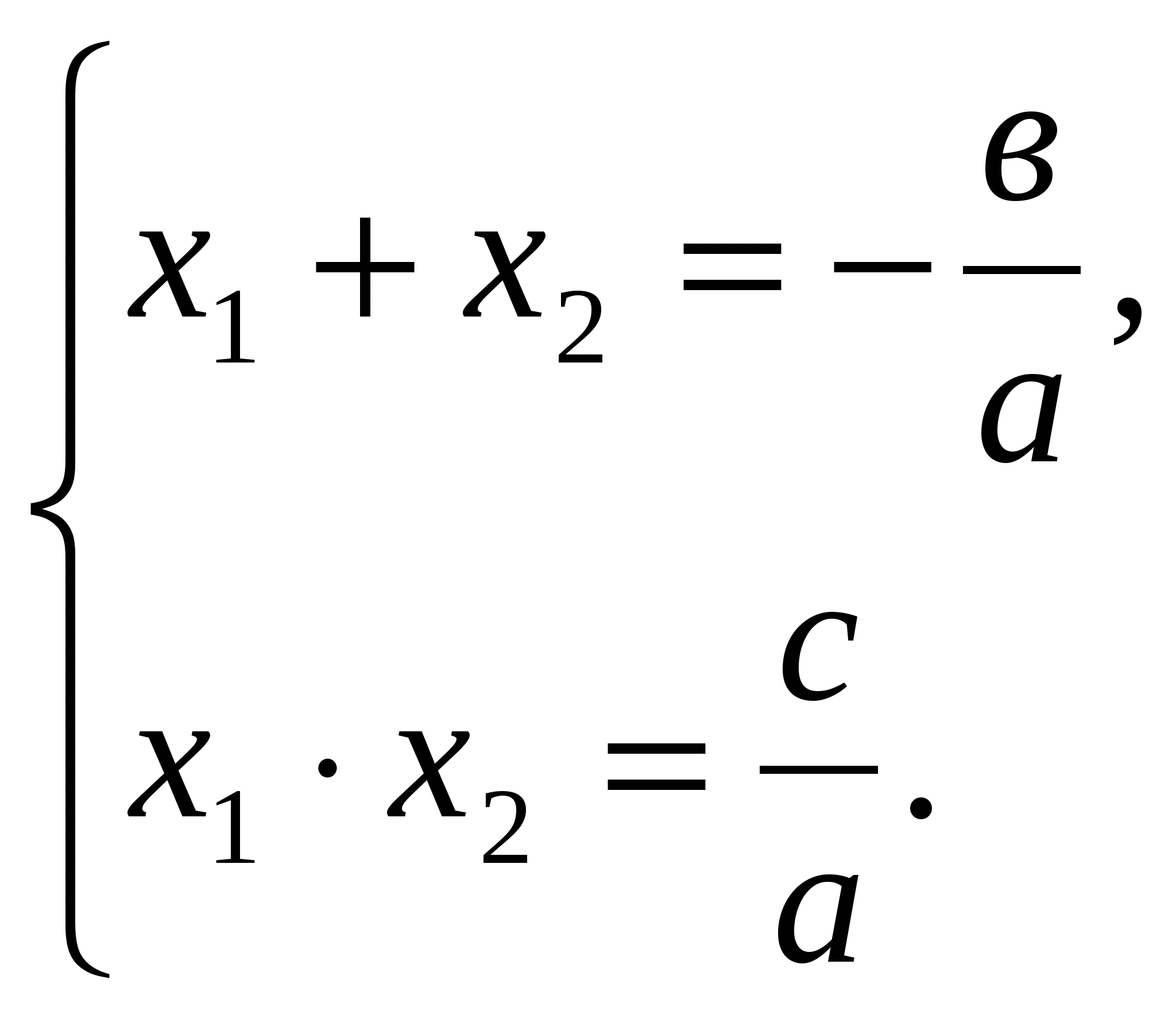
По условию а – в + с = 0, откуда в = а + с. Таким образом, 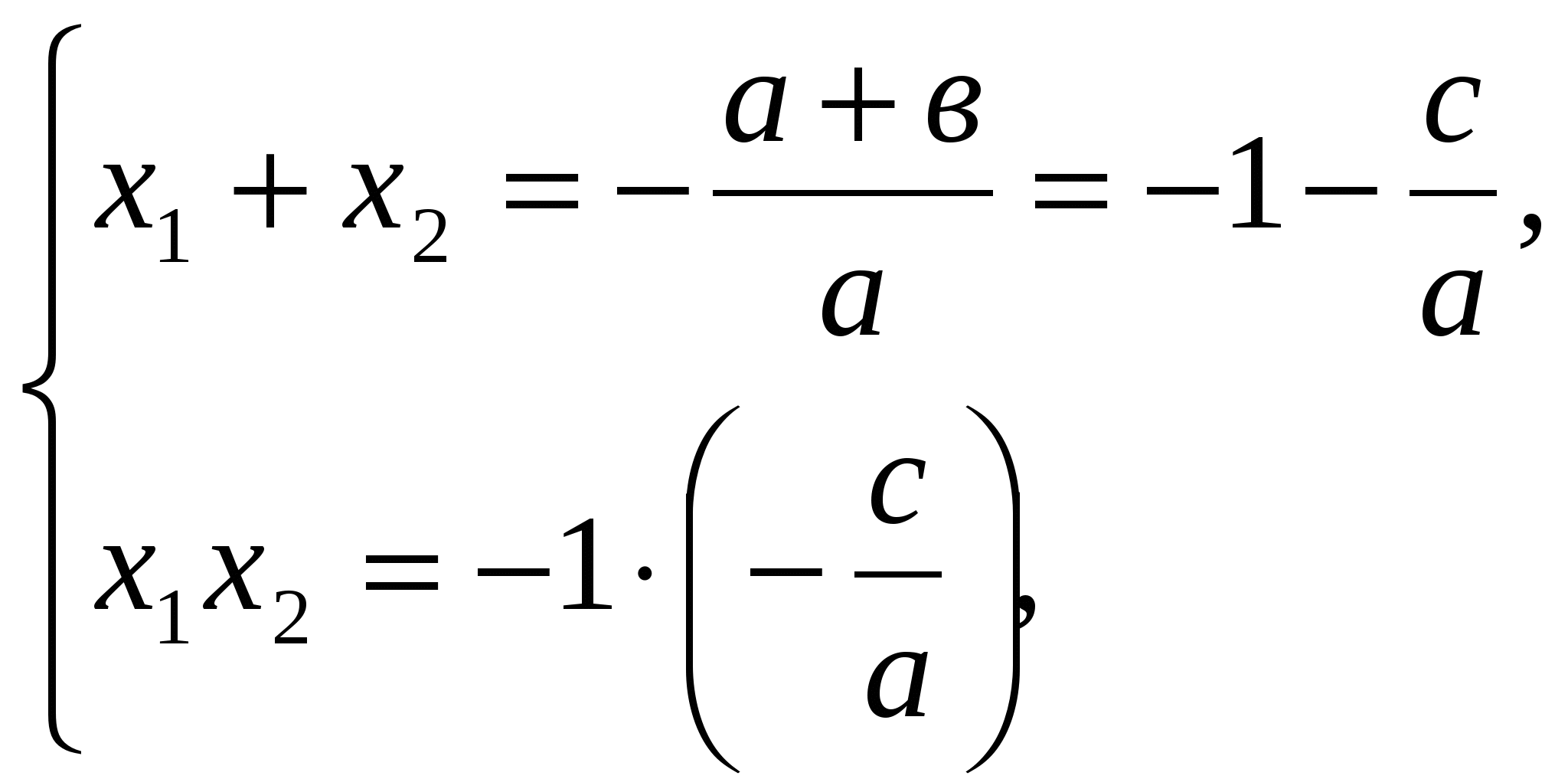
т.е. ![]() что и требовалось доказать.
что и требовалось доказать.
Из свойства коэффициентов следуют приемы устного решения квадратного уравнения – приемы «коэффициентов».
Прием 1. Если а + b + с = 0, то ![]()
Пример 1. Решить уравнение 4х2 – 13х + 9 = 0.
Решение.
Сумма коэффициентов 4 – 13 + 9 = 0, значит, ![]() — корни уравнения. Ответ:
— корни уравнения. Ответ: ![]() .
.
Пример 2. Решить уравнение ![]() = 0.
= 0.
Решение.
Сумма коэффициентов 839 – 448 – 391 = 0 , значит, ![]()
Прием 2. Если b = а + с, то ![]()
Пример 1. Решить уравнение ![]()
Решение.
7 = 2 + 5, значит, ![]() — корни уравнения
— корни уравнения
Ответ: ![]()
Пример 2. Решить уравнение 5х2 + 3х -2 = 0
Решение.
3 = 5 + (-2), значит,![]() .
.
Ответ: ![]()
Решение уравнений способом «переброски».
Если а ± b + с 0, используем метод «переброски коэффициента».
Решим уравнение ![]() Умножим обе части уравнения на a, получим
Умножим обе части уравнения на a, получим ![]() Пусть
Пусть ![]() , откуда
, откуда ![]()
Тогда приходим к уравнению, равносильному данному ![]() Его корни у1 и у2 .
Его корни у1 и у2 .
Окончательно ![]() .
.
При этом способе коэффициент a умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Пример 1.Решить уравнение 3х2 + 2х – 1 = 0
Решение.
3х2 + 2х – 1 = 0, | 3
9х2 + 6х – 3 = 0
(3х )2 + 2 (3х) – 3 = 0
Пусть 3х = у, тогда получим уравнение: у2 + 2у – 3 = 0. Сумма коэффициентов равна нулю: 1 + 2 + 3 = 0, значит, у1 = 1, у2= -3/ 1 = -3.
Вернемся к подстановке: 1) 3х = 1, х = 1/ 3.
2) 3х = — 3, х = — 1.
Ответ: х1 = — 1, х2 = 1/3.
Р ешение может быть таким:
ешение может быть таким:
П ример 2. Решить уравнение 2х2 – 11х + 5 = 0
ример 2. Решить уравнение 2х2 – 11х + 5 = 0
Решение.
«Перебросив» коэффициент, получим приведенное квадратное уравнение
х2 — 11 х + 10 = 0, корни которого 1 и 10. Делим каждое число на 2, получаем корни данного уравнения: х1 = 0,5, х2 = 5.

Пример 3. Решить уравнение 6х2 – 7х – 3 = 0.
Решение.
«Перебросив» коэффициент, получим приведенное квадратное уравнение
х2 – 7х – 18 = 0, корни которого 9 и – 2.
Делим на ![]() ,
, ![]() — корни данного уравнения
— корни данного уравнения
 Ответ:
Ответ: ![]() .
.
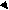
Пример 4. Решить уравнение ![]()
Решение:
Используя метод «переброски», получим уравнение
![]()
По теореме Виета 
Ответ: ![]()
Задания для самостоятельного решения.
Решить уравнения:
5х2 — 7х +2 =0 1) 5х2 — 7х -12 =0
11х2 +25х — 36=0 2) 11х2 +25х +14=0
345х2 -137х -208=0 3) 3х2 +5х +2=0
3х2 +5х — 8=0 4) 5х2 + 4х — 1=0
5х2 + 4х — 9=0 5) х2 + 4х +3=0
2х2 -9х +9=0
10х2 -11х + 3=0
3х2 +11х +6=0
6х2 +5х — 6=0
3х2 +1х — 4=0
Литература.
Мордкович А. Г.. Алгебра 8 кл. Учебник для общеобразовательных учреждений.// М. Мнемозина.- 2012 г.
Плужников И. Г. « 10 способов решения квадратных уравнений» //Математика в школе.-2000.- № 40.
Михайлова Ж. Н. Алгоритмы – ключ к решению задач по алгебре. Ч 1.// М. Просвещение.-2008г.
