Урок 81. 6 Решение квадратных неравенств методом интервалов.
учитель математики СШ №19, г. Актобе Испимбетова А.Т.
Цель урока: Проверить умение решать квадратные и дробно-рациональные неравенства методом интервалов.
Образовательные: а). Обобщение и систематизация знаний учащихся по теме «Неравенства».
б). Закрепление навыков решения заданий по теме решение неравенств методом интервала.
Развивающие:
а). Формирование и развитие умения мыслить и анализировать.
б). Развитие памяти.
Воспитывающие:
а). Воспитание умения работать самостоятельно.
б). Воспитание умения выдерживать регламент времени, отведенного на решение каждого задания.
в). Привитие интереса к предмету.
1. Организационный момент и приветствие.
2. Повторение: устный опрос и устный счет.
3. Закрепление. Решение квадратных и дробно-рациональных неравенств методом интервалов.
4. Физминутка.
5. Самостоятельная работа.
6. Домашнее задание .
7. Рефлексия.
1. Организационный момент и приветствие.
Приветствуют гостей, друг друга . Показывают свой смайлик с настроением.
Выбирают карточки и делятся на группы.
Прозвенел звонок для нас!
Встали все у парт красиво;
Поздоровались учтиво,
Тихо сели, спинку прямо.
Все легонечко вздохнем,
Урок алгебры начнем.
2. Повторение:
1. Что называем линейным неравенством?
2. Какое выражение называется квадратным неравенством?
3. Какие способы решение квадратных неравенств, знаете?
4. Алгоритм решение квадратных неравенств?
5. Алгоритм решение квадратных неравенств методом интервалов?
6. Устный счет. Вспомним как решать.
№1. Известно, что 0<a<b. Какое из следующих чисел положительно?
2а — 2в; 2) (а+3)·(-в); 3) (а-в)/10; 4) (а-5в)·а
№2. На координатной прямой отмечены числа а, в и с. Какое из приведенных утверждений об этих числах неверно?
b – c > 0; 2) a + b < 0; 3) ba > 0; 4) abc < 0.
№3. Решите линейное неравенство: 3х – 5 ≥ 7х – 15.
№4. Решите неравенство методом интервалов:
а) х2>16 б) х2+5>0 в) х2+ 5<0
№5. Решите квадратное неравенство: х2+7х-8<0
3.Закрепление.
Решение квадратных и дробно-рациональных неравенств методом интервалов.
Письменно решаем № 302, № 303,№ 304, №305 (нечетные)
№302 1) -2х2-5х+3≤0; 2) 5х2-2х-3≤0.
№303 1) 2х2-3х+1> 0; 2) -35х2-12х-1<
4. Физминутка.
Потрудились- отдохнем.
Встанем- глубоко вздохнем.
Руки в стороны, вперед, влево, вправо, поворот.
Три наклона, прямо встань.
Руки вниз, затем поднять
Руки плавно опустили, всем улыбку подарили.
5. Самостоятельная работа.
« Незнающие пусть научатся, знающие- вспомнят ещё раз»
1) На координатной прямой отложено число а :
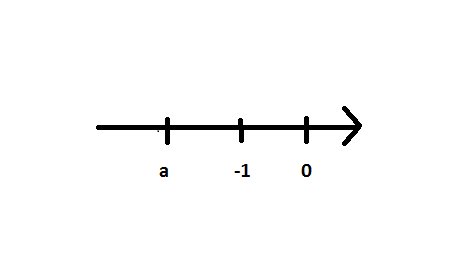
Расположите в порядке убывания числа а, 1/а, а2
1) а, 1/а, а2 ; 2) 1/а, а, а2 ; 3) а2, 1/а, а ; 4) а2, а, 1/а .
2) Из указанных неравенств выберите верное:
1) 0,6
3) 3/8<0,6<4/3 ; 4) 4/3<0,6<3/8
3) Решите неравенство:
3х+5 < х-7
1) (-∞; 6) ; 2) (6; + ∞) ; 3) (- ∞; -6) ; 4) (-6; + ∞).
4) Решите неравенство:
Х2 ≥ 9
1) (-∞; -3] ; 2) [-3; 3] ; 3)[3; +∞) ; 4)(-∞;-3]U[3;+∞)
5) Решите неравенство:
х2+4х-5 ≤ 0
1) (-∞;-5)U(1;+∞) ; 2) [-5; 1]; 3) (-∞;-5]U[1;+∞); 4) (-5; 1).
1) О числах а, в и с известно, что с>b>a.
Какое из следующих чисел отрицательно?
1) с – в ; 2) в – а ; 3) а – с; 4) с — а
2) Из указанных неравенств выберите верное:
1) 0,5
3) 0,5
3) Решите неравенство:
Х+7 > 6-3х
1) (-1/4; + ∞); 2) (1/4; + ∞); 3) (- ∞; -1/4); 4) (- ∞; 1/4)
4) Какое из указанных неравенств верно при любом значении Х?
1) х2-2>0 ; 2) х2+2≥0; 3) х2-2≤0; 4) х2+2<0.
5) Решите неравенство:
х2-5х+4 < 0
1) (-∞;1)U(4;+∞) ; 2) [4;5]; 3) (-∞; 1); 4) (1;4).
1) Известно, что a<b. Какое из следующих неравенств неверно?
1) в+4 > а+4 ; 2) 2в+1<2(1/2+а); 3) а – в а-2
2) Из указанных неравенств выберите верное:
1) 0,6
3) 5/6<0,6<3/7; 4) 3/7
3) Решите неравенство:
1-3х ≤ 2х-9
1) х ≥ 2 ; 2) х ≥ -2; 3) х ≤ -2; 4) х ≤ 2
4) Решите неравенство:
Х2 < 4
1) (-∞;-2)U(2;+∞) ; 2) (-2; 2); 3) (-∞;-2]U[2;+∞) ; 4) [-2; 2].
5) Решите неравенство:
(х-2)(х+3) ≥0
1) [-3;+∞); 2) [2;+∞); 3) [-3; 2]; 4)(-∞;-3]U[2;+∞).
1) О числах а, с, х и у известно, что х > у, с = х, а > с.
Сравните числа у и а.
1) у > а ; 2) у = а
3) у < а 4) сравнить нельзя
2) Из указанных неравенств выберите верное:
1) 4/5<0,7<1/2; 2) 1/2<0,7<4/5
3) 1/2
3) Решите неравенство:
Х-4 ≥ 5х+8
1) [-3; + ∞); 2) [3; + ∞); 3) (- ∞; -3]; 4) (- ∞; -2].
4) Какое из указанных неравенств не выполняется ни при каком значении Х?
1) х2+1≤0 ; 2) х2+1>0; 3) х2 ≥ 1; 4) х2 ≤ 1.
5) Решите неравенство: х2 + х-2≤ 0.
1) [-1;2]; 2) (-∞;1)U(2;+∞); 3) [0; 2]; 4) [-2; 1]
6. Домашнее задание .
№ 302, № 303,№ 304, №305 (четные)
7. Рефлексия. 1. Чему научились на уроке?
2. Что показалось легким?
3. В чем испытывали затруднение?
4. Над чем ещё нужно поработать?
5. Как оцениваете свою работу?
«Человек подобен дроби: в знаменателе-то, что он о себе думает, в числителе-то, что есть на самом деле. Чем больше знаменатель, тем меньше дробь» (Лев Толстой)
