Конспект урока по Алгебре «Графический способ решения система уравнений с двумя переменными» 10 класс

Урок алгебры в10 классе по теме: «Графический способ решения система уравнений с двумя переменными».

Цель урока: добиться усвоения учащимися смысла понятий: что значить решить систему уравнений с двумя переменными, алгоритма решения системы уравнений с двумя переменными графическим способом. Уметь решать и оформлять задание на соответствие между объектами.

Тип урока: усвоение знаний, формирование умений.

Оборудование: опорный конспект

План изучение нового материала

1. Понятие системы уравнений с двумя переменными и ее решение.

2. Алгоритм решения системы уравнений с двумя переменными графическим способом.

Ход урока

I Организационный этап

1. Учитель проверяет готовность к уроку, настраивает их на работу.

2. Проверка домашнего задания № 412 (б, д), № 404

Решить неравенство:

б) ; д)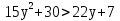

№ 404

Запишите уравнение окружности с центром в начале координат, зная, что она проходит через точку.

А (-2; ), В (3; 4); С (8; 0)

II Актуализация опорных знаний и умений учащихся

Устные упражнения:

1) Является ли пара чисел (2;0) решением уравнения:

а) 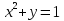б) ху+3 = 0 в) у (х+2) =0

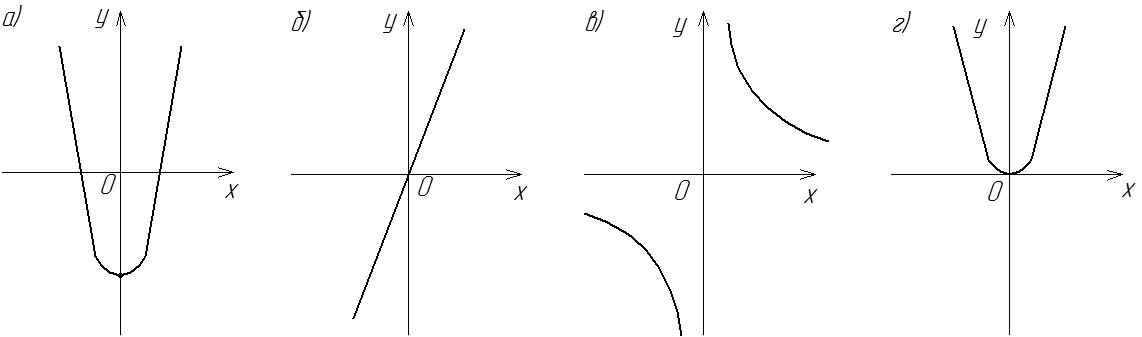
2) Выберите схематичный график функции:

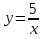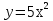1) у=5х 2) 3) 4)

III Усвоение знаний

Опорный конспект

Если ставится задача найти все общие решения двух (и более) уравнений с двумя переменными, то говорят, что нужно решить систему уравнений с двумя переменными.

Решением системы уравнений с двумя переменными х и у называется такая пара значений переменных (х; у), которая является решением каждого из уравнений системы.

Например: пара (2; 3) является решением системы уравнений 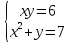; так как х=2 и у=3 является решением каждого из уравнений системы.

Решить систему уравнений с двумя переменными значит найти все ее решения или доказать, что их нет.

Если система не имеет решений, ее называют несовместимой.

Алгоритм решения системы уравнений с двумя переменными х и у графическим способом

1. Строим графики каждого из уравнений системы в одной прямоугольной системе координат.

2. Находим все точки пересечения построенных графиков и определяем их координаты. Эти координаты и являются решениями данной системы уравнений.

Объяснение учителя:

Пусть требуется решить систему уравнений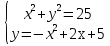

Построим в одной системе координат графики уравнений и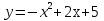

Координаты любой точки окружности являются решением уравнения , а координаты любой точки параболы – решением уравнения 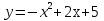. Значит, координаты любой точки пересечения окружности и параболы удовлетворяют как первому уравнению системы, так и второму. Используя рисунок, находим приближение значения координат точек пересечения графиков:

А (-2,2; 4,5), В (0; 5), С (2,2; 4,5), Д (4; -3).

Следовательно, система имеет четыре решения. Подставив найденные значения в уравнения системы, можно убедится, что В (0; 5), Д (4; -3) являются точками, а А (-2,2; 4,5) и С (2,2; 4,5) – приближенными.

IV Физкультминутка

V Решение тренировочных упражнений: № 415

Является ли решением системы уравнений: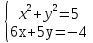

пара чисел: а) (-2; 1), (1; -2) ?

№ 416

Решите графически систему уравнений:

Работа в парах: № 419

С помощью графиков решите систему уравнений:

VI Подведение итогов

1. Известно, что система уравнений

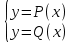имеет три решения.

Сколько точек пересечения имеют графики этих уравнений.

2. Используя график на рисунке (на доске) найдите решения системы уравнений.

Домашнее задание: П. 18, решать № 417, №376.