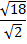
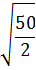
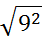
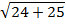
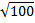
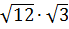
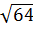
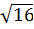
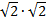
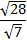
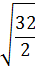

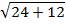
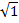
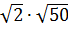
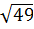
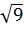
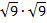
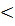 Урок алгебры в 8 классе
Урок алгебры в 8 классе
Тема «Преобразование выражений содержащих квадратные корни»
| ФИО (полностью) | Козлова Лидия Николаевна | |
|
| Место работы | Тенистовская общеобразовательная школа I—IIIступеней Бахчисарайского районного совета РК |
|
| Должность | учитель математики |
|
| Предмет | алгебра |
|
| Класс | 8 |
|
| Базовый учебник Алгебра 8. / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Пешков, С.В. Суворова. Под редакцией С.А. Теляковского. / М.: Просвещение, 2009.
| |
Цели урока:
Формирование у учащихся знаний о разложении выражений, содержащих квадратные корни на множители с использованием формул сокращенного умножения.
Развитие умений использовать ранее полученные знания при разложении на множители выражений содержащих корни.
Воспитывать собранность, умение самостоятельно действовать, интерес к предмету.
План урока.
Организационный момент.
Сообщение темы урока .
Ребята каждый из вас сегодня получил «фигуренка» в течение урока на каждом этапе вы будете закрашивать какую – то его часть цветами светофора: зеленый- все понятно, желтый – есть вопросы, красный – сложно, нужно разобрать еще раз .
Историческая справка
Арифметический корень произошел от латинского слова radix – корень, radicalis – коренной
Начиная с 13 века итальянские и другие европейские математики обозначали корень латинским словом radix ( сокращенно r). В 1525 г. в книге Х.Рудольфа “Быстрый и красивый счет при помощи искусных правил алгебры, обычно называемых Косс” появилось обозначение V для квадратного корня,VVV-для кубического. В 1626 г. голландский математик А. Жирар ввел обозначения V, V и т. д., которые вскоре вытеснили знак r, при этом над подкоренным выражением ставилась горизонтальная черта. Современное обозначение корня впервые появилось в книге Рене Декарта “Геометрия”, изданной в 1637 году
Актуализация опорных знаний
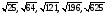 Устная работа
Устная работа
Вычислить:
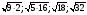 Вынести множитель из-под знака корня:
Вынести множитель из-под знака корня:
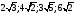 Внести множитель под знак корня:
Внести множитель под знак корня:
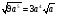 Найти ошибку
Найти ошибку
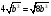
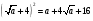
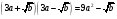
Работа в группах. «Проверка умения работать со словарем правовой терминологии»
Самостоятельная работа
На столе у каждого учащегося лежит лист с текстом самостоятельной работы. Выполняя самостоятельную работу обучающиеся расшифровывают слово. Получив ответ в задании №1, вы ищите такой же в 1-ой строке таблицы, и букву, соответствующую этому ответу выписываете. Таким образом, поступаете до конца самостоятельной работы. Решив все задания, вы получаете слово. Если вам не удалось его получить, значит, вы не достаточно усвоили решение предложенных типов заданий, и вам нужно продолжить работу по их изучению.
После того, как время самостоятельной работы закончилось, учитель подводит итоги работы по вариантам. На экран с помощью проектора выводятся слово, которые учащиеся должны расшифровать, решая задания. Если ученики не до конца справились с самостоятельной работой или сделали ошибки, то дома нужно будет выполнить анализ ошибок, а так же придумать и решить задания подобные нерешенным.
Упростите выражение
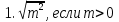 ,
,
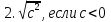 ,
,
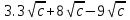 .
.
Что больше – А или В, если
А = 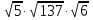
В = 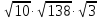
Выполните действия
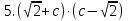
Сколько множителей должно быть в знаменателе дроби, чтобы равенство было верным? 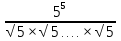 = 1.
= 1.
Решение:
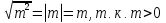 ,
,
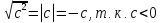 ,
,
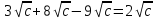 ,
,
АВ, т.к. А = 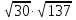 ; В =
; В = 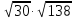
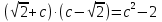 ,
,
10 множителей.
| А | Р | М | О | Л | Ь | |
| | —m | -2m | m |
| m2 | —m2 |
| | c |
| 2c | —c | —c2 | — |
| | 3 | 2 | -2 | 2c | 20c | -2c |
| | А<В | А=В | А>В | А≤В | А≥В | А≠В |
| | c2+2 | c-2 |
|
|
c2-2 |
|
| | 9 | 5 | 8 | 6 | 2 | 10 |
Тот, кто, верно решил самостоятельную работу, получил слово МОРАЛЬ.
Мораль – это совокупность особых, духовных правил, регулирующих поведение человека, его отношение к другим людям, к самому себе, а также к окружающей среде. Смысл морали воплощен в «золотом правиле»: поступай по отношению к другому так, как ты хотел бы, чтобы он поступал по отношению к тебе.
III. Работа по формированию навыков работы с дробями
1. Разложите на множители.
|
|
|
| ( | |
| б) 16 – в , в≥0 |
|
|
| (4 — |
| в) 13 + 3 |
|
|
|
|
| г) 7 — 2 |
|
|
|
|
Ученики решают в тетрадях по вариантам, 2 человека (по одному от каждого варианта) решают у доски.
2. Сократите дробь.
|
|
|
| а — | |
| б) |
|
|
|
|
| в) |
|
|
|
|
| г) |
|
|
|
|
| д) |
|
|
|
|
| е) |
|
|
|
|
Ученики решают в тетрадях по вариантам, 4 человека решают у доски. Примеры д и е решают дополнительно, кто успеет.
3. Освободитесь от иррациональности в знаменателе дроби.
|
|
|
|
| |
| б) |
|
|
|
|
| в) |
|
|
|
|
| г) |
|
|
| 2( |
Ученики решают по вариантам, 2 человека решают по 2 примера у доски.
Физкультминутка
Какой ряд быстрее посчитает до 10. (На доске вывешены две таблицы.
Выходят по очереди и указывают где зашифровано число, которое ему надо назвать)
«Умение проводить экспертизу».
IV. Учимся быть экспертами. Работа в группах.
1 группа:
Проверить, является ли число (4 + 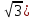 корнем уравнения х2 – 8х + 13 = 0.
корнем уравнения х2 – 8х + 13 = 0.
Решение:
( 4 + 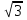 )2 —
)2 — 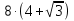 + 13 =0;
+ 13 =0;
16 + 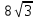 + 3 – 8
+ 3 – 8 4 — 8
4 — 8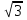 + 13 = 0
+ 13 = 0
0=0.
Ответ: число 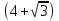 является корнем уравнения.
является корнем уравнения.
2 группа:
Проверить, является ли число ( 4 — 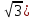 корнем уравнения х2 – 8х + 13 = 0
корнем уравнения х2 – 8х + 13 = 0
Решение:
(4- 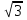 )2 —
)2 — 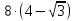 + 13 =0;
+ 13 =0;
16 — 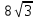 + 3 – 32 + 8
+ 3 – 32 + 8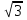 + 13 = 0.
+ 13 = 0.
0=0.
Ответ: число (4 — 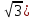 является корнем уравнения.
является корнем уравнения.
Представители групп защищают свою работу.
Дополнительные задания.
Сократите дроби и сравните их значения:
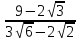 и
и 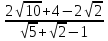 .
.
Решение.
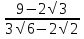 =
= 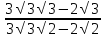 =
=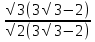 =
=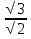 =
= 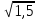 ;
;
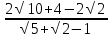 =
=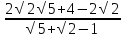 =
= 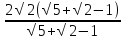 = 2
= 2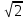 =
= 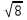 .
.
Ответ: 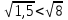 .
.
Итог урока. Рефлексия. Домашнее задание.
Сегодня мы рассмотрели некоторые способы преобразования выражений содержащих квадратные корни. Какие Далее учитель делает заключение о тех заданиях к которым нужно вернуться ориентируясь на «фигуренков» .
1
2 3
4
5 6
Литература.
1.Ю.Н.Макарычев, Н.Г.Миндюк « Алгебра » учебник для 8 класса общеобразовательных учреждений.
2.Л.И. Звавич, Л.В.Кузнецова «Дидактические материалы» Алгебра 8.
3.М.Ю.Шуба « Занимательные задания в обучении математике».
4.Издательский дом Первое сентября. Учебно- методическая газета « Математика» №12,1999 год.
