Министерство образования и науки Республики Казахстан
Атбасарский районный отдел образования
Акмолинской области
Открытый урок по алгебре в 9 классе
Арифметическая и геометрическая
прогрессии
подготовила учитель математики
высшей категории Исабекова Кульжаган Нурхамитовна
вечерняя сменная средняя общеобразовательная школа
г.Атбасар- 2014год
Тема: Арифметическая и геометрическая прогрессии и последовательности
( обобщающий урок)
Цели:
Образовательная:проверка уровня усвоения теоретических знаний и умения применять их при решении задач
Развивающая:развитие речи,умение правильно излагать свои мысли,анализировать и делать выводы
Воспитательная: воспитание интереса к предмету, потребности к знаниям
Тип урока:Урок обобщения и систематизации знаний
Организационные формы обучения: Групповая,
Оборудование: Интерактивная доска, карточки с заданиями
Видиоролик «Семь чудес света»
План урока:
1.Орг.момент
2.Мотивационное начало
3.Говорящая трибуна
4.Диктант
5.Составление и защита кластера
6.Решение задачи Магницкого
7.Индийская легенда
8.Самостоятельная работа по карточкам
9.Решение задач
10.Немного истории
11.Рефлексия
Ход урока
1.Организационный момент.
2. Мотивационное начало
Учащимся предлагаются обнаружить закономерность в таблице, заранее написанной на доске
| 4 | 8 | 16 | |
| 2 | 6 | 14 | |
| -2 | 4 | 12 | |
| -4 | -2 | 2 | 10 |
В первой строчке-геометрическая прогрессия
Во всех столбцах – арифметическая прогрессия
3 .Вступительное слово учителя: «Сегодня работаем по группам. Выбираем координатора группы. А в конце урока координаторы группы ставят себе оценки в таблицу и сдает учителю. » Работы оцениваются по «5» бальной системе
4. Повторение « Говорящая трибуна»
C каждой группы выходит один участник участники других групп задают вопросы
Слайд3
5. Математический диктант ( слайд 9)
Какая последовательность?
1) 2; 5; 8; 11;14; 17;…
2) 3; 9; 27; 81; 243;…
3) 1; 6; 11; 20; 25;…
4) –4; –8; –16; –32; …
5) 5; 25; 35; 45; 55;…
6) –2; –4; – 6; – 8;
Истинно или ложно высказывание Слайд 10
В арифметической прогрессии 2,4; 2,6;:: разность равна 2 .
2) В геометрической прогрессии 0,3; 0,9;:: третий член равен 2,7.
3) 11-й член арифметической прогрессии, у которой а1 = -4,2; d = 0,4, равен 0,2.
4) Сумма 5 первых членов геометрической прогрессии, у которой b1= 1 q = — 2, равна 11.
5) Последовательность чисел, кратных 5, является геометрической прогрессией.
6) Последовательность степеней числа 3 является арифметической прогрессией
6. Составление кластара слайд 10-11
1 группа арифметическая прогрессия
2 группа геометрическая прогрессия
3 группа последовательности
7.Защита кластара по группам
слайд 12
8.Решение задач из сборника Магницкого слайд 13
. Леонтий Филиппович Магницкий создатель первого учебника «Арифметика»
Некто продал лошадь за 156 рублей. Но покупатель, обретя лошадь, раздумал и возвратил продавцу, говоря: «Нет мне расчета покупать за эту цену лошадь, которая таких денег не стоит». Тогда продавец предложил другие условия:
«Если по-твоему цена лошади высока, то купи ее подковные гвозди, лошадь же получишь тогда в придачу бесплатно. Гвоздей в каждой подкове 6. За первый гвоздь дай мне 1/4 коп., за второй-1/2коп., за третий-1коп., и т.д.“
Покупатель, соблазненный низкой ценой, и желая даром получить лошадь, принял условия продавца, рассчитывая, что за гвозди придется уплатить не более 10 рублей.
Решение задачи слайд 14
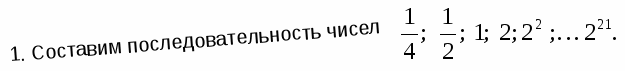
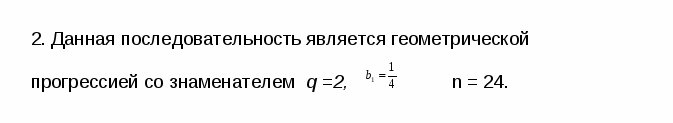
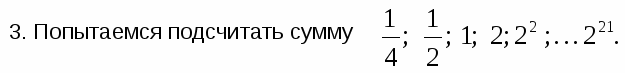
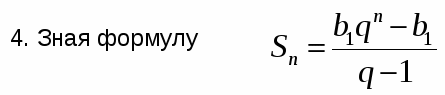
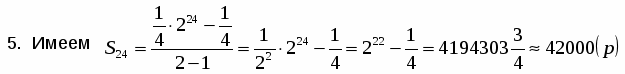
9.Задача о индийской легенде изобретения шахмат слайд 15-16
Ученик4. Изобретатель шахмат попросил в награду за свое изобретение столько пшеничных зерен, сколько их получится, если на первую клетку шахматной доски положить одно зерно, на вторую – в 2 раза больше (4 зерна), на третью еще в 2 раза больше (4 зерна) и т. д. до 64-ой клетки. Сколько зерен должен был получить изобретатель шахмат?
На доске запись: 1; 2; 4; 8; 16;…; ![]()
Учащиеся решают. ![]()
Учитель. Как велико это число? Кто может объяснить?
Ученик 1. Если бы удалось царю засеять пшеницей площадь всей поверхности Земли, считая и моря, и океаны, и горы, и пустыни, и Арктику с Антарктидой, и получить удовлетворительный урожай, то пожалуй, лет за пять смог бы рассчитаться. Чтобы поместить это зерно в амбаре, то его размеры будут: высота – 4м, ширина – 10м, длина – 30 000 000км – это вдвое больше, чем расстояние от Земли до Солнца.
Ученик 2. Математика – это точная наука. (На доске записывает число 18.446.744.073.709.551.615). читает: «18 квинтильонов 446 квадрильонов 744 триллиона 73 миллиарда 709 миллионов 551 тысяча 615.
Ученик 3. ![]() — так сказали бы современники Л.Ф. Магницкого.
— так сказали бы современники Л.Ф. Магницкого.
10.Работа по карточкам слайд17
Самостоятельная работа.
| q | n | bn | Sn | |
| 1 | 3 | 10 |
|
|
|
| ,5 | 8 | 2 |
|
| 2 |
| 7 | 1458 |
|
| ,5 |
|
| 1 | 12 |
| 128 | 12 |
| d | n | an | Sn | |
| 11 | -10 | 11 |
|
|
| 5 |
| 26 | 10 |
|
|
| 3 | 12 |
| 21 |
|
| 2 | 15 | -10 |
|
11.Решение задачи повышенной трудности
Задача из сборника заданий для экзамена
Какова сумма натуральных чисел:
Меньших 100 и не кратных 3?
Решение:
S1=1+2+…+99 S2=3+6+9+…+99
S1=(1+99)2 *99=4950
S2=(3+99)2*33=1683
S=S1-S2=4950-1683=3267
12.Каждый из команды решает по одной задаче у себя в тетради по усмотрению учителя можно вызвать некоторых учащихся к доске
Задания для команды №1.
Найдите семнадцатый член арифметической прогрессии: 19; 15;….
Найдите сумму первых семнадцати членов арифметической прогрессии: 19; 15;….
Найдите пятый член геометрической прогрессии ![]() , если
, если![]() .
.
Найдите сумму пяти первых членов геометрической прогрессии ![]() , если
, если ![]() .
.
-24; 12; -6;… — бесконечная геометрическая прогрессия. Найдите её сумму.
Задания для команды №2.
Найдите двадцать третий член арифметической прогрессии ![]() , если
, если ![]()
Найдите сумму первых двадцати трех членов арифметической прогрессии ![]() , если
, если ![]()
Найдите шестой член геометрической прогрессии ![]() , если
, если ![]()
Найдите сумму первых пяти членов геометрической прогрессии ![]() , если
, если ![]()
– 48; 24; — 12;… — бесконечная геометрическая прогрессия. Найдите её сумму.
Задания для команды №3.
1. Найдите пятнадцатый член арифметической прогрессии ![]() , если
, если ![]()
2. Найдите сумму первых пятнадцати членов арифметической прогрессии ![]() , если
, если ![]()
3. Найдите пятый член геометрической прогрессии ![]() , если
, если ![]() .
.
4. Найдите сумму первых пяти членов геометрической прогрессии ![]() , если
, если ![]() .
.
5. Найдите первый член бесконечной геометрической прогрессии, если ![]() .
.
Назад в историю слайд 18
Интересные факты слайд 19 .
Заключительное слово учителя
В течение урока мы повторили основные формулы арифметической и геометрической прогрессий. Показали применение этих формул в стандартных и нестандартных ситуациях
7. Рефлексия
| Формула n-го члена | Изменение последующего члена по отношению к предыдущему происходит на или в | Как это число найти | Как называется это число | Формула суммы n- первых членов | |
| Арифметическая прогрессия | | | | | |
| Геометрическая прогрессия | | | | | |
Данная стадия дает целостное осмысление, обобщение полученной информации
Личная карта команды
Карта оценивания
| Говорящая трибуна | Диктант | Формулы | кластер | Работа по карточкам | Решение задач | Доп. зад. | Количество баллов | Оценка | |
| 1 |
|
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
|
|
Используемая литература
1.Алгебра.Учебник для 9 класса Ю.Н.Макарычев
2.Алгебра Открытые уроки С.Н.Зеленская
3.Сборник заданий для проведения письменного экзамена за курс 9-летней общеобразовательной школы С.Н.Данилюк
4.Интернет-ресурс WWW. kopilka urokov.ru
