Открытый урок по алгебре в 9 классе
Тема: «Характеристическое свойство геометрической прогрессии»
Цели урока:
Образовательные: вспомнить и обобщить те знания, которые ученики уже имеют по геометрической прогрессии; активизировать работу по применению этих знаний; вывести и доказать характеристическое свойство геометрической прогрессии; приобрести умение по применению характеристического свойства при решении простых задач.
Развивающие: формировать умения наблюдать, подмечать закономерности, проводить рассуждение по аналогии, делать выводы на основе выявленных закономерностей, строить и интерпретировать модель некоторой реальной ситуации.
Воспитательные: содействовать воспитанию интереса к математике и ее приложениям, а также активности, умению аргументировано отстаивать свои взгляды.
Тип урока: комбинированный урок.
Структура урока
Подготовительный этап.
Актуализация знаний, умений и навыков.
Изучение нового материала.
Отработка знаний, умений и навыков по теме.
Решение задач практического содержания.
Подведение итогов урока и домашнее задание.
Ход урока
Подготовительный этап (3 мин.).
– Сегодня мы с вами выведем новое свойство геометрической прогрессии.
– Но сначала проверим домашнее задание.
Один ученик вызывается к доске и записывает определение геометрической прогрессии, формулу n-го члена геометрической прогрессии и формулу суммы n первых членов геометрической прогрессии.
С остальными учениками проверяем выполнение домашнего задания, опрашивая с места ответы в домашних заданиях.
№17.25 (а, в) а)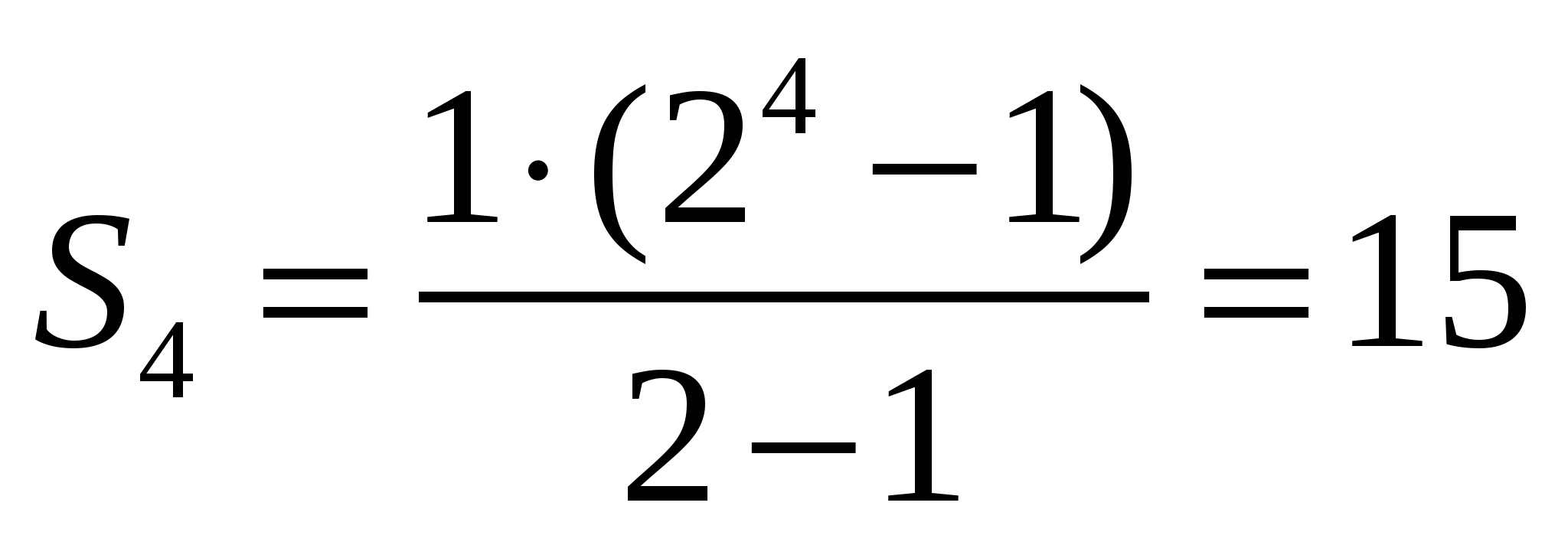 ; в)
; в)
№17.27 (а, б) а) 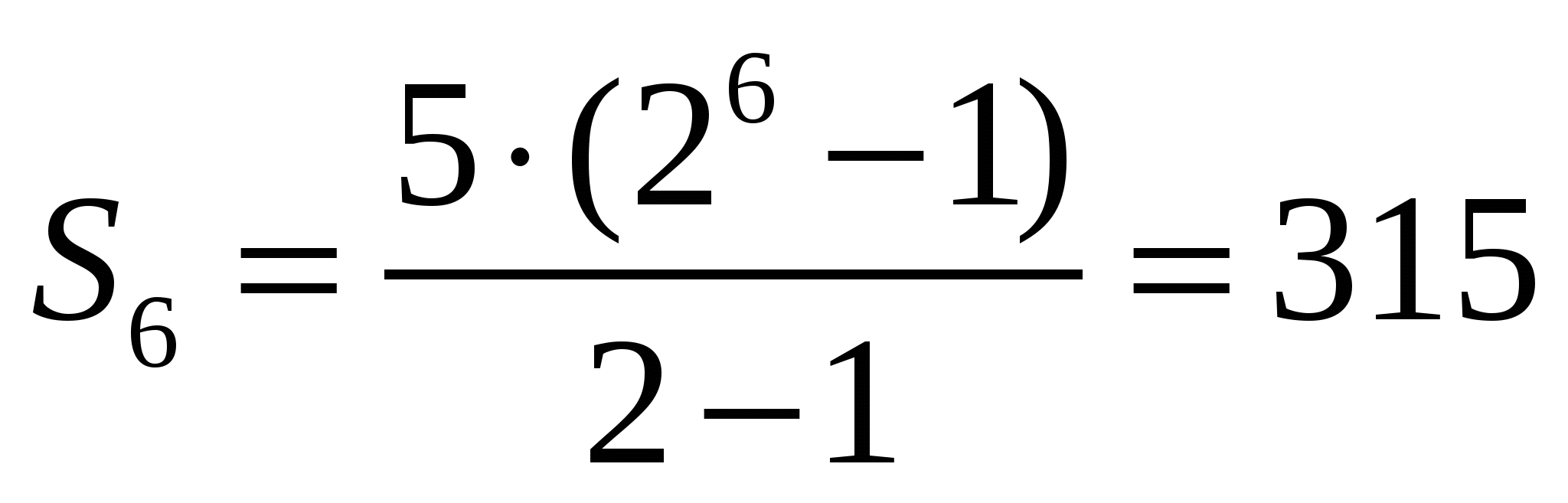 ; б)
; б) 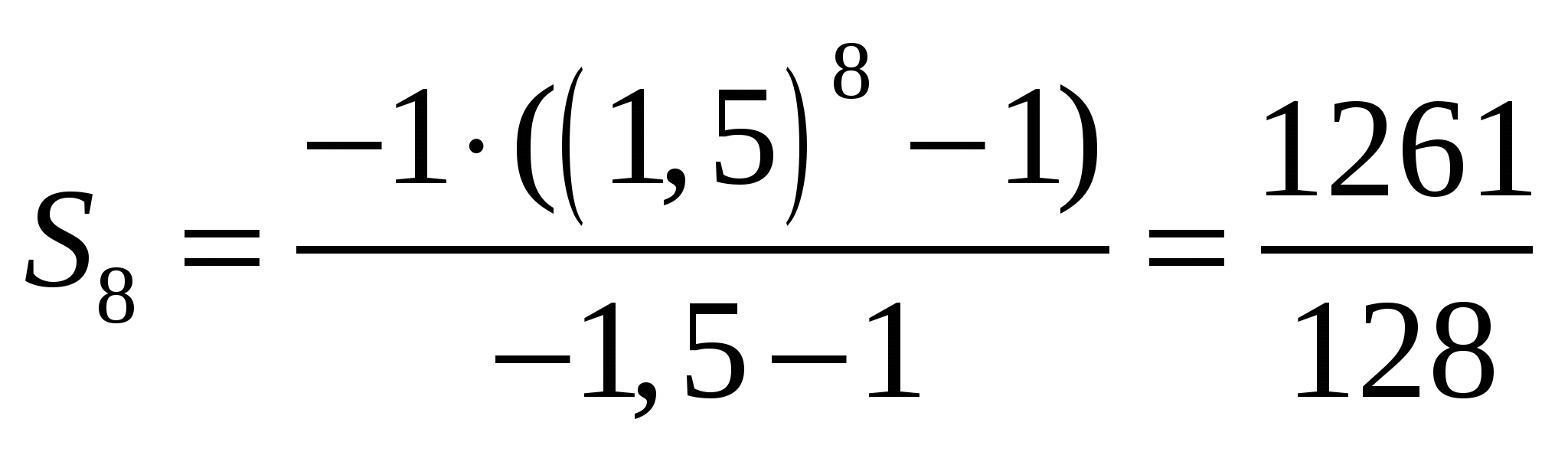
№17.28 (а, в) а) 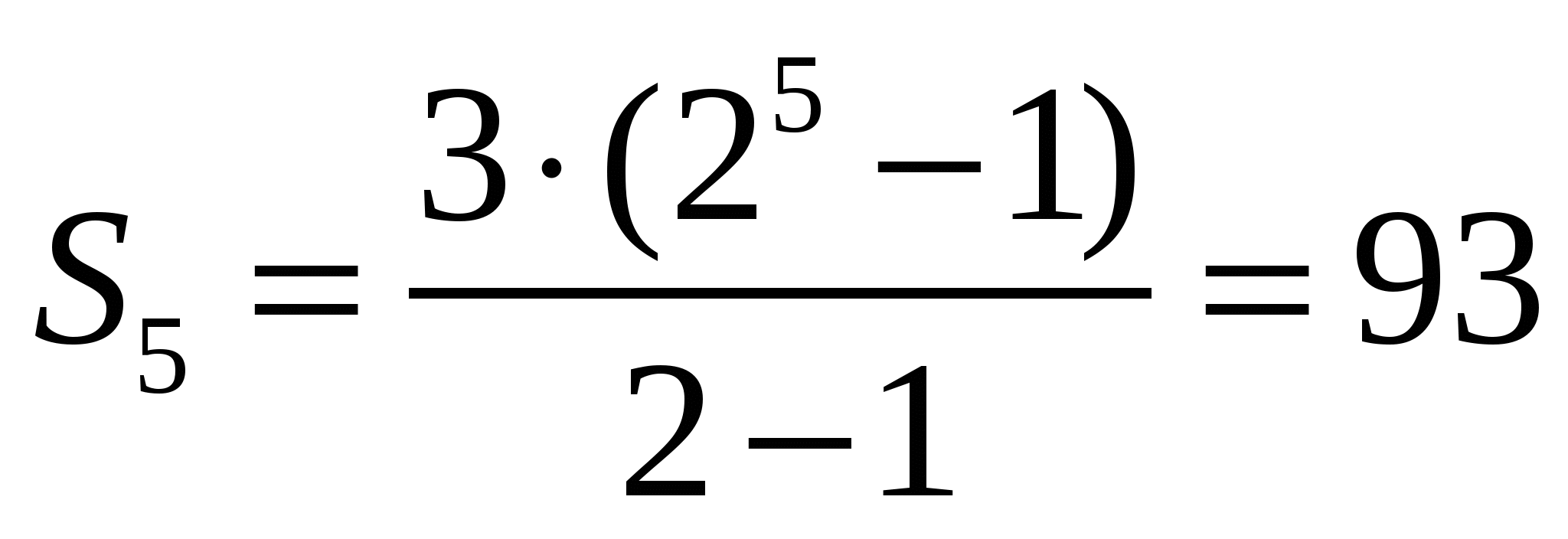 ; в)
; в) 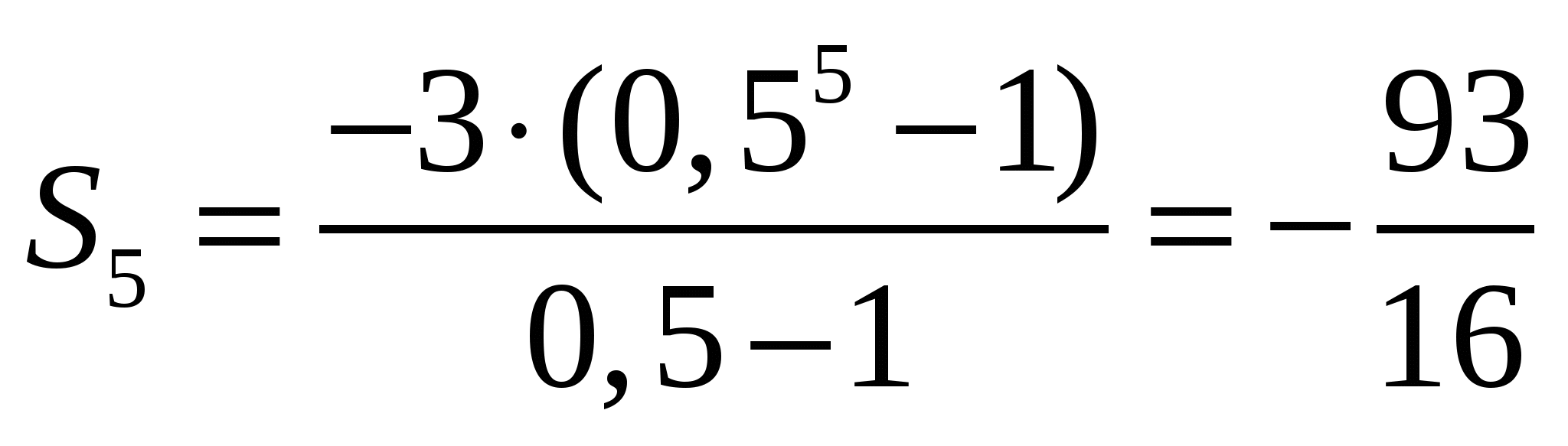
№17.29 (а, в) а) 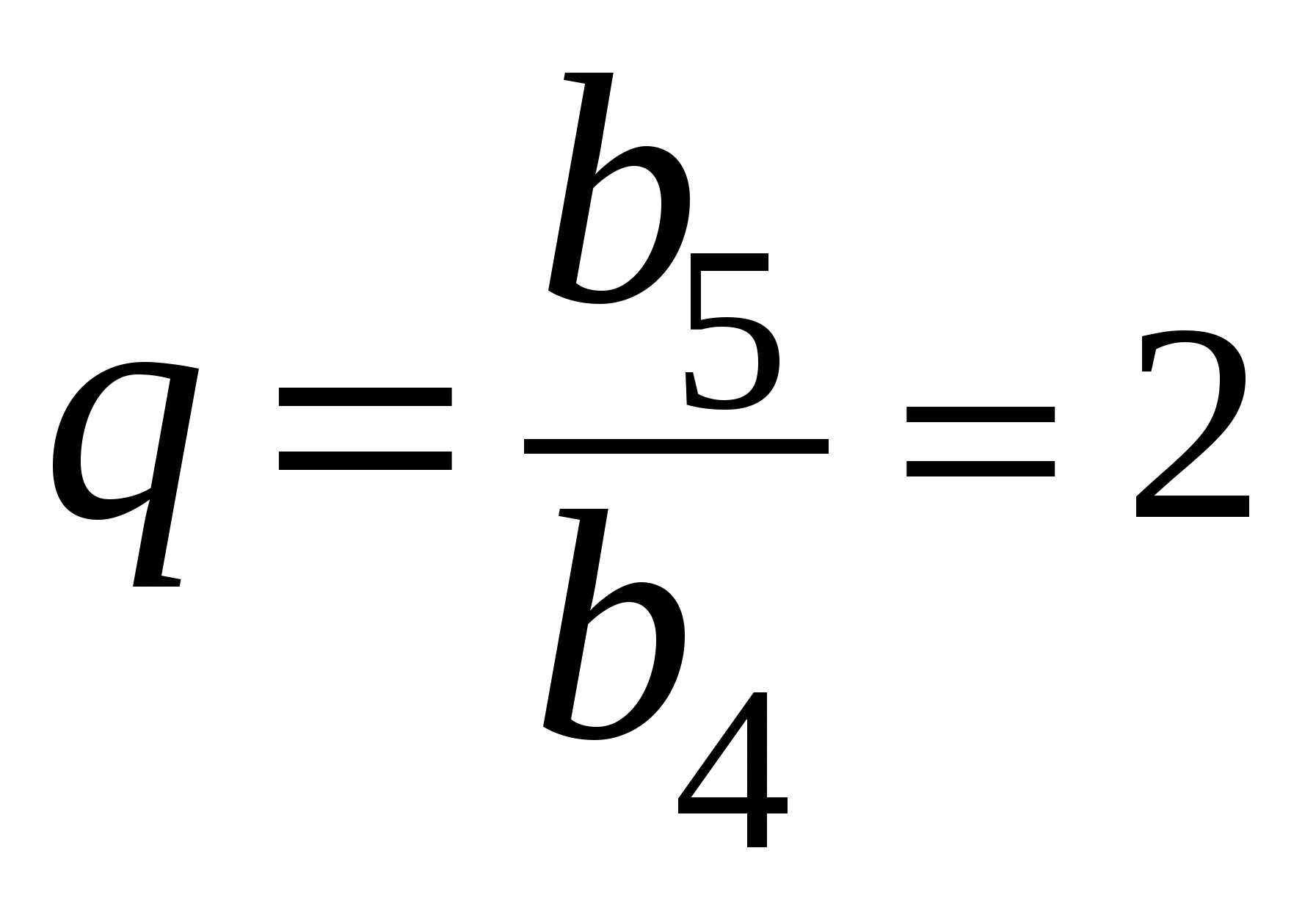 ,
, 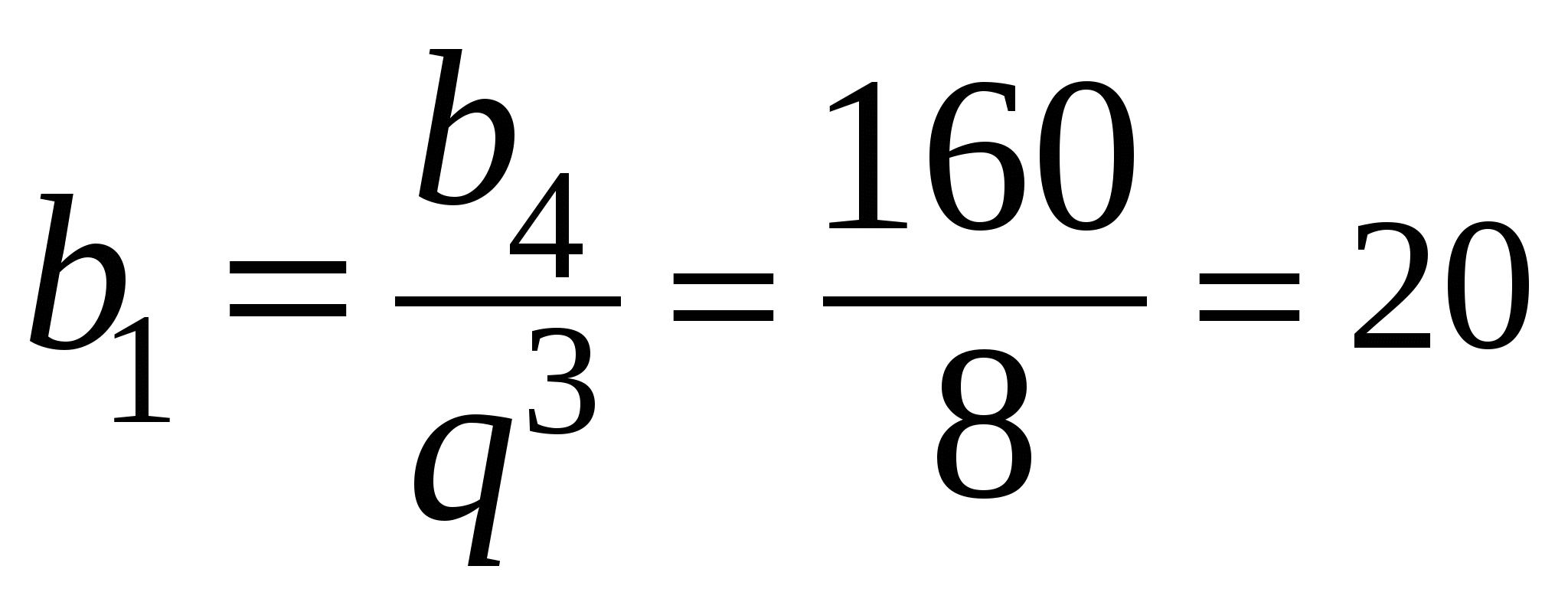 ,
, 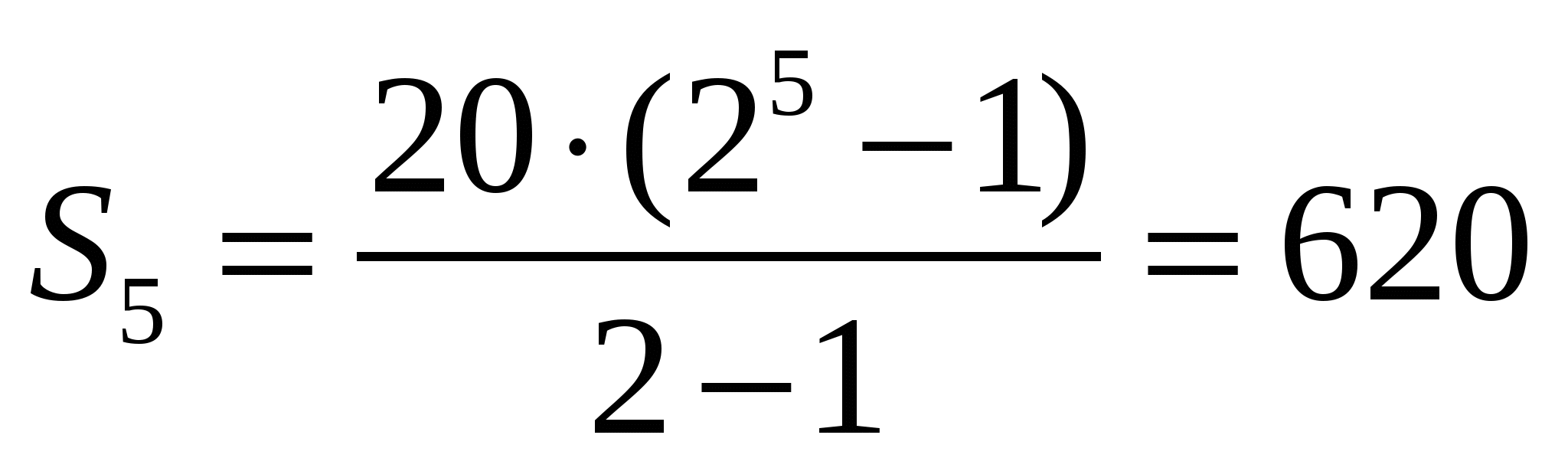
в)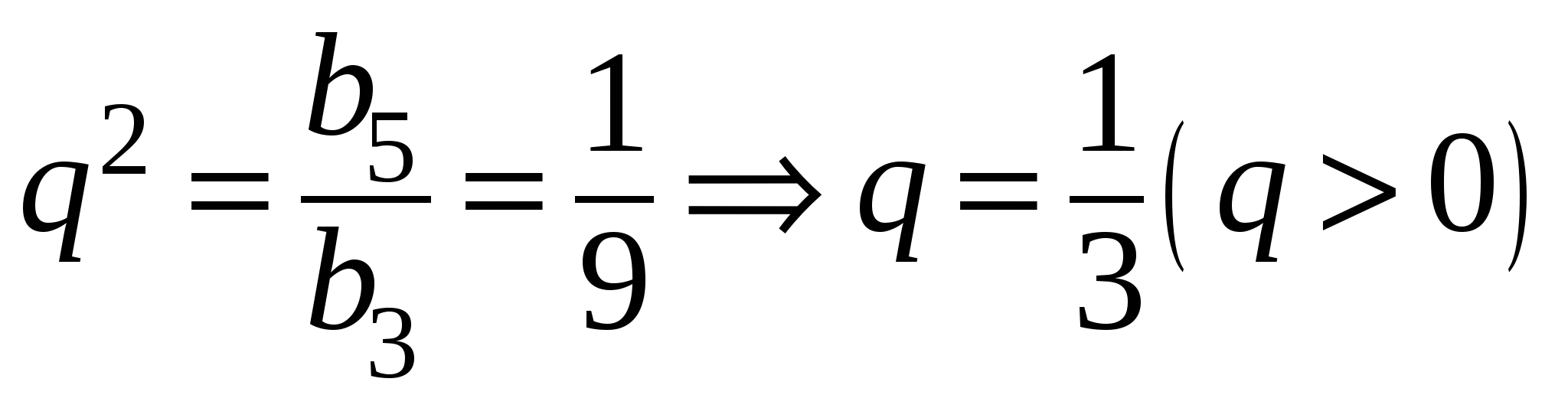 ,
, 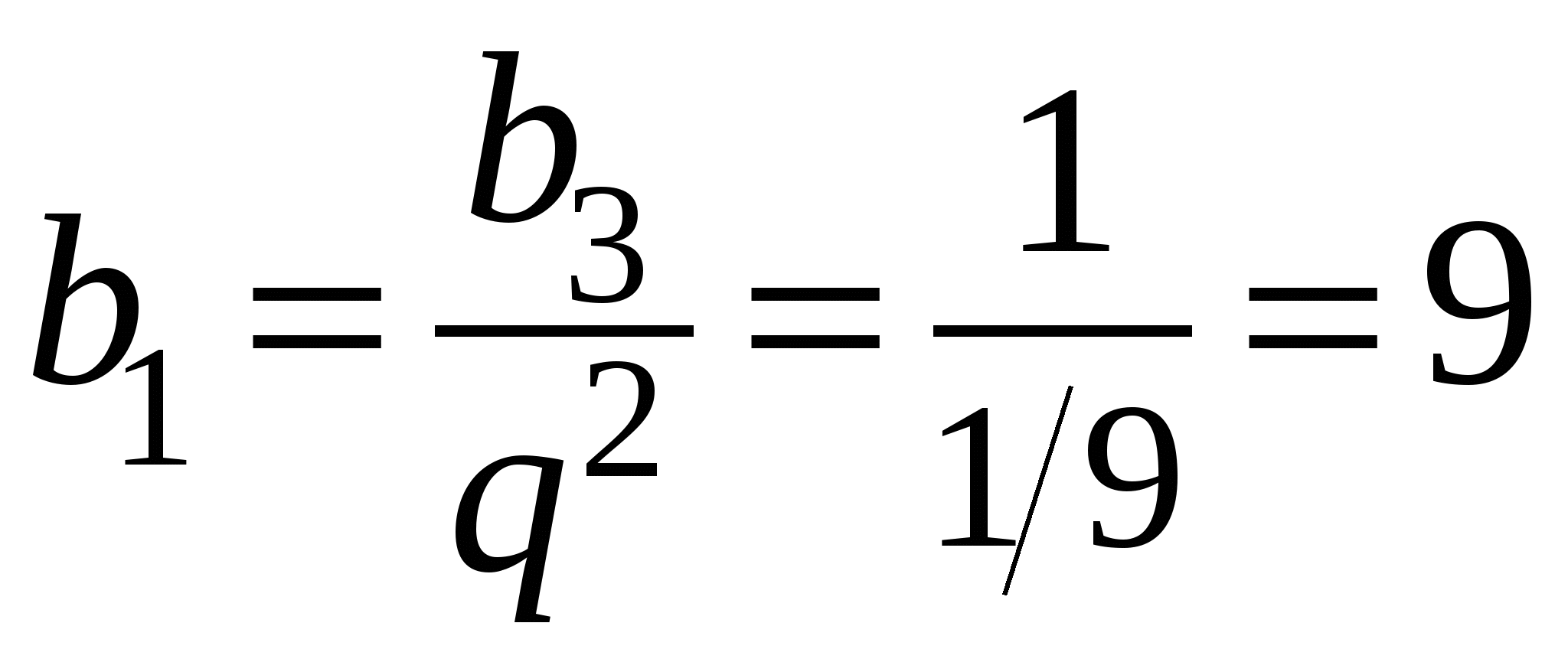 ,
,

Актуализация знаний, умений и навыков (7 мин.).
– Чтобы вспомнить все, что вы знаете о геометрической прогрессии, проведем устную работу по карточкам. Будут работать две группы: группа девочек и группа мальчиков.
Каждой группе выдаются карточки с выбором ответа. После выполнения заданий в каждой группе должно получиться свое слово.
| Карточка №1 |
| |||
| Найдите знаменатель геометрической прогрессии, если | ||||
| М. 2 | Б. | Х. –2 | Г. 0,5 | |
Ответ: Х
| Карточка №2 |
| |||
| Найдите первый член геометрической прогрессии, если | ||||
| Н. 12 | А. 3 | Ч. 6 | О. 1,5 | |
Ответ: А
| Карточка №3 |
| |||
| Найдите четвертый член геометрической прогрессии, если | ||||
| М. 54 | Е. 81 | Л. 162 | К. –54 | |
Ответ: К
| Карточка №4 |
| |||
| Найдите знаменатель геометрической прогрессии, если | ||||
| Р. 2 | Б. –4 | Ф. 4 | В. –2 | |
Ответ: Р
| Карточка №5 |
| |||
| Найдите сумму четырех первых членов геометрической прогрессии, если | ||||
| К. –160 | Т. –80 | У. –26 | Г. 80 | |
Ответ: Т
| Карточка №6 |
| |||
| Найдите пятый член геометрической прогрессии, если | ||||
| И. 8 | Ю. 40 | Е. 4 | А. 2 | |
Ответ: Е
| Карточка №1 |
| |||
| Найдите знаменатель геометрической прогрессии | ||||
| У. –3 | С. | Т. | А. 3 | |
Ответ: С
| Карточка №2 |
| |||
| Найдите первый член геометрической прогрессии, если | ||||
| В. –2 | Б. | Ч. 6 | Г. 2 | |
Ответ: В
| Карточка №3 |
| |||
| Найдите четвертый член геометрической прогрессии, если | ||||
| Е. 24 | А. –48 | Й. –24 | И. 48 | |
Ответ: Й
| Карточка №4 |
| |||
| Найдите знаменатель геометрической прогрессии, если | ||||
| Ю. 3 | Б. –9 | У. 9 | О. –3 | |
Ответ: О
| Карточка №5 |
| |||
| Найдите сумму четырех первых членов геометрической прогрессии, если | ||||
| М. –21 | Т. –85 | Б. –255 | Д. 85 | |
Ответ: Т
1 группа
Под числом, соответствующим номеру задания, напишите букву.
| 2 | 4 | 2 | 3 | 5 | 6 | 4 | |
|
|
|
|
|
|
|
|
|
Должно получиться слово ХАРАКТЕР.
2 группа
Под числом, соответствующим номеру задания, напишите букву.
| 2 | 4 | 3 | 1 | 5 | 2 | 4 | |
|
|
|
|
|
|
|
|
|
Должно получиться слово СВОЙСТВО
Примечание:
Если будут присутствовать все ученики, то 1 группа – 4 девочки, 2 – группа – 3 мальчика.
Если не будет 1 девочки, то в группе девочек исключить Карточку №6, а букву в бланк написать учителю.
Карточки с заданием можно раздать с учетом уровня знаний ученика.
– В результате работы в 1 группе получилось слово Характер. По словарю Сергея Ивановича Ожегова характер – это отличительное свойство, качество, особенность кого-либо (чего-либо).
– Итак, сегодня мы с вами выведем еще одно свойство геометрической прогрессии – характеристическое свойство.
Изучение нового материала (14 мин.).
– Вам известно характеристическое свойство арифметической прогрессии, попробуем определить характеристическое свойство для геометрической прогрессии.
Рассмотрим последовательность чисел, являющуюся геометрической прогрессией
![]() : 1, 2, 4, 8, 16, 32, …
: 1, 2, 4, 8, 16, 32, …
Выполните задания:
Найдите произведение членов этой прогрессии:
| = 4 | |
| с номерами 2 и 4 | = 16 |
| с номерами 3 и 5 | = 64 |
Сравните полученное произведение с тем членом прогрессии, который находится между ними:
сравнить 4 и 2
сравнить 16 и 4
сравнить 64 и 8
– Какая закономерность существует?
– Произведение ![]() и
и ![]() равно квадрату
равно квадрату ![]()
– Произведение ![]() и
и ![]() равно квадрату
равно квадрату ![]()
– Произведение ![]() и
и ![]() равно квадрату
равно квадрату ![]()
– В результате получили формулу…
– ![]() для
для ![]()
– Это свойство геометрической прогрессии называется характеристическим. Оно формулируется так: «Квадрат каждого члена геометрической прогрессии, кроме первого, равен произведению предыдущего и последующего членов».
– Докажем это свойство:
![]() (по определению геометрической прогрессии для
(по определению геометрической прогрессии для ![]() )
) ![]()
![]() (по определению геометрической прогрессии)
(по определению геометрической прогрессии)
Перемножим ![]() и
и ![]() , получим:
, получим:
![]() для
для ![]()
– Верно и обратное: если последовательность ![]() , состоящая из чисел, отличных от нуля, такова, что для любого
, состоящая из чисел, отличных от нуля, такова, что для любого ![]() выполняется равенство
выполняется равенство ![]() , то
, то ![]() – геометрическая прогрессия.
– геометрическая прогрессия.
– Доказательство этого утверждения разберите дома самостоятельно по учебнику стр. 166 – 167.
Отработка знаний, умений и навыков по теме (7 мин.).
№17.16 (а) – на доске учитель, ученики помогают.
а) Между числами 18 и 2 вставьте положительное число так, чтобы получилось три последовательных члена геометрической прогрессии.
– Из трех последовательных членов геометрической прогрессии известны первый и третий члены. Найти нужно второй член.
Дано:
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Найти: ![]()
Решение.
![]() (характеристическое свойство)
(характеристическое свойство)
![]()
![]() или
или ![]()
Так как по условию ![]() , то
, то ![]() – не подходит.
– не подходит.
Ответ: ![]()
№17.31 (б) – ученики самостоятельно.
б) Между числами 18 и 2 вставьте положительное число так, чтобы получилось три последовательных члена геометрической прогрессии.
Дано:
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Найти: ![]() ,
, ![]()
Решение.
1) ![]() (характеристическое свойство)
(характеристическое свойство)
![]()
![]() или
или ![]()
Так как по условию ![]() , то
, то ![]() .
.
2) 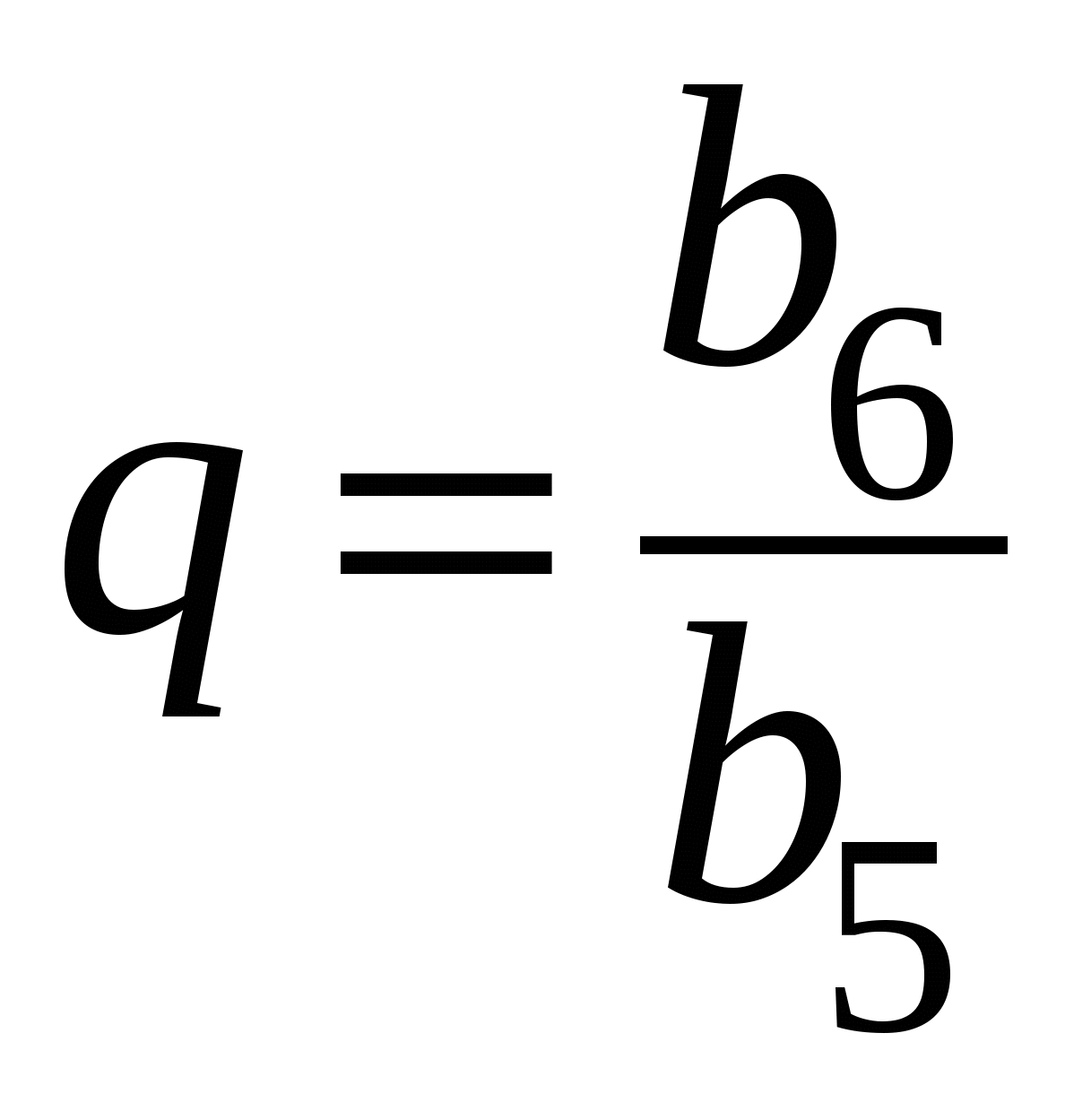 (по определению)
(по определению)
![]()
![]()
Ответ: ![]() ,
, ![]()
№17.32 – вызвать к доске.
Найдите те значения t, при которых числа t, 4t, 8 являются последовательными членами геометрической прогрессии.
Дано:
![]() : t, 4t, 8
: t, 4t, 8
Найти: t
<p