







 Поурочные планы по разделу «Теория вероятностей
Поурочные планы по разделу «Теория вероятностей
и математическая статистика» по алгебре 9 класса
Урок №1
Тема: Понятие о теории вероятностей и математической статистике.
Цели урока: — познакомить учащихся 8-го класса с основными понятиями теории вероятности;
— уметь приводить примеры случайных событий.
-понимать, что вероятность – числовая мера правдоподобия события, что вероятность – число, заключенное в пределах от 0 до 1.
— способствовать развитию интереса к математике; умений применять новый материал на практике и в жизни
— способствовать воспитанию аккуратности;
Новые понятия: Событие, достоверные события, случайные события, невозможные события, частота случайного события.
Оборудование: доска.
Тип урока: изучение нового материала.
План урока:
| 5 мин. | |
| Актуализация | 5 мин. |
| Мотивация | 2 мин. |
| Объяснение нового материала | 15 мин. |
| Первичное осмысление и закрепление | 5 мин. |
| Решение задач | 10 мин. |
| Подведение итогов | 2 мин. |
| Домашнее задание | 1 мин. |
Ход урока:
1. Вступительное слово учителя.
Случай, случайность – с ними мы встречаемся повседневно: случайная встреча, случайная поломка, случайная находка, случайная ошибка. Этот ряд можно продолжать бесконечно. Также в обыденной жизни мы часто говорим «возможно», невозможно», « вероятно», маловероятно», « обязательно». Подобные выражения обычно используются, когда мы говорим о возможностях наступления какого-либо события или явления. С такими событиями мы встречаемся очень часто, но не всегда их замечаем. Казалось бы, тут нет места для математики,– какие уж законы в царстве Случая! Но и здесь наука обнаружила интересные закономерности – они позволяют человеку уверенно чувствовать себя при встрече со случайными событиями.
Немного истории о возникновении теории вероятности ( см. приложение1)
Основные понятия теории вероятности:
Определение: Теория вероятностей – это раздел математики, изучающий вероятно- статистические закономерности.
Например, с помощью данной теории можно посчитать вероятность того, что конкретного ученика в классе вызовут к доске на уроке.
На основе теории вероятностей возникла специальная наука – математическая статистика.
Статистика –наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе. Слово « статистика» происходит от латинского слова status, которое означает « состояние, положение вещей»
Статистика знает всё!
Известно, сколько, какой пищи съедает в год в среднем гражданин республики. Сколько в стране охотников, балерин, артистов, рабочих и т. д.
Результаты статистических исследований широко используются для практических и научных выводов. Статистические характеристики применяют для нахождения средней урожайности пшеницы с 1 га в данном районе, среднего суточного удоя молока от одной коровы на ферме и т.д
Рассмотрим основные понятия теории вероятности.
Теория вероятности, как и любой, раздел математики, оперирует определённым кругом понятий. Большинству понятий теории вероятностей даются определения, но некоторые принимаются за первичные, не определяемые, как в геометрии точка, прямая, плоскость. Первичным понятием теории вероятностей является событие. Под событием понимают то, относительно чего после некоторого момента времени можно сказать одно и только одно из двух:
Да, оно произошло.
Нет, оно не произошло.
Например, у меня есть лотерейный билет. После опубликования результатов розыгрыша лотереи интересующее меня событие – выигрыш тысячи рублей либо происходит, либо не происходит. Любое событие происходит вследствие испытания (или опыта). Под испытанием (или опытом) понимают те условия, в результате которых происходит событие. Например, подбрасывание монеты – испытание, а появление на ней “герба” – событие. Событие принято обозначать заглавными латинскими буквами: A,B,C,… . События в материальном мире можно разбить на три категории – достоверные, невозможные и случайные.
Определение: Случайные события – это события, которые при одних и тех же условиях могут произойти, а могут и не произойти.
Например, случайным событием является солнечная погода.
В обычном понимании вероятностью называют количественную оценку возможности наступления ожидаемого события.
Определение: События, которые в данных условиях произойти не могут, называются невозможными.
Например, то, что последний день зимы придется на 30 февраля.
Определение: События, которые в данных условиях обязательно происходят, называются достоверными.
Например, окончание урока.
Итак, достоверное событие – это событие, наступающее при данных условиях со стопроцентной вероятностью (т.е. наступающее в 10 случаях из 10, в 100 случаях из 100 и т.д.). Невозможное событие – это событие, не наступающее при данных условиях никогда, событие с нулевой вероятностью.
Но, к сожалению (а может быть, и к счастью), не все в жизни так четко и ясно: это будет всегда (достоверное событие), этого не будет никогда (невозможное событие). Чаще всего мы сталкиваемся именно со случайными событиями, одни из которых более вероятны, другие менее вероятны. Обычные люди используют слова “более вероятно” или “менее вероятно”, как говорится, по наитию, опираясь на то, что называется здравым смыслом. Но очень часто такие оценки оказываются недостаточными, поскольку бывает важно знать, на сколько процентов вероятно случайное событие или во сколько раз одно случайное событие вероятнее другого. Иными словам, нужны точные количественные характеристики, нужно уметь охарактеризовать вероятность числом.
Первые шаги в этом направлении мы с вами уже сделали. Мы говорили, что вероятность наступления достоверного события характеризуется как стопроцентная, а вероятность наступления невозможного события – как нулевая. Учитывая, что 100% равно 1, люди договорились о следующем:
1) вероятность достоверного события считается равной 1;
2) вероятность невозможного события считается равной 0.
А как подсчитать вероятность случайного события? Ведь оно произошло случайно, значит, не подчиняется закономерностям, алгоритмам, формулам. Оказывается, и в мире случайного действуют определенные законы, позволяющие вычислять вероятности. Этим занимается раздел математики, который как мы уже сказали, и называется – теория вероятностей.
В практической жизни мы сталкиваемся с различными случайными событиями, причём они происходят с разной частотой: одни чаще, другие реже.
Например: бросаем игральную кость 48 раз и составим таблицу, в которой указаны числа выпадений каждого из цифр: 1,2, 3, 4, 5, 6.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Число выпадений | 6 | 8 | 9 | 7 | 8 | 10 |
По данным таблицы построим столбчатую диаграмму:
6
6 8 9 7 8 10
Определение: Отношение частоты появления некоторого события к общему числу событий называют вероятностью события.
Вероятность появления ( выпадения) цифры 5 при бросании игральной кости 48 раз равна  .
.
Рассмотрим примеры на закрепление материала:
Задание 1.
Какие из следующих событий – случайные, достоверные, невозможные:
1)черепаха научиться говорит;
2)вода в чайнике, стоящим на горячей плите закипит;
3)ваш день рождения – 19 октября
4)день рождение вашего друга – 30 февраля;
5)вы выиграете ,участвуя в лотереи;
6)вы не выигрываете, участвуя в беспроигрышной лотереи;
7)вы проиграете партию в шахматы;
8)на следующей недели испортиться погода;
9)вы нажали на звонок, а он не зазвонил;
10)после четверга будет пятница;
11)после пятницы будет воскресенье.
Задание 2.
Для каждого из перечисленных событий определите, какое оно: достоверное, возможное, невозможное
1)летом у школьников будут каникулы;
2)1 июня в День защиты детей будет солнечно;
3)после уроков дежурные уберут кабинет;
4)в 11-м классе школьники не будут изучать алгебру;
5)зимой выпадает снег;
6)при включении света, лампочка перегорит;
7)вы выходите на улицу, а на встречу вам идет слон
Решить задачи по учебнику: № 322, №323 ( с последующей проверкой)
Подведение итогов:
Что такое событие?
Какое событие называют действительным?
Какое событие называют случайным?
Какое событие называют невозможным?
Какие ученые занималась поиском закономерностей в случайных событиях?
Домашнее задание: п. 17, № 320, 321,
Разбить учеников на тройки. Каждая тройка пишет реферат на одну из тем:
Даниил Бернулли и его вклад в развитие теории вероятностей.
Гюйгенс и его вклад в развитие теории вероятностей
Блез Паскаль и его вклад в развитие теории вероятностей
Ферма и его вклад в развитие теории вероятностей.
Приложение1.
Как наука теория вероятности зародилась в 17в. Возникновение понятия вероятности было связано как с потребностями страхования, получившего значительное распространение в ту эпоху, когда заметно росли торговые связи и морские путешествия, так и в связи с запросами азартных игр.
Слово “азарт”, под которым обычно понимается сильное увлечение, горячность, является транскрипцией французского слова hazard, буквально означающего “случай”, “риск”. Азартными называют те игры, а которых выигрыш зависит главным образом не от умения игрока, а от случайности.
Схема азартных игр была очень проста и могла быть подвергнута всестороннему логическому анализу. Первые попытки этого рода связаны с именами известных учёных – алгебраиста Джероламо Кардано (1501 – 1576) и Галилео Галилея (1564 – 1642). Однако честь открытия этой теории, которая не только даёт возможность сравнивать случайные величины, но и производить определенные математические операции с ними, принадлежит двум выдающимися ученым – Блезу Паскалю (1623 – 1662) и Пьеру Ферма. Ещё в древности было замечено, что имеются явления, которые обладают особенностью: при малом числе наблюдений над ними не наблюдается никакой правильности, но по мере увеличения числа наблюдений всё яснее проявляется определенная закономерность. Всё началось с игры в кости.
Азартные игры практиковались в ту пору главным образом среди знати, феодалов и дворян. Особенно распространенной была игра в кости. Было замечено. что при многократном бросании однородного кубика, все шесть граней которой отмечены соответственно числами 1, 2, 3, 4, 5, 6 число очков от 1 до 6 выпадают в среднем одинаково часто, иными словами, выражаясь языком математики, выпадение определённого числа очков имеет вероятность, равную 1/6 (т.е. отношению числа случаев, благоприятствующих событию к общему числу всех случаев). Аналогично вероятность появления на верхней грани кости чётного числи очков равна 3/6 ,так как из шести равновозможных случаев чётное число появляется только в трёх.
Решение порой довольно сложных задач, с которыми обращались заинтересованные лица к Паскалю, Ферма, Гюйгенсу, способствовало разработке основных понятий и общих принципов теории вероятностей, в том числе и правил действия над ними. Отсюда не следует, конечно, заключать, что основоположники теории вероятностей рассматривали азартные игры как единственный или главный предмет разрабатывавшейся ими новой отрасли науки.
На развитие теории вероятностей оказали влияние более серьёзные потребности науки и запросы практики, в первую очередь страховое дело, начатое в некоторых странах ещё в 16в. В 16-17вв. учреждение страховых обществ и страхование судов от пожара распространились во многих европейских странах.
Азартные игры были для ученых только удобной моделью для решения задач и анализа понятий теории вероятности. Об этом заметил ещё Гюйгенс в своей книге “О расчётах в азартной игре” (1657), которая была первой книгой в мире по теории вероятностей. Он писал: “…при — внимательном изучении предмета читатель заметит, что он занимается не только игрой, а что здесь даются основы глубокой и весьма интересной”. Гюйгенс впервые ввёл важное для теории вероятностей понятие математического ожидания, которое получило дальнейшее развитие а трудах Даниила Бернулли, Даламбера и др. Понятие математического ожидания находит немало применений а разных других областях человеческой деятельности.
Таким образом, в 60-е годы 17в. были выработаны первые понятия и некоторые элементы теории вероятностей. В последующие два века учёные столкнулись с множеством новых задач, связанных с исследованием случайных явлений.
Урок №2
Тема: Понятие о теории вероятностей и математической статистике.
Цели урока:
Образовательные: -Сформулировать правило вычисления вероятностей.
Развивающие: -Развивать внимание, логическое мышление, самостоятельность мышления.
Воспитательные-: Формировать качества личности: организованность, аккуратность.
Оборудование к уроку:
Игральные кубики на каждом столе.
Монеты у каждого ученика.
Ход урока
I. Актуализация опорных знаний и умений
а) Вопросы к классу:
1) Что мы называем случайным событием?
2) Приведите примеры возможных случайных событий.
3) Что называют вероятностью события?
4) Какие события называем достоверными, невозможными, случайными?
5) Приведите примеры достоверного события и невозможного события.
Учитель: Один из основателей математической статистики, шведский ученый Харальд Крамер писал: «По – видимому, невозможно дать точное определение того, что подразумевается под словом «случайный». Смысл этого слова лучше всего разъяснить на примерах». И мы последуем этому совету.
б) У вас на столах лежат игральные кубики. Подбросьте два кубика. Посмотрите какие события произойдут.
А теперь внимание на доску. (На доске записано задание.)
А = {на кубиках выпало одинаковое число очков}
В = {сумма очков на кубиках не превосходит 12}
С = {сумма очков на кубиках равна 11}
Д = {произведение очков на кубиках равно 11}
Вместе обсудить какие события являются случайными, какие достоверными, а какие невозможными (А; С – случайные; В – достоверное; Д — невозможное)
в) Рассмотрим задачу:
В коробке лежат 3 красных, 3 желтых, 3 зеленых шара. Вытаскиваем наугад 4 шара. Какие из следующих событий невозможны, какие случайны, а какие достоверны?
(На доске записано )
А = {все вынутые шары одного цвета}
В = {все вынутые шары разных цветов}
С = {среди вынутых шаров есть шары разных цветов}
Д = {среди вынутых шаров есть шары всех трех цветов}
Учащиеся выполняют это задание самостоятельно 2-3 мин.
По окончании работы проверить результаты (А и В невозможные, С – достоверное, Д — случайное).
II. Формирование знаний и умений учащихся.
Учитель: Говоря о достоверном событии, мы не будем применять слово «вероятно». Вряд ли мы скажем: «Вероятно, завтра будет четверг». Для невозможного события, мы могли бы сказать: «Уверен, что завтра не пятница», или «вероятность того, что завтра пятница нуль».
В жизни мы чаще сталкиваемся со случайными событиями. В этом случае мы используем слова «более вероятно», «менее вероятно».
А как подсчитать вероятность случайного события? Ведь оно произошло случайно, значит, не подчиняется закономерностям. Оказывается, и в мире случайного действуют определенные законы.
Этим занимается раздел математики о котором мы с говорили на прошлом уроке(«теория вероятностей»)
Задание для всего класса: Возьмите в руки кубики.
При бросании кубика, сколько различных элементарных событий может произойти? (6)
Сколько событий благоприятных событию «выпадет 4»? (1)
Сформулируем правило:
Число всех возможных исходов – N
Все исходы равновозможны
Количество благоприятных исходов – N(A)
P(A) – вероятность события А
P(A) = ![]()
Задача :
Бросают одну игральную кость. Вычислить вероятность события «выпало четное число очков».
Решение: N = 6; N(A) = 3; P(A) = 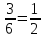 .
.
Самостоятельная работа:
№1 Для каждого из следующих событий введите число всех возможных исходов, число благоприятных исходов и вероятность.
а) В урне 5 белых и 15 черных шаров, из урны наугад вынимается два шара. Какова вероятность того, что они будут белыми?
б) Из русского алфавита случайным образом выбирается одна буква. Какова вероятность того, что она окажется согласной?
в) Из слова ВЕРОЯТНОСТЬ случайным образом убирается одна буква. Какова вероятность того, что она окажется гласной?
№2 Определить вероятности следующих событий:
A={при бросании монеты выпал «орел»};
B={при бросании кубика выпала тройка};
C={при бросании кубика выпало четное число};
D={из колоды карт вытянули туза };
E={из колоды карт вытянули шестерку};
F={из колоды карт вытянули не туза};
Ответы проверяются учителем.
I I I. Подведение итогов урока: выставление оценок
IV. Домашнее задание: п.17 № 324, 325.
Повторить к следующему уроку такие понятия: мода, размах, среде арифметическое.
Урок № 3
Тема: Группировка и анализ статистических данных.
Цели урока:
Обучающие, развивающие:
-познакомить с начальными представлениями о сборе и группировке статистических данных, составлением таблиц частот и относительных частот;
знать основные статистические характеристики описательной статистики (среднее арифметическое, размах, моду и медиану);
уметь производить сбор и группировку статистических данных;
сформировать навыки по обработке статистической информации;
-рассмотреть различные способы наглядного изображения результатов статистических исследований.
Воспитательные:
способствовать формированию коммуникативной компетенции учащихся;
— развивать самостоятельность и навыки самоконтроля.
Оборудование:
