Решение логарифмических уравнений, 10-11 класс

Муниципальное бюджетное образовательное учреждение

дополнительного образования детей дом детского творчества

г.Зверева Ростовской области.

Муниципальное бюджетное образовательное учреждение

средняя образовательная школа №1

г.Зверева Ростовской области.

«Решение логарифмических уравнений»

Работа педагога дополнительного

образования МБОУ ДОД ДДТ,

учителя математики МБОУ СОШ №1

Куца Фёдора Ивановича

г. Зверево

2013г

Содержание работы:

1) Уравнения вида log _a x = b.

2) Уравнения вида log _a f (x) = b.

3) Уравнения вида log _a f (x) = g(x).

4) Уравнения вида log _a f (x) = log _a g (x).

5) Уравнения вида log _a(x) f(x) = log _a(x) g(x).

6) Уравнения вида log _a (log _b f (x)) = c.

7) Замена переменной.

8) Приведение к одному основанию.

9) Уравнения с неизвестным в основании логарифма

10) Уравнения вида log _a f (x)∙log _b g(x) = 0.

11) Разложение на множители левой части уравнения.

12) Использование формулы перехода к новому основанию.

13) Использование формулы log _a b + log _a c = log _a (bc).

14) Использование формулы log _a b — log _a c = log _a (b/c)

15)Уравнения вида A∙( log _a f (x))² + B∙ log _a f (x) + C = 0 .

16) Показательно — логарифмические уравнения.

17) Использование однородности.

18) Уравнения вида = g(x).

19) Уравнения вида = b.

20) Уравнения вида = g(x).

21) Использование формул log _a (b/c) = log _a |b| — log _a |c|, log _a(b∙c) = log _a |b| + log _a |c|.

22) Использование формулы log _f(x) (g(x))ⁿ = n∙ log _f(x) |g(x)| (При четном n).

23) Рационально – логарифмические уравнения

24) Иррационально – логарифмические уравнения

25) Уравнения, содержащие модуль.

26) Комбинированные уравнения.

27) Оценочная «граничная» задача.

28) Использование монотонности функций.

1) Уравнения вида log _a x = b.

Уравнение вида log _a x = b при всех допустимых a имеют единственное решение x = a ^b.

Пример. log ₃ x= 4.

х = 3⁴,

х = 81.

Ответ. х = 81.

2) Уравнения вида log _a f (x) = b.

Уравнение вида log _a f(x)= b равносильно уравнению f(x) = a ^b.

Пример.log ₂ (5 – x) = 3.

5 – х = 2³,

х = — 3.

Ответ. х = — 3.

3) Уравнения вида log _a f (x) = g(x).

Уравнение вида log _a f (x) = g(x) равносильно уравнению f (x) = a ^g(x).

Пример. lg (2^x + x + 4) = x – x lg5.

2^x + x + 4 =10 ^{x — x lg5} ,

2^x + x + 4 = ,

2^x + x + 4 = ,

2^x + x + 4 =,

2^x + x + 4 = 2^x,

x = — 4.

Ответ. х = — 4.

4) Уравнения вида log _a f (x) = log _a g (x).

1способ решения. Уравнение вида log _a f (x) = log _a g (x) равносильно системе: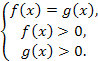

Причем любую из двух последних строк можно (и, как правило, нужно) опустить.

Пример. log₂ (x² + x — 2) = log₂2x.

x = 2.

Ответ. x = 2.

2способ решения. Решив уравнение f(x) =g(x), сделать проверку найденных корней для исходного уравнения.

Пример. log₂(5x + 3)= log₂(7x + 5).

5x + 3 = 7x + 5,

2x = 2, x = — 1.

Проверка. x = -1.

Число x = -1 не является корнем исходного уравнения, так как при x = -1 левая и правая части уравнения теряют смысл.

Ответ. Корней нет.

5) Уравнения вида log _a(x) f(x) = log _a(x) g(x).

Уравнение вида log _a(x) f(x) = log _a(x) g(x)

равносильно системе: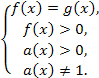или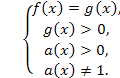

Пример. log _{4 — x} (x² + 1) = log _{4 — x} (3x + 1).

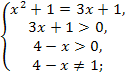
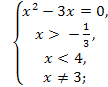
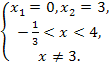x = 0.

Ответ. x₁ = 0.

6) Уравнения вида log _a (log _b f (x)) = c.

При решении уравнений вида log _a (log _b f (x)) = c вначале потенцируют по внешнему логарифму, затем по внутреннему.

Пример. log(log₃x) = 4.

log₂(log₃x) = 2 или log ₂(log₃x) = — 2.

1) log₂(log₃x) = 2; log₃x = 4; x = 81.

2) log₂(log₃x) = — 2; log₃x = ; x = .

Ответ. x₁ = 81, x₂ = .

7) Замена переменной.

Пример. lg² + lg x = 7.

(lg 10 – lg x)² + lg x = 7,

(1 – lg x)² + lg x = 7.

Пусть lg x = у, тогда (1 – у)² + у = 7,

1- 2у + у² + у – 7 = 0,

у² – у – 6 = 0,

у₁ = 3, у₂ = — 2.

Возвращаясь к переменной х, рассмотрим два случая:

1) lg x = 3, x = 10³, x₁ = 1000.

2) lg x = -2, x = 10^-2, x₂ = 0,01.

Ответ. x₁ = 1000, x₂ = 0,01.

8) Приведение к одному основанию.

Пример. = 2 — 2.

= — ,

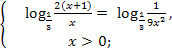
Решим уравнение 18x² + 18x – 1= 0.

х_1,2 = , х_1,2 = , х_1,2 = , х_1,2 = , х_1,2 = ,

Условию удовлетворяет х = .

Ответ. х = .

9) Уравнения с неизвестным в основании логарифма.

Пример 1.log _x 5 = 3.

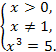x =

Ответ. x =

Пример 2. = 0,5.

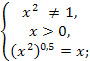
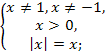
0 < x < 1, x > 1.

Ответ. 0 < x < 1, x > 1.

Пример 3. log_(-x) 25 = — 2.

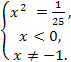x = — .

Ответ. x = — .

Пример 4. + = 2.

ОДЗ уравнения:

+ = 2, + = 2, x² = 48, x_1,2= ± 4.

x = — 4 не удовлетворяет ОДЗ.

Ответ. x = 4.

10) Уравнения вида log _a f (x)∙log _b g(x) = 0.

Уравнения вида log _a f(x)∙ log _b g(x) = 0 равносильно системе:

Пример. log₂x ∙log₇(3 – x) = 0.

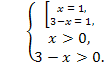
x₁ = 1, x₂ = 2.

Ответ. x₁ = 1, x₂ = 2.

11) Разложение на множители левой части уравнения.

Пример. log₄ (2x – 1)∙log₄x = 2 log₄(2x – 1).

log₄ (2x – 1) ∙ log₄x — 2 log ₄(2x – 1) = 0,

log₄ (2x – 1) ∙ (log ₄ x – 2) = 0,

log₄ (2x – 1) = 0 или log₄ x – 2 = 0.

1) log ₄ ( 2x – 1) = 0, 2x – 1 = 1, x₁ = 1.

2) log ₄ x – 2 = 0, log₄x = 2, x₂ = 16.

Проверка показывает, что оба значения x являются корнями исходного уравнения.

Ответ. x₁ = 1, x₂ = 16.

12) Использование формулы перехода к новому основанию.

Пример.log₃ x + log _x 3 = .

Уравнение имеет смысл при x > , x 1.(1)

Воспользовавшись формулой log _x 3 = , имеем: log₃x + = .

Введем замену log₃x = t, t

t + = , 2t² – 5t + 2 = 0. t₁ = 2, t₂ = .

1) Если t₁ = 2, то log₃x = 2, x₁ = 9.

2) Если t₁ = , то log₃x = , x₂ = .

Найденные значения x удовлетворяют условиям (1) и являются корнями данного уравнения.

Ответ. x₁ = 9, x₂ = .

13) Использование формулы log _a b + log _a c = log _a (bc).

Пример.log ₂ (1 – x)= 3 – log ₂ (3 – x).

log₂ (1 – x)+ log ₂ (3 – x) = 3,

log₂((1 – x) (3 – x)) = 3,

(1 — x)(3 — x) = 8,

x² — 4x — 5 = 0.

x₁ = — 1, x₂ = 5.

Проверка.

x₁ = — 1.

Левая часть уравнения log ₂ (1 – x)= log ₂ (1 — (-1)) = log ₂2 = 1.

Правая часть уравнения 3 — log ₂ (3 – x) = 3 — log ₂ (3 – (-1)) =3 – log ₂ 4 = 3 – 2 = 1.

1 = 1 верно, x₁ = — 1 корень исходного уравнения.

x₂ = 5.

Число x₂ = 5 не является корнем исходного уравнения, так как при x = 5 левая и правая части уравнения теряют смысл.

Ответ. x = — 1.

14) Использование формулы log _a b — log _a c = log _a (b/c)

Пример. lg (x — 1) – lg (2x – 11) = lg 2.

lg = lg 2,

= 2,

x – 1 = 2∙ (2x -11),

3x = 21, x = 7.

Проверка. x = 7.

lg (x — 1) – lg (2x – 11) = lg (7 — 1) – lg (2∙7 – 11) = lg 6 – lg 3 = lg = lg 2.

lg 2 = lg 2 верно, x = 7 корень данного уравнения.

Ответ. x = 7.

15)Уравнения вида A∙( log _a f (x))² + B∙ log _a f (x) + C = 0 .

(f (x) > 0, а > 0,а ≠ 1) путем замены log _a f (x) = t сводится к квадратному уравнению.

Пример. + = 5.

ОДЗ уравнения х > 0.

2 + = 5,

2 + = 5,

2∙ — 2 + — 4∙ + 4 — 5 = 0,

— 2∙ — 3 = 0.

Обозначив = t, получим квадратное уравнение: t² — 2t — 3 = 0, корни которого

t₁ = — 1, t₂ = 3

Возвращаясь к переменной х, рассмотрим два случая:

= -1, х₁ = 3.

2) = 3, х₂ = . Оба значения входят в ОДЗ.

Ответ. х₁ = 3 , х₂ = .

16) Показательно — логарифмические уравнения.

Если в уравнении содержится выражение вида , то для нахождения корней уравнения необходимо сначала прологарифмировать обе его части по тому же основанию, что и основание логарифма, стоящего в показателе степени, а затем решить получаемое алгебраическое уравнение относительно log _a x.

Пример. = 4.

ОДЗ уравнения: x > 0, x ≠ 1.

Прологарифмируем обе части уравнения по основанию 2:

= log ₂ 4, (log ₂ x — 1) ∙ log ₂ x = 2, (log ₂ x)² — log ₂ x — 2 = 0.

Пусть log ₂ x = t , тогда t² — t — 2 = 0, откуда t = 2, t = -1,

Возвращаясь к переменной х, рассмотрим два случая:

1) log ₂ x = 2, x₁ = 4.

2) log ₂ x = — 1, x₂ =. Оба значения удовлетворяют ОДЗ.

Ответ. x₁ = 4, x₂ =.

17) Использование однородности.

Уравнения вида a∙A²(х)+ b∙A(х)B(х) + c∙B²(х) = 0 называются однородными

Способ решения однородных уравнений:

деление обеих частей уравнения на A²(х), A(х)B(х) или B²(х) и введение замены.

Пример. lg²(x + 1) = lg(x + 1) lg(x — 1) + 2 lg²(x — 1).

ОДЗ x > 1,

lg²(x + 1) — lg(x + 1) lg(x — 1) — 2 lg²(x — 1) = 0,

Разделим на lg²(x — 1) 0.

— — 2 = 0,— — 2 = 0.

Пусть у = , тогда у² – у – 2 = 0, откуда у₁ = 2, у₂ = -1.

Возвращаясь к переменной х, рассмотрим два случая:

1) = 2, lg(x + 1) = 2 lg(x — 1), lg(x + 1) = lg(x — 1)², х + 1 = (х – 1)²,

х + 1 = x² — 2х + 1 , x² — 3х = 0, (x – 3)х = 0. x₁ = 3, x₂ = 0.

x₂ = 0 не удовлетворяет ОДЗ.

2) = -1, lg(x + 1) = — lg(x — 1), lg(x + 1) = lg, x + 1 = , x² – 1= 1, x²= 2.

x_1,2 =

x₂ = не удовлетворяет ОДЗ.

Ответ. x₁ = 3, x₂ = .

18) Уравнения вида = g(x).

Уравнение вида = g(x) равносил