|
|
|
МОУ «Лицей №1» (физико-математический) |
|
Мастер-класс
Контактный телефон 422387 Лицей №1 (физико-математический) г.Норильск ул.Севастопольская,8а |
ЛИЦЕЙ №1
|
МАСТЕР-КЛАСС ТЕМА: Система подготовки учащихся к ЕГЭ (10-11 класс). Обучающие и контролирующие тесты по математике. Учитель математики Сергеева Светлана Михайловна |
|
|
| Норильск 2005/2006 уч.г. |
Уравнения и неравенства. Системы уравнений.
Решение любого вида уравнений и неравенств сопряжено с проведением тождественных преобразований различных выражений, входящих в заданное уравнение (неравенство), а также с проведением равносильных преобразований. Владение формулами для тождественных преобразований выражений и теоремами о равносильных преобразованиях уравнений и неравенств помогут вам в поиске рационального решения заданий теста.
Задания А4, А8 и А9 приводят к решению уравнений, в заданиях А5 и А7 предлагаются иррациональные уравнение и неравенство.
В первой части есть три задания с параметром на зависимость количества корней квадратного уравнения от его дискриминанта (А2 и А3) и определение квадратного уравнения.
Задания А8-А10 приводят к решению уравнений и системы уравнений в результате применения характеристических свойств арифметической и геометрической прогрессий, способствуют повторению формул и свойств прогрессий.
Задачи части В более сложные, рассчитаны на учащихся, имеющих прочные базовые знания.
В заданиях В2-В4 предлагаются неравенство, уравнение и система уравнений, решаемые методом введения новой переменной.
Остальные задания второй части содержат параметр.
В задании В1 используется условие равенства дроби нулю, в задании В7 при ответе на вопрос об отсутствии корней уравнения надо различить два случая: когда уравнение является линейным и когда квадратным.
В задании В5 при решении биквадратного уравнения рассмотреть не только случай отрицательного дискриминанта, но и наличие отрицательных корней квадратного уравнения, полученного в результате замены переменной. ЖЕЛАЕМ УСПЕХА!
§ 2. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
СИСТЕМЫ УРАВНЕНИЙ.
Вариант №1.
Часть 1
А1. Найти сумму целых чисел, являющихся решениями неравенства
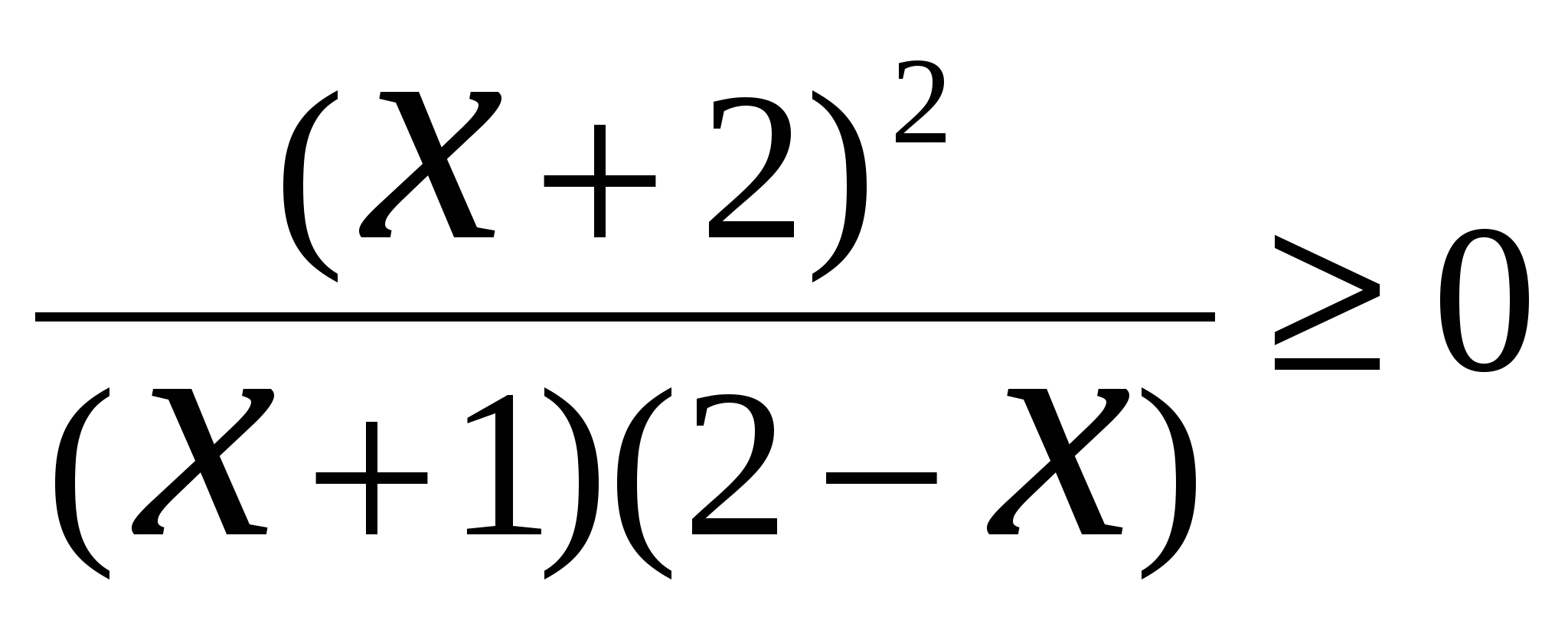 .
.
(1) –1; (2) 2; (3) 1; (4) 0; (5) 3; (6) –2.
А2. При каких значениях параметра ![]() уравнение 5х2 – 4х +
уравнение 5х2 – 4х + ![]() = 0 не имеет действительных корней?
= 0 не имеет действительных корней?
(1) ![]() =
= ![]() ; (2) 0 <
; (2) 0 <![]() <
< ![]() ; (3) 0 <
; (3) 0 < ![]() <1;
<1;
(4) ![]() >
> ![]() ; (5)
; (5) ![]() > 1; (6)
> 1; (6) ![]() < 0.
< 0.
А3. При каких значениях параметра а график функции f(x) = аx2 + 2x + 1
имеет единственную общую точку с осью Ох?
(1) а = 1; (2) а < 1, а ≠ 0; (3) а1 =![]() , а2 = 0;
, а2 = 0;
(4) а = ± 1; (5) а1 = 0, а2 = 1; (6) а ![]() (0, 1).
(0, 1).
А4. Найти сумму корней уравнения
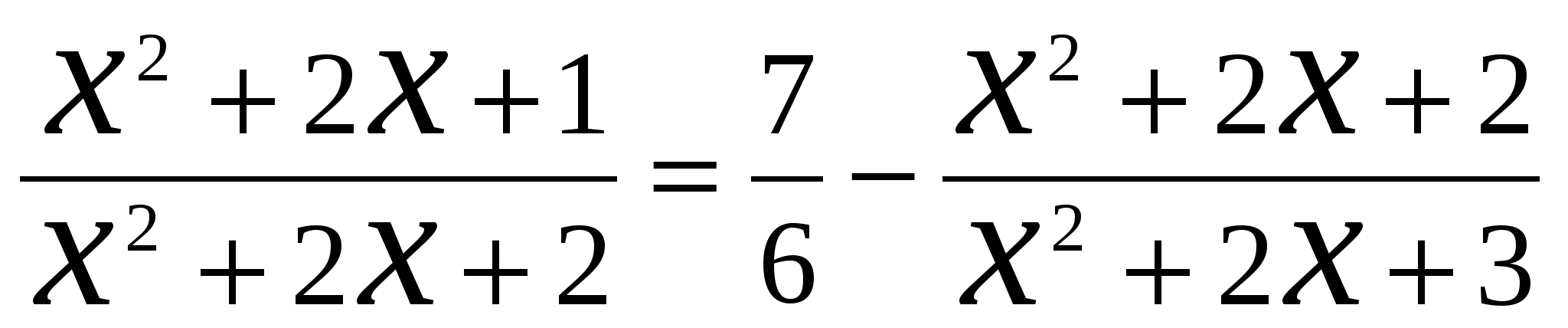 .
.
(1) ![]() ; (2)
; (2) ![]() ; (3)
; (3) ![]() ; (4) 2.
; (4) 2.
А5. При каких значениях параметра ![]() число 2 является корнем уравнения
число 2 является корнем уравнения
![]() ?
?
(1) ![]() 1 =
1 = ![]() ,
, ![]() 2 = 1; (2)
2 = 1; (2) ![]() =
=![]() ; (3)
; (3) ![]() = 1; (4)
= 1; (4) ![]()
![]() 1.
1.
А6. Найти все целые значения ![]() , для которых выполняется неравество
, для которых выполняется неравество
f(![]() )
) ![]() f(
f(![]() + 2), если f(
+ 2), если f(![]() ) =
) = 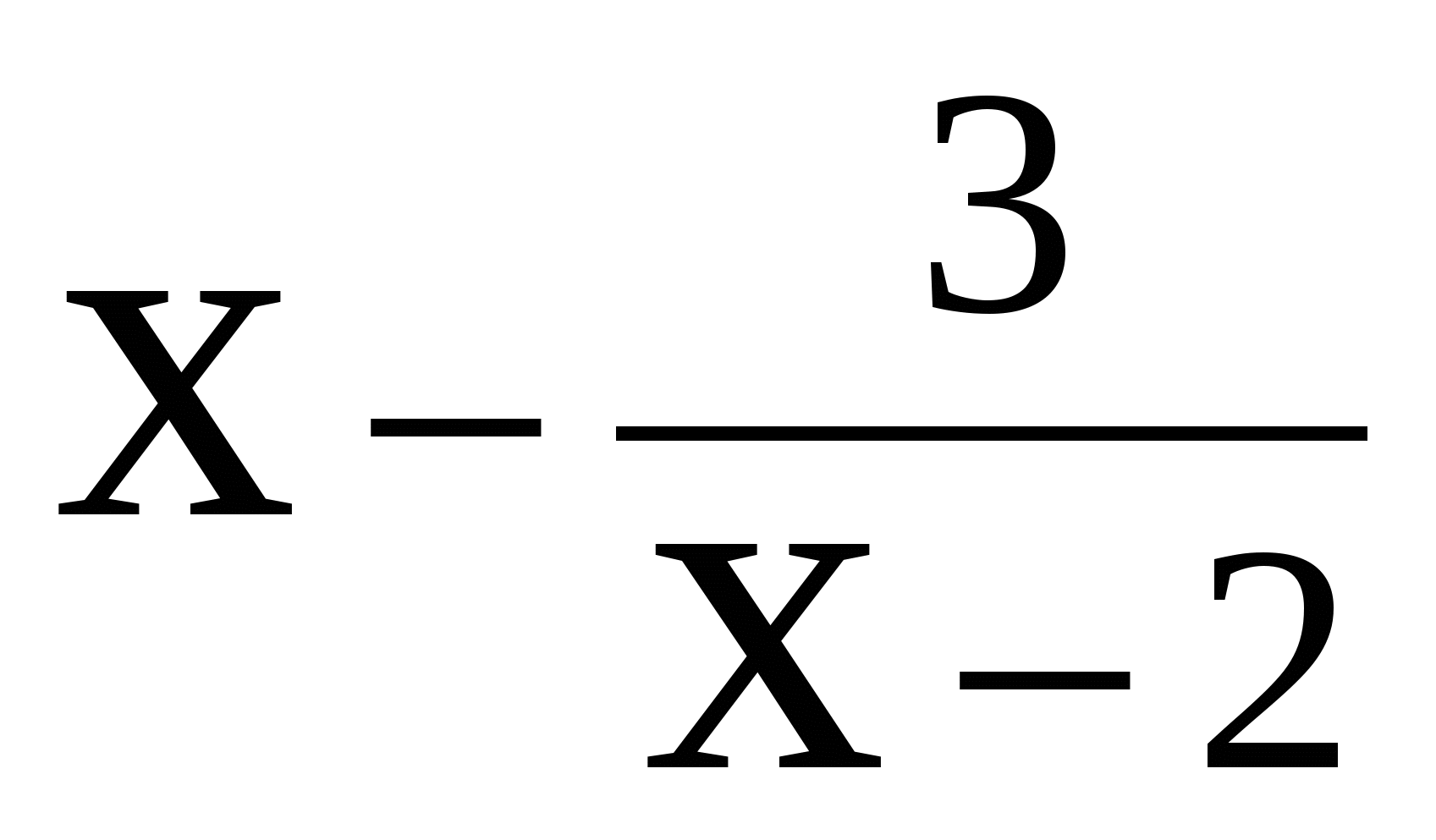 .
.
(1) ![]() 1 = 0,
1 = 0, ![]() 2 = 1; (2)
2 = 1; (2) ![]() 1 = 1,
1 = 1, ![]() 2 = 2; (3)
2 = 2; (3) ![]() = 1;
= 1;
(4) ![]() 1 = 0,
1 = 0, ![]() 2 = 1; (5)
2 = 1; (5) ![]() 1 = 2,
1 = 2, ![]() 2 = 3; (6)
2 = 3; (6) ![]() = 0.
= 0.
А7. Решить неравенство ![]() .
.
(1) 2 ≤ ![]() ≤ 14; (2) —2 <
≤ 14; (2) —2 < ![]() ≤ 2;
≤ 2;
(3) —2 < ![]() < 5; (4) —2 <
< 5; (4) —2 < ![]() ≤ 14.
≤ 14.
А8. При каких значениях ![]() числа 3
числа 3![]() ,
, 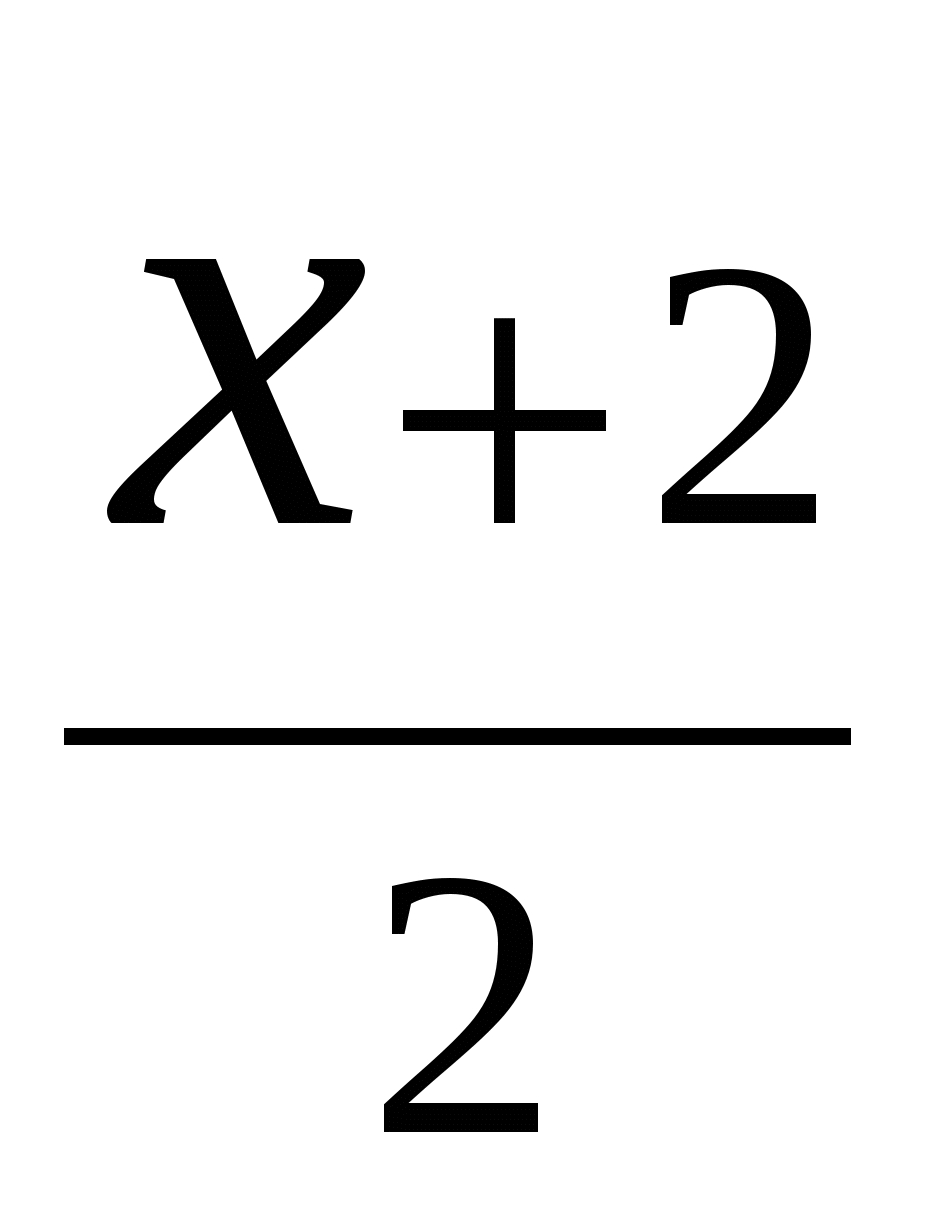 и
и ![]() являются тремя последовательными членами арифметической прогрессии?
являются тремя последовательными членами арифметической прогрессии?
(1) ![]() =
= ![]() ; (2)
; (2) ![]() =
= ![]() ; (3)
; (3) ![]() = 1; (4)
= 1; (4) ![]() =
= ![]() .
.
А9. При каких значениях ![]() числа 2
числа 2![]() ,
, ![]() и
и ![]() являются тремя последовательными членами геометрической прогрессии?
являются тремя последовательными членами геометрической прогрессии?
(1) ![]() 1 = –16,
1 = –16, ![]() 2 = 4; (2)
2 = 4; (2) ![]() 1 = –12,
1 = –12, ![]() 2 = 8;
2 = 8;
(3) ![]() 1 = –8,
1 = –8, ![]() 2 = –4; (4)
2 = –4; (4) ![]() = –16.
= –16.
А10. Сумма первых шести членов арифметической прогрессии равна 9, а разность между четвертым и вторым членами равна 0,4. Найти первый член этой прогрессии.
(1) 2; (2) 0,5; (3) –1; (4) 3; (5) 6; (6) 1.
Часть 2.
В1. При каких значениях параметра ![]() уравнение
уравнение
![]()
имеет единственное решение?
В2. Решить неравенство ![]() .
.
В3. Решить уравнение ![]() .
.
В4. Найти произведение всех значений ![]() и
и ![]() , являющихся решениями системы
, являющихся решениями системы
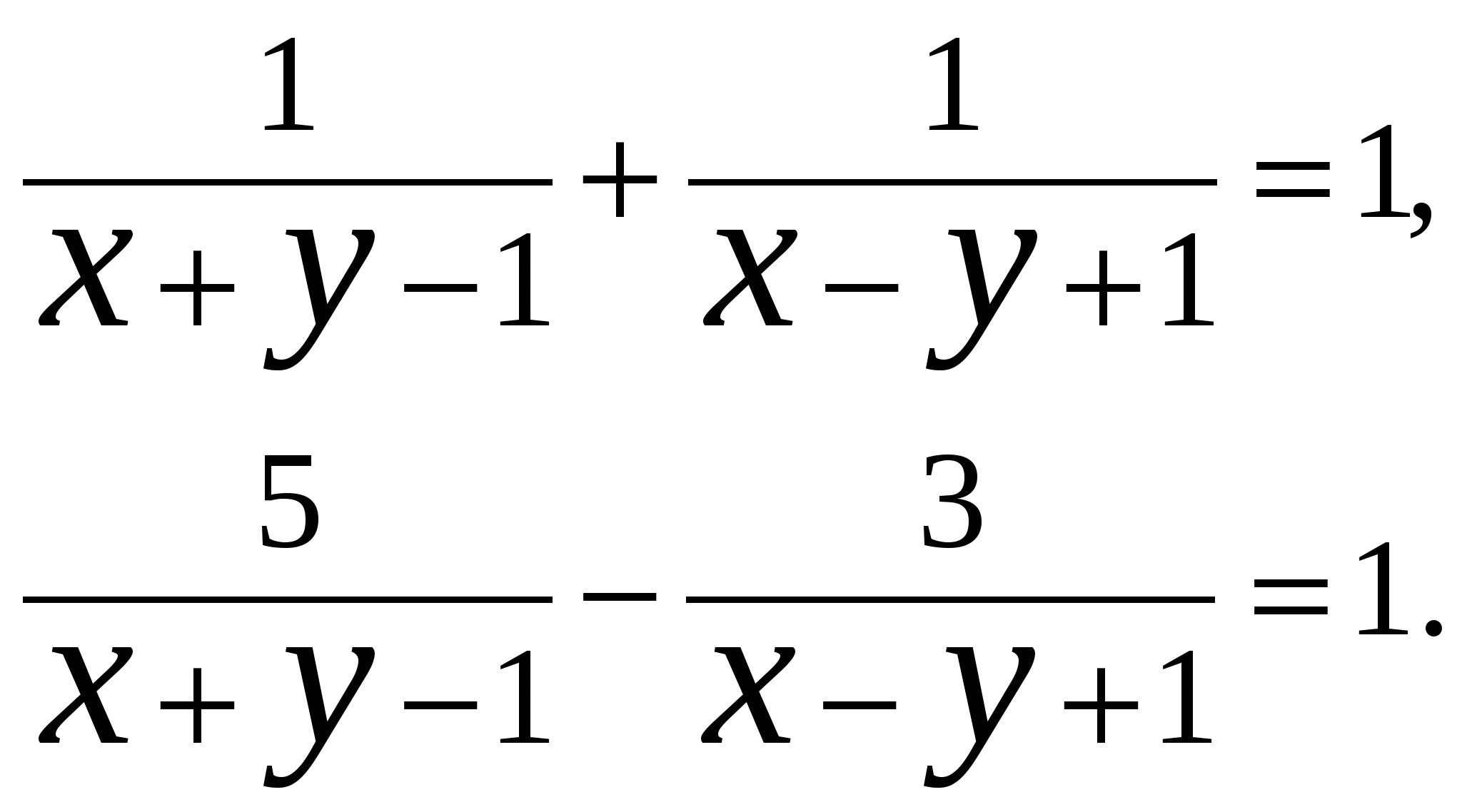
В5. Найти все значения параметра ![]() , при которых уравнение
, при которых уравнение
![]() не имеет корней.
не имеет корней.
В6. При каких значениях параметра ![]() система
система 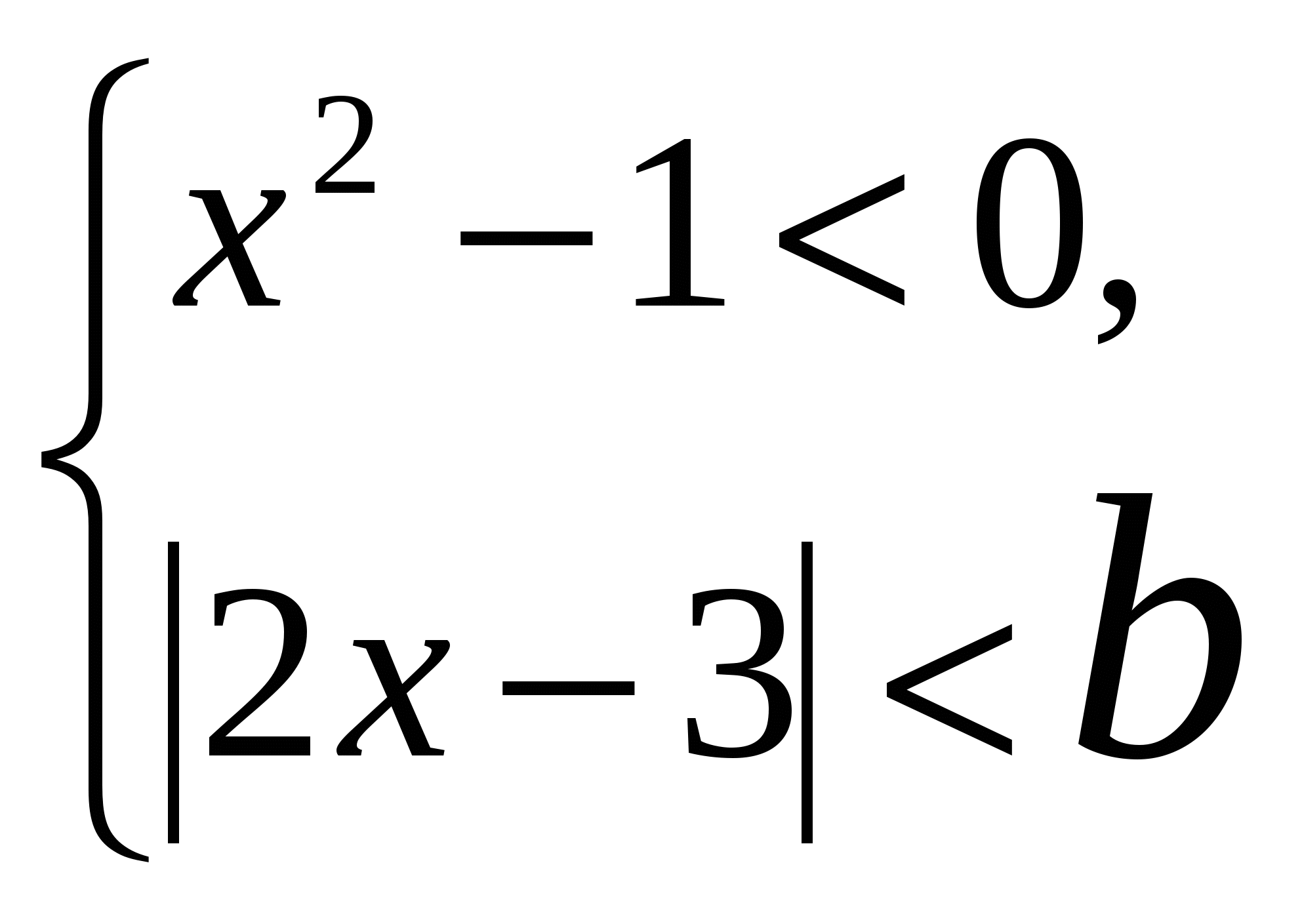 не имеет решения?
не имеет решения?
В7. При каких значениях параметра ![]() графики функций
графики функций ![]() и
и ![]()
не пересекаются ?
Номера верных ответов части 1 теста по теме «АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА. Системы уравнений».
| А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | А9 | А10 | |
| Вариант 1 | 1 | 4 | 5 | 3 | 3 | 3 | 4 | 1 | 1 | 6 |
Ответы к заданиям части 2.
| В1 | В2 | В3 | В4 | В5 | В6 | В7 | |
| Вариант 1 |
| 0 ≤ х < 1, х > 4. |
| 2 |
|
|
|
ТРИГОНОМЕТРИЯ
СТАРТОВЫЙ ТЕСТ
Цель тестирования – установить степень готовности учащихся 10 классов к решению различных видов тригонометрических уравнений, неравенств, систем уравнения
Задачи тестирования:
1. Оценка уровня усвоения учащимся ключевых понятий курса тригонометрии, необходимых в качестве опорных знаний при решении тригонометрических уравнений, неравенств, систем уравнения.
2. Выявления пробелов в знании учащихся с целью организации коррекционной работы.
Стартовый тест по алгебре и началам анализа для учащихся 10 классов составлен с учетом требований к обязательному уровню усвоения содержания обучения. Тест представлен в 2-х эквивалентных вариантах по 8 заданий в каждом и рассчитан на 15 минут. Все задания данного теста — с закрытой формой ответов.
Основная цель учителя – обеспечить самостоятельную работу каждого учащегося.
Стартовый тест по алгебре и началам анализа в 10 классе.
Тригонометрические уравнения.
I вариант.
Указание. Тест состоит из 8 заданий и рассчитан на 15 минут. Эти задания имеют предлагаемые ответы, обозначенные буквами а, б, в, г. Выберете среди предложенных ответов правильный (единственный) и зачеркните на бланке ответов соответствующую ему букву.
1. Вычислите без таблиц и калькуляторов ![]() .
.
![]() ;
; ![]() ;
; 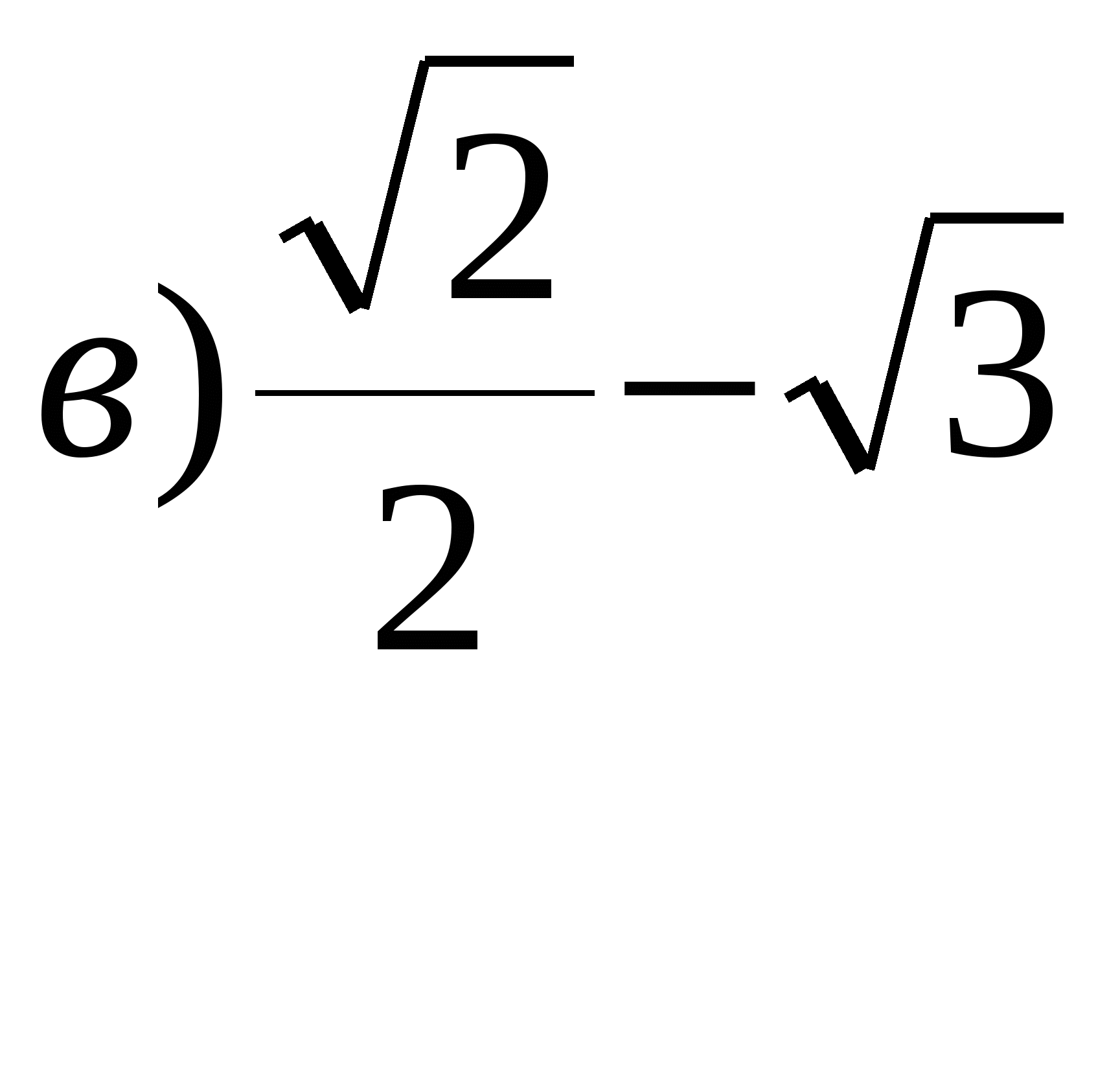 ;
; ![]() ;
;
2. Вычислить ![]() .
.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
3. Вычислите ![]() .
.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
4. Вычислите arctg 1 + arccos 0 + arcsin![]() + arcctg
+ arcctg![]()
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
5. Вычислите 3arccos ![]() + 2arcsin(-1) —
+ 2arcsin(-1) — ![]() arctg
arctg![]() .
.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
6. Записать формулу корней уравнения tgx = a.
а) ![]() arctga +
arctga + ![]() k, k
k, k![]() z; б) arctga + 2
z; б) arctga + 2![]() k, k
k, k![]() z;
z;
в) ![]() arctga + 2
arctga + 2![]() k; k
k; k![]() z; г) arctga +
z; г) arctga + ![]() k; k
k; k![]() z;
z;
7. Сколько корней имеет уравнение sin3x = ![]() ?
?
а) один; б) два;
в) бесконечное множество; в) ни одного.
8). Сколько корней имеет уравнение ctg2x = 1?
а) один; б) два;
в) бесконечное множество; в) ни одного.
Стартовый тест по алгебре и началам анализа в 10 классе.
Тригонометрические уравнения.
II вариант.
Указание. Тест состоит из 8 заданий и рассчитан на 15 минут. Эти задания имеют предлагаемые ответы, обозначенные буквами а, б, в, г. Выберете среди предложенных ответов правильный (единственный) и зачеркните на бланке ответов соответствующую ему букву.
1. Вычислите без таблиц и калькуляторов ![]() .
.
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
2. Вычислить ![]() .
.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
3. Вычислите ![]() .
.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
4. Вычислите arcsin 0 + arctg![]() + arccos
+ arccos![]() + arcctg
+ arcctg![]()
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
5. Вычислите 3arcsin![]() + 2arccos(-1) —
+ 2arccos(-1) — ![]() arcctg1.
arcctg1.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
6. Записать формулу корней уравнения cosx = a.
а) arccos a+ 2![]() k, k
k, k![]() z; б)
z; б) ![]() arcos a + 2
arcos a + 2![]() k, k
k, k![]() z;
z;
в) ![]() arccos a +
arccos a + ![]() k; k
k; k![]() z; г) arccos a +
z; г) arccos a + ![]() k; k
k; k![]() z;
z;
7. Сколько корней имеет уравнение sinx = 2?
а) один; б) два;
в) бесконечное множество; в) ни одного.
8). Сколько корней имеет уравнение tg3x = ![]() ?
?
а) один; б) два;
в) бесконечное множество; в) ни одного.
Ответы к стартовому тесту:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Вариант 1 | б | а | в | а | б | г | г | в |
| Вариант 2 | б | а | а | г | б | а | г | в |
Тренинговый тест.
Тест предназначен для тренинга учащихся 10 классов по решению тригонометрических уравнений, систем уравнений.
Цель тестирования:
1. Знакомство учащихся с особенностями процедуры тестирования.
2. Диагностика уровня обученности учащихся.
Задача тестирования:
1. Подготовка учащихся к тематическому тестированию.
2. Проверка уровня усвоения общеучебных умений и навыков.
Требованиями обязательного уровня обученности, заложенной в данном тексте, определенны содержанием учебной программы по математике. Объем и уровень сложности задания соответствует возрастным особенностям ученика.
Тест позволяет оценить уровень сформированности навыков решения различных видов тригонометрических уравнений, систем уравнений. Он представлен в 4-х эквивалентных вариантах по 10 заданий в каждом и рассчитан на 2 часа.
Тест по алгебре и началам анализа
(Тренинг) 10 класс
Тригонометрические уравнения, системы уравнения.
I Вариант
Инструкция. Тест состоит из 10 заданий и рассчитан 2 часа. Выполняйте задания в предложенной последовательности, внимательно прочитав указания к каждой части. Не задерживайтесь слишком долго на одном задании. Если не можете выполнить очередное задание, переходите к следующему. Приступайте к выполнению теста. Желаем успеха!!
Часть I (Задания 1 — 5)
Указание. Эти задания имеют предполагаемые ответы, обозначенные буквами а, б, в, г. Выберите среди предложенных ответов правильный (единственный) и зачеркните на бланке ответов соответствующую ему букву.
1. Сколько корней имеет уравнение sinx = —![]()
а) один б) два
в) бесконечное множество г) ни одного
2. Решите уравнение ctgx = 0
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
3. Решите уравнение 3tg![]()
а) ![]() б)
б) ![]()
в) ![]() г) не имеет решения;
г) не имеет решения;
4. При каком значении х выражение sin![]() равняется 1?
равняется 1?
а) ![]() б)
б) ![]()
в) ![]() г) не существует такого значения х.
г) не существует такого значения х.
5. Решите уравнение ![]()
а) ![]() б)
б) ![]()
в) ![]() г)
г) ![]()
Часть II (задания 6 — 10).
Указания. Эти задания выполняются на отведенных для ответов местах.
6. Решите уравнение ![]()




7. Решите уравнение ![]()




8. Решите уравнение ![]()




9. Решите систему уравнений 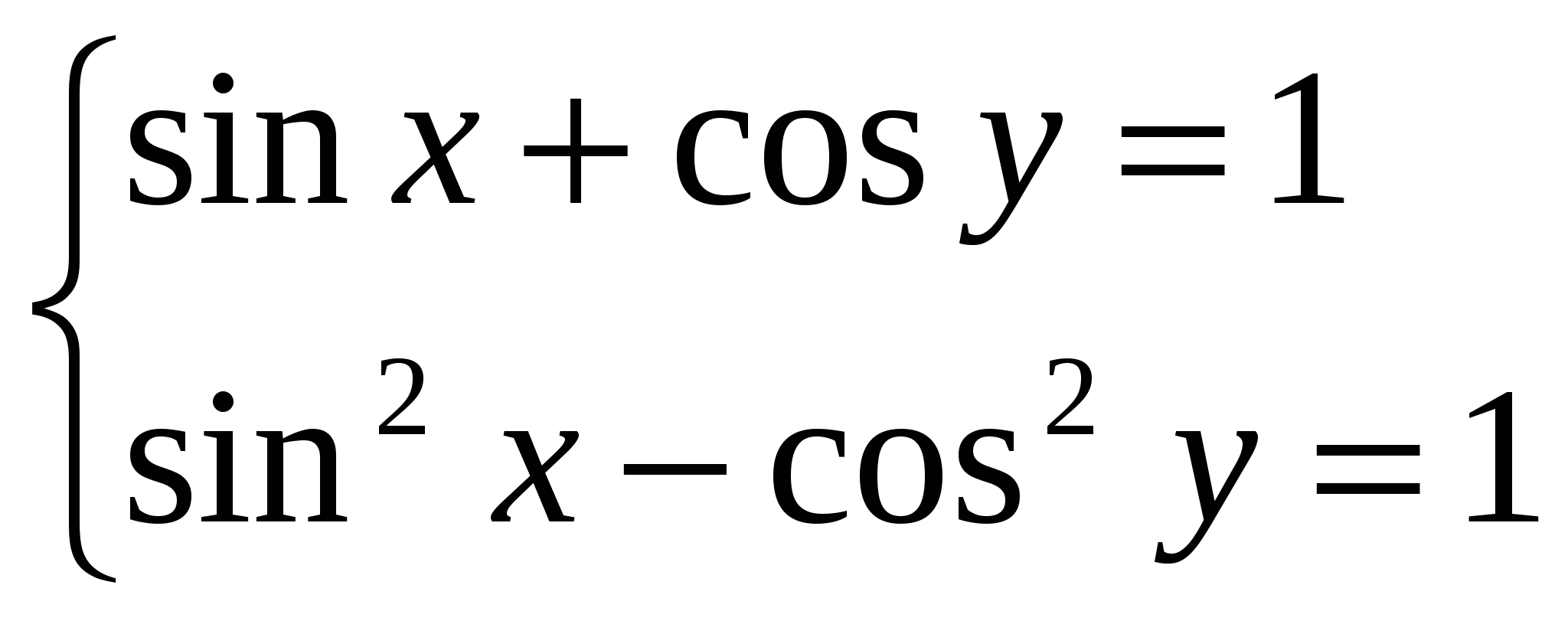




10. Решите систему уравнений 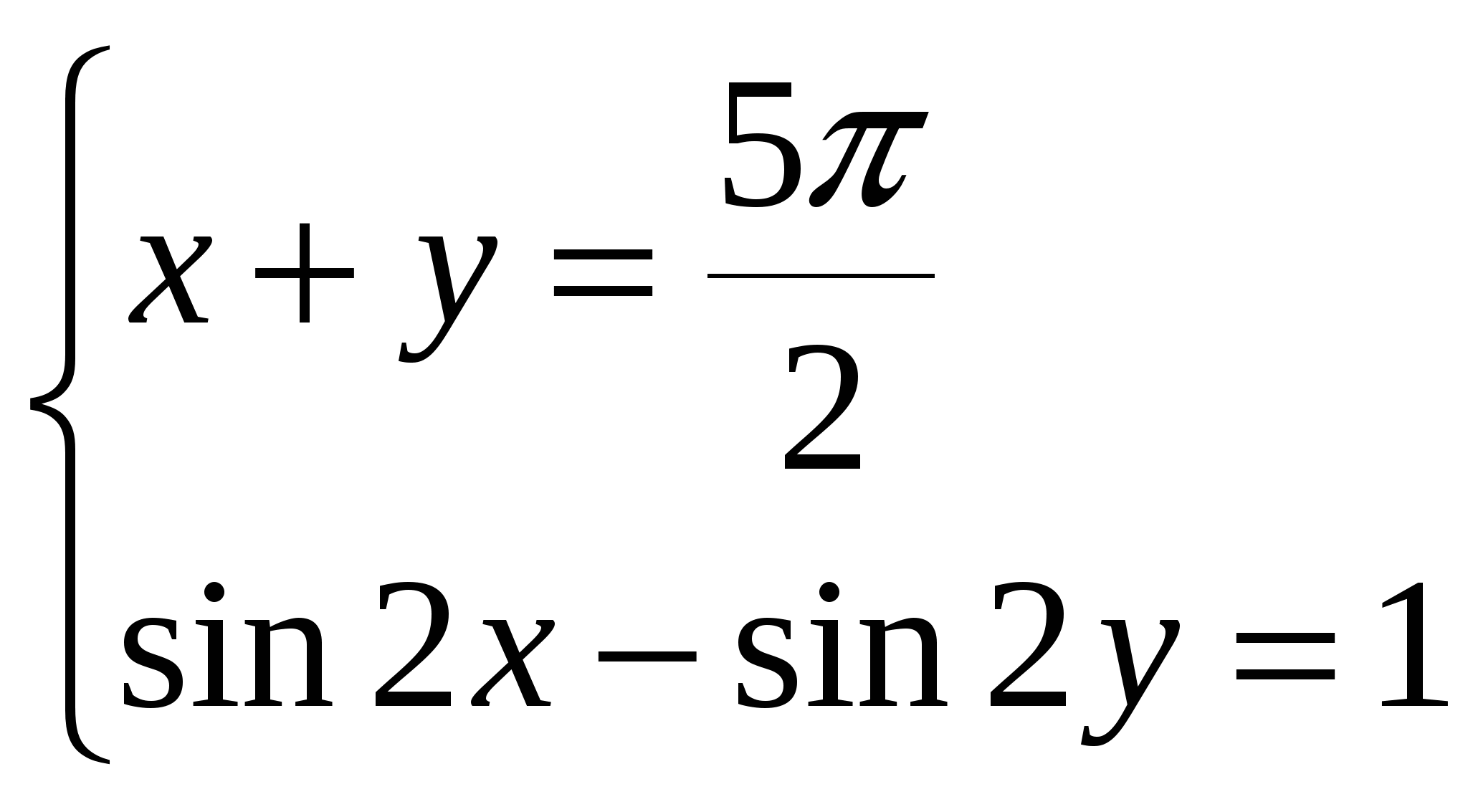
Тест по алгебре и началам анализа
(Тренинг) 10 класс
Тригонометрические уравнения, системы уравнения.
II Вариант
Инструкция. Тест состоит из 10 заданий и рассчитан 2 часа. Выполняйте задания в предложенной последовательности, внимательно прочитав указания к каждой части. Не задерживайтесь слишком долго на одном задании. Если не можете выполнить очередное задание, переходите к следующему. Приступайте к выполнению теста. Желаем успеха!!
Часть I (Задания 1 — 5)
Указание. Эти задания имеют предполагаемые ответы, обозначенные буквами а, б, в, г. Выберите среди предложенных ответов правильный (единственный) и зачеркните на бланке ответов соответствующую ему букву.
1. Сколько корней имеет уравнение sinx = -2
а) один б) два
в) бесконечное множество г) ни одного
2. Решите уравнение ctgx = 0
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
3. Решите уравнение ![]()
а) ![]() б)
б) ![]()
в) ![]() г) не имеет решения;
г) не имеет решения;
4. При каком значении х выражение sin![]() равняется 1?
равняется 1?
а) ![]() б)
б) ![]()
в) ![]() г) не существует такого значения х.
г) не существует такого значения х.
5. Решите уравнение ![]()
а) ![]() б)
б) ![]()
в) ![]() г) не имеет решения.
г) не имеет решения. ![]()
Часть II (задания 6 — 10).
Указания. Эти задания выполняются на отведенных для ответов местах.
6. Решите уравнение ![]()




7. Решите уравнение ![]()




8. Решите уравнение ![]()




9. Решите систему уравнений 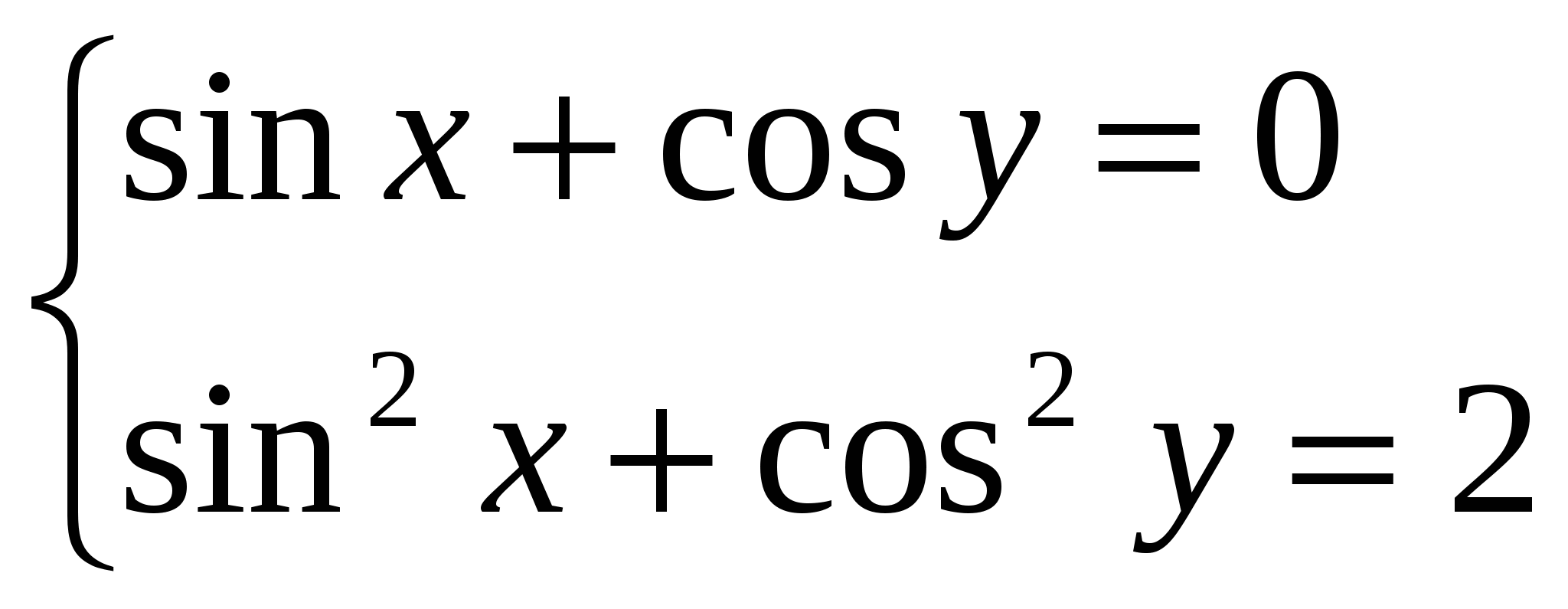




10. Решите систему уравнений 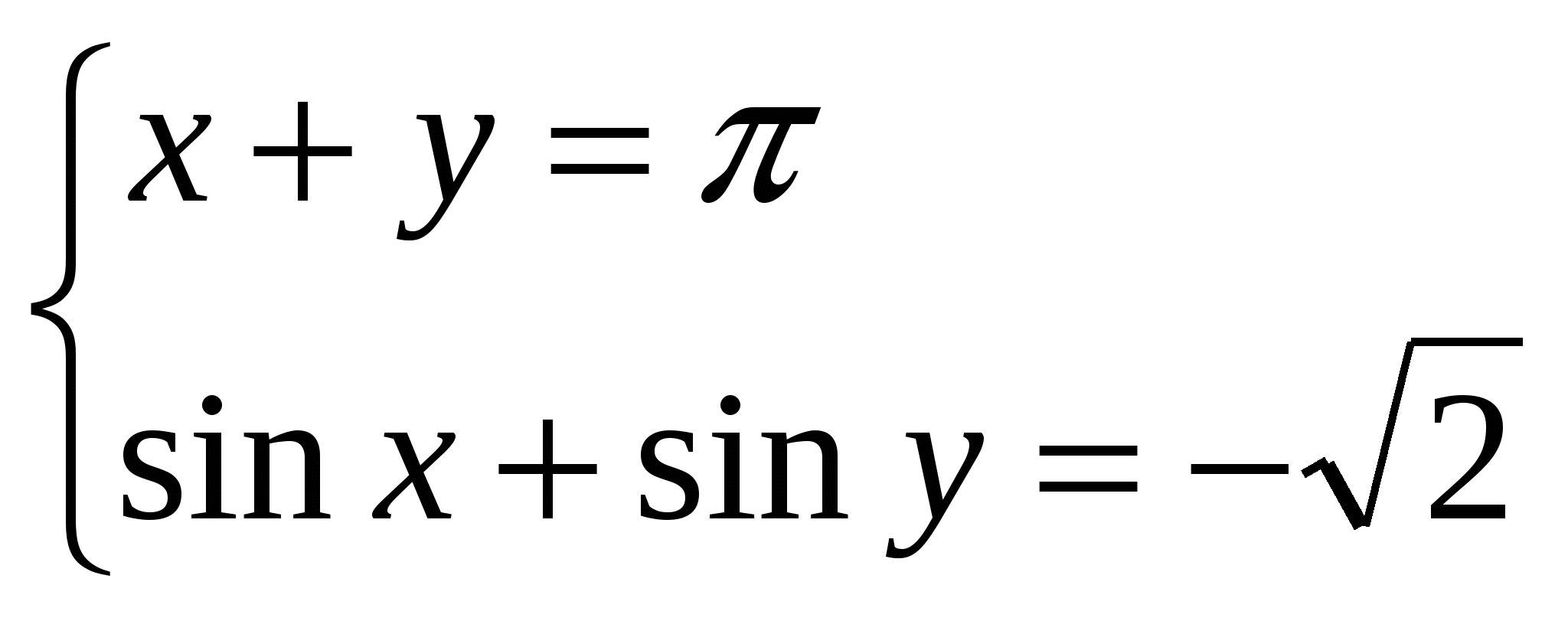
Тематический тест по алгебре и началам анализа
10 класс
Тригонометрические уравнения, неравенства, системы уравнения.
I Вариант
Инструкция. Тест состоит из 9 заданий и рассчита
