Муниципальное бюджетное общеобразовательное учреждение
гимназия № 19 им.Н.З.Поповичевой г.Липецка
Конспект урока по алгебре
в 7 классе
Формулы сокращённого умножения.
Квадрат суммы и разности двух выражений
подготовила
учитель математики
Маликова Ольга Георгиевна
Липецк, 2013
Тема урока: Формулы сокращённого умножения. Квадрат суммы и
разности двух выражений
Тип урока: «открытие» нового знания.
Цели урока:
1) Дидактические: выведение формул квадрата суммы и квадрата разности двух
выражений; отработка навыка применения данных формул;
2) Развивающие: развитие логического мышления и мировоззрения
учащихся.
3) Воспитательные: воспитание у школьников устойчивого интереса к
математике.
На уроке используются: готовые чертежи, наглядный материал.
Ход урока: 1. Организационный момент
2. Актуализация знаний.
3. Изучение нового.
4. Историческая справка.
5. Закрепление изученного материала.
6. Итог урока.
Ход урока
1. Организационный момент
Ребята, французский писатель XIX столетия Анатоль Франс однажды заметил:
«Учиться можно только с интересом. Чтобы переварить знания, надо поглощать их с
аппетитом!»
Так давайте сегодня на уроке будем следовать этому совету писателя: будем активны, внимательны, будем поглощать знания с большим желанием, ведь они пригодятся вам в дальнейшем.
Сегодня на уроке вам предстоит сыграть роль исследователей, «открыть» две формулы и научиться их применять.
2. Актуализация знаний
А прежде чем перевоплотиться в сотрудников исследовательского института потренируем свой мозг устными упражнениями:
1) Прочитайте выражения:
а) х2+(3у)2; б) (х+3у)2; в) х2 – (3у)2; г) (х – 3у)2; д) 2(х∙3у); е)(х-3у)(х+3у).
— Какие из данных выражений тождественно равны? (в и е)
— Как называется применимая здесь формула? Сформулируйте её. (Разность квадратов двух выражений равна произведению разности этих выражений на их сумму)
2) Возведите в квадрат: а) 6х (36х2);
б) 0,4х2у3 (0,16х4у6);
в) ![]() х3у (
х3у (![]() х6у2).
х6у2).
— Найдите произведение 6х и 0,4х2у3 ; найдите удвоенное произведение этих выражений.
(2,4х3у3; 4,8х3у3)
— Найдите произведение 6х и ![]() х3у; найдите удвоенное произведение этих выражений.
х3у; найдите удвоенное произведение этих выражений.
(3х4у; 6х4у)
3) Решите уравнение: а) х2 – 49 = 0; {7; -7} б) 0,64m – m3 = 0; {0; 0,8; -0,8}
в) 81х2 + 4 = 0. (нет решений)
4) Вычислите: а) (30 – 3)(30 + 3); (891) в) 208 ∙ 192; (39936)
б) 1382 – 1372; (275) г) ![]() .
. ![]()
5) Сравните: а) 123186 ∙ 123188 и 1231872; (123186 ∙ 123188 < 1231872)
б) 792 + 852 и (79 + 85)2; (?)
в) 502 + 392 и (50 – 39)2. (502 + 392 > (50 – 39)2)
— В чём возникло затруднение? (сложные вычисления в задании под буквой «б»)
— Прочитайте выражение слева. (сумма квадратов чисел 79 и 85) Существует ли формула
для суммы квадратов? (нет)
— Прочитайте выражения справа. (квадрат суммы чисел 79 и 85) Знаем ли мы эти
формулы? А хотим узнать?
— Так какие же формулы мы сегодня должны «открыть»?
— Итак, сформулируйте тему нашего сегодняшнего урока.
Откройте тетради, запишите число, классная работа и тему урока.
3. Изучение нового
Теперь мы готовы приступить к исследованию и выполнить основную цель нашего урока: вывести формулы для квадрата суммы и квадрата разности двух выражений.
Вспомним умножение многочленов ( 3 человека работают индивидуально у доски, остальные в тетрадях по вариантам (3 варианта)).
I вариант II вариант III вариант
(х+у)(х+у) = х2+2ху+у2 (m+n)(m+n) = m2+2mn+n2 (c – d)(с – d) = с2-2сd+d2
(7+с)(7+с) = 49+14с+с2 (n+6)(n+6) = n2+12n+36 (9 – а)(9 – а) = 81-18а+а2
Обратите внимание на задания I и II варианта.
— Что общего в задании? (в левой части произведение одинаковых множителей)
— Как произведение одинаковых множителей записать в виде степени? (квадрат суммы)
— Что общего в полученных ответах? (получили сумму квадратов и удвоенное
произведение этих выражений)
— Запишите соответствующую формулу? ((а + b)2 = а2 + 2аb + b2)
— Сформулируйте полученное правило возведения суммы двух выражений в квадрат.
(квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное
произведение первого и второго выражений и плюс квадрат второго выражения)
Обратимся к заданию III варианта.
— Запишите левую часть в виде степени?
— В чём различия результатов, если возводим в квадрат не сумму, а разность двух
выражений? (минус удвоенное произведение)
— Запишите соответствующую формулу. ((а — b)2 = а2 — 2аb + b2)
— Сформулируйте полученное правило возведения разности двух выражений в квадрат.
(квадрат разности двух выражений равен квадрату первого выражения минус
удвоенное произведение первого и второго выражений и плюс квадрат второго
выражения)
4. Немного истории
Некоторые правила сокращённого умножения были известны ещё около 4 тыс. лет
тому назад. Их знали вавилоняне и другие народы древности. Тогда они формулировались словесно или геометрически.
У древних греков величины обозначались не числами или буквами, а отрезками прямых. Они говорили не «а2», а «квадрат на отрезке а», не «а∙b», а «прямоугольник, содержащийся между отрезками а и b». Например, тождество (а + b)2 = а2 + 2аb + b2 во
второй книге «Начал» Евклида (3 в до н.э.) формулировалось так: «Если прямая линия (имеется в виду отрезок), как-либо рассечена, то квадрат на всей прямой равен квадратам на отрезках вместе с дважды взятым прямоугольников, заключённым между отрезками».
Доказательство опиралось на геометрическое соображение.
Некоторые термины подобного геометрического изложения алгебры сохранились
до сих пор. Так, мы называем вторую степень числа – квадратом, а третью степень – кубом числа.
А теперь давайте и мы с помощью рисунка объясним геометрический смысл формулы (а + b)2 = а2 + 2аb + b2. 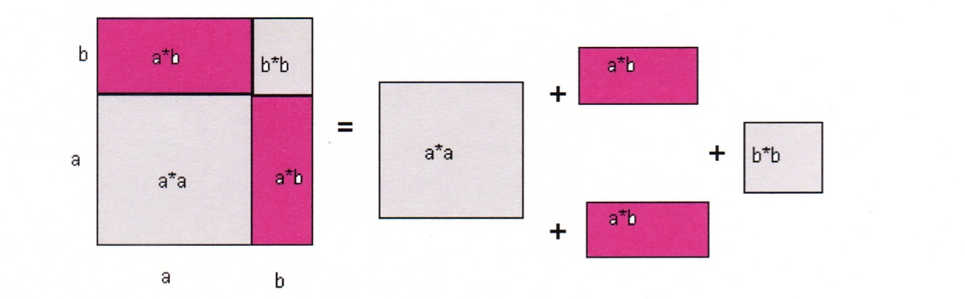
5. Закрепление изученного материала
№ 1 (устно) Выбрать правильный ответ из предложенных.
(с + 11)2 (7у + 6)2 (2х – 3у)2
А с2 + 11с + 121 А 49у2 + 42у + 36 А 4х2 – 12ху + 9у2
В с2 – 22с + 121 В 49у2 + 84у + 36 В 4х2 – 12ху – 9у2
С с2 + 22с + 121 С 49у2 + 36 С 4х2 – 6ху + 9у2
Ответы: С, В, А.
№ 2 (устно) Из актуализации знаний в первом задании найдите квадрат суммы или квадрат разности и представьте в виде многочлена. ((х+3у)2 = х2 + 6ху + 9у2; (х – 3у)2 =
х2 – 6ху + 9у2)
№ 3 (устно) Вернуться к возникшей проблеме в пятом задании и сравнить выражения. ( б) 792 + 852 < (79 + 85)2; в) 502 + 392 > (50 – 39)2.)
№ 690 (а, д) (1 ученик работает на доске остальные самостоятельно в тетрадях, затем ответы комментируют)
№ 690 (б, е) (самостоятельно, 2 человека работают на скрытых досках, затем ответы проверяются)
№ 707 (а) на доске и в тетрадях решить двумя способами: используя формулу квадрат разности и разность квадратов.
6. Итог урока
— Что нового вы сегодня узнали на уроке?
— Чему равен квадрат суммы двух выражений?
— Чему равен квадрат разности двух выражений?
— Чем отличаются формулы?
— Чью работу вы можете сегодня отметить? (Оценки)
Домашнее задание: п. 25, № 682(б), 686(а, г, е, ж), 689, 838*(для желающих)
Благодарю всех сотрудников исследовательского института за проделанную работу. И желаю вам в будущем сделать ещё немало различных открытий.
Используемая литература
1. Макарычев Ю.Н., Миндюк Н.Г. и др. Алгебра. 7 класс: учебник для школ и классов с
углубленным изучением математики. – Москва: Мнемозина, 2008.
2. Юшкевич Ю.П. и др. История математики с древних времён до начала XIX столетия. –
Москва: Наука, 1970.
