Урок алгебры в 7 классе по теме «Системы двух линейных уравнений с двумя переменными»

Урок алгебры в 7 классе по теме

«Системы двух линейных уравнений с двумя переменными»

Урок подготовила и провела:

учитель математики

Тарада Елена Борисовна

Тип урока: обобщающий урок.

Цели урока:

• обобщение и систематизация знаний учащихся по теме “ Системы двух линейных уравнений с двумя переменными», закрепление умений решения систем уравнений различными способами, а именно: способом подстановки, способом сложения (вычитания), графическим способом;

• развитие познавательного интереса.

Задачи урока:

• образовательная: выработать прочные навыки решения систем двух уравнений с двумя неизвестными, способствовать совершенствованию полученных знаний по данной теме;

• развивающая: развитие внимания и логического мышления, памяти, активизация самостоятельной деятельности;

• воспитательная: способствовать развитию творческой деятельности учащихся, любознательности.

Оборудование: персональный компьютер, проектор, экран, раздаточный материал.

Методы работы:

• методы организации учебно-познавательной деятельности: словесный, наглядный, практический, самостоятельная работа;

• методы контроля и самоконтроля: устный опрос, фронтальный опрос, письменный опрос.

Ход урока

1. Организационный момент (3 мин)

Учитель приветствует учащихся, проводит проверку готовности класса к уроку, отмечает отсутствующих.

Демонстрация темы урока на экране. (Слайд № 1)

Эпиграф к теме:

«Метод решения хорош, если с самого начала мы можем предвидеть — и далее подтвердить это, — что, следуя этому методу, мы достигнем цели.»
Г.Лейбниц

Учитель:

Сегодня мы продолжим изучение темы «Системы линейных уравнений с двумя переменными». С чем вы познакомились на предыдущих уроках? (Учащиеся отвечают).

Итак, ранее вы познакомились с тремя способами решения систем линейных уравнений с двумя переменными (графический, метод подстановки и метод алгебраического сложения). Сегодня мы должны повторить способы решения систем двух линейных уравнений с двумя переменными; обобщить и систематизировать знания по данной теме; научиться выбирать методы решения каждой конкретной системы линейных уравнений.

Напоминаю, что систему можно решать любым из трех способов, который вам больше нравится, но лучше выбирать тот, что приведет к точному ответу быстрее, т.е. рациональный способ решения данной конкретной системы.

Сегодня на уроке повторяем методы решения систем уравнений с двумя переменными, решение задач с помощью систем уравнений с двумя переменными, а также примерных заданий ГИА. На уроке вы будете работать коллективно, самостоятельно, выполняя задания теста.

Учащиеся. Записывают в тетрадях число и тему урока.

2. Фронтальная работа с классом (5 мин).

1. Слайд № 2

Какая из пар является решением системы:

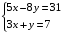
а) (4; −5) б) (2; 1) в) (3; −2) Ответ: в

Учитель. Что называется решением системы двух линейных уравнений с двумя переменными?

Ответ учащихся. Пару значений (x; y), которая одновременно является решением и первого, и второго уравнений системы, называют решением системы.

2. Слайд № 3

При решении задачи было введено обозначение x – количество мальчиков в классе, y – количество девочек. Какая из приведенных пар чисел может быть решением задачи?

1) ( ─ 5; 17) 2) ( ─ 5; ─ 17) 3) (5; ─ 17) 4) (5; 17)

Ответ: 4

3. Слайд № 4

На координатной плоскости построены графики функций y=−x−3 и y=4x+2. Используя эти графики, решите систему уравнений

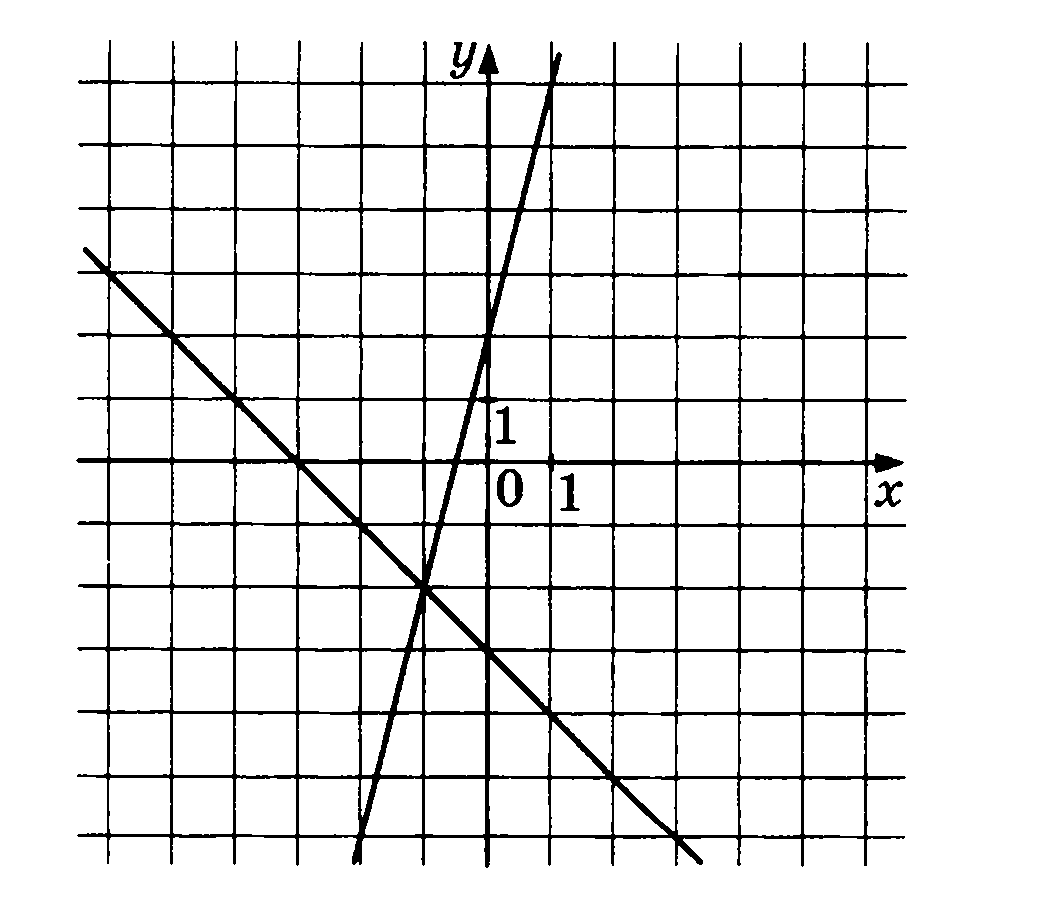
Ответ: (− 1; −2)

Учитель: Сколько решений может иметь система двух линейных уравнений с двумя переменными, от чего это зависит?

Ответ учащихся: единственное решение (прямые пересекаются), множество решений (прямые совпадают), не иметь решений (прямые параллельны).

Учитель. Какие методы решения систем двух линейных уравнений с двумя переменными существуют?

Ответ учащихся: Метод подстановки, метод алгебраического сложения, графический метод (слайд № 5).

Учитель. Как вы считаете, какой из методов наименее универсален и почему?

Ответ учащихся. Графический метод, т. к. в этом случае не всегда получается точное решение.

Учитель. Вспомним алгоритм решения системы уравнений графическим способом.

Демонстрация флэш-ролика. (слайд № 5).

3. Работа по теме урока (15 мин).

1. Двое учащиеся у доски решают задания на применение метода подстановки и метода сложения (слайд № 6). Эти же задания класс выполняет по вариантам.

Вариант 1. Решить систему методом подстановки: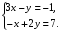

Ответ: (− 1; − 4).

Вариант 2. Решить систему методом сложения: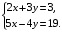

_{Ответ: (3; — 1).}

Учащиеся у доски комментируют решения.

Учитель. Есть ли другие ответы? Все ли согласны с решением?

2. Далее разбирается решение задания ГИА (совместное обсуждение), проверка решения – на слайде (слайд № 7).

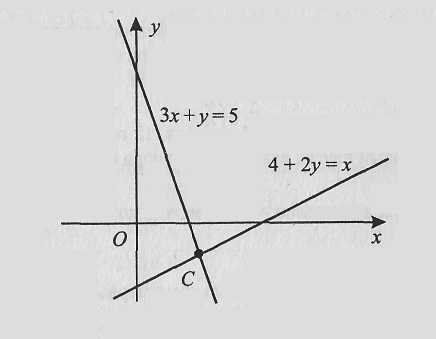
Две прямые пересекаются в точке А. Вычислите координаты точки А.

Ответ: (2: — 1).

3. Одновременно с решением предыдущего задания у доски один учащийся выполняет следующее задание.

Решить систему уравнений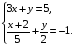

Учащийся комментирует свое решение. Ответ: (3; — 4)

4. Домашнее задание: стр. 79, домашняя контрольная работа № 3, № 2, 4, 6, 8 (по вариантам) (2 мин)

5. Проверочная работа в виде теста (10 мин).

В выданных бланках работ задания 1-4 с выбором ответа, необходимо обвести нужный вариант ответа. Задание 5 – с краткой записью ответа (решение на обороте). Работы необходимо подписать. У вас на партах также имеются бланки с таблицами для занесения верных ответов. Тест рассчитан на 10-12 мин. Работы вы должны сдать, а таблицы с выбранными ответами остаются у вас для последующей проверки.

6. Итоги урока (5 мин).

На экране демонстрируются верные ответы теста.

Поднимите руки те, кто набрал 3балла, 4 балла, 5 баллов.

По 1 баллу за работу на уроке добавляют (учитель называет фамилии учащихся, участвующих в работе в течении урока).

Критерии: 3балла – оценка «3»;

4 балла – оценка «4»;

5 баллов и выше – оценка «5».

Приложение 1

Тест по теме «Системы двух линейных уравнений с двумя переменными».

Ф. И. ________________________________ Класс ______________________

Вариант 1

1. На какое число необходимо умножить одно из уравнений системы 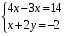так, чтобы с помощью сложения можно было исключить одну из переменных?

1) 4 2) – 4 3) 7 4) – 6.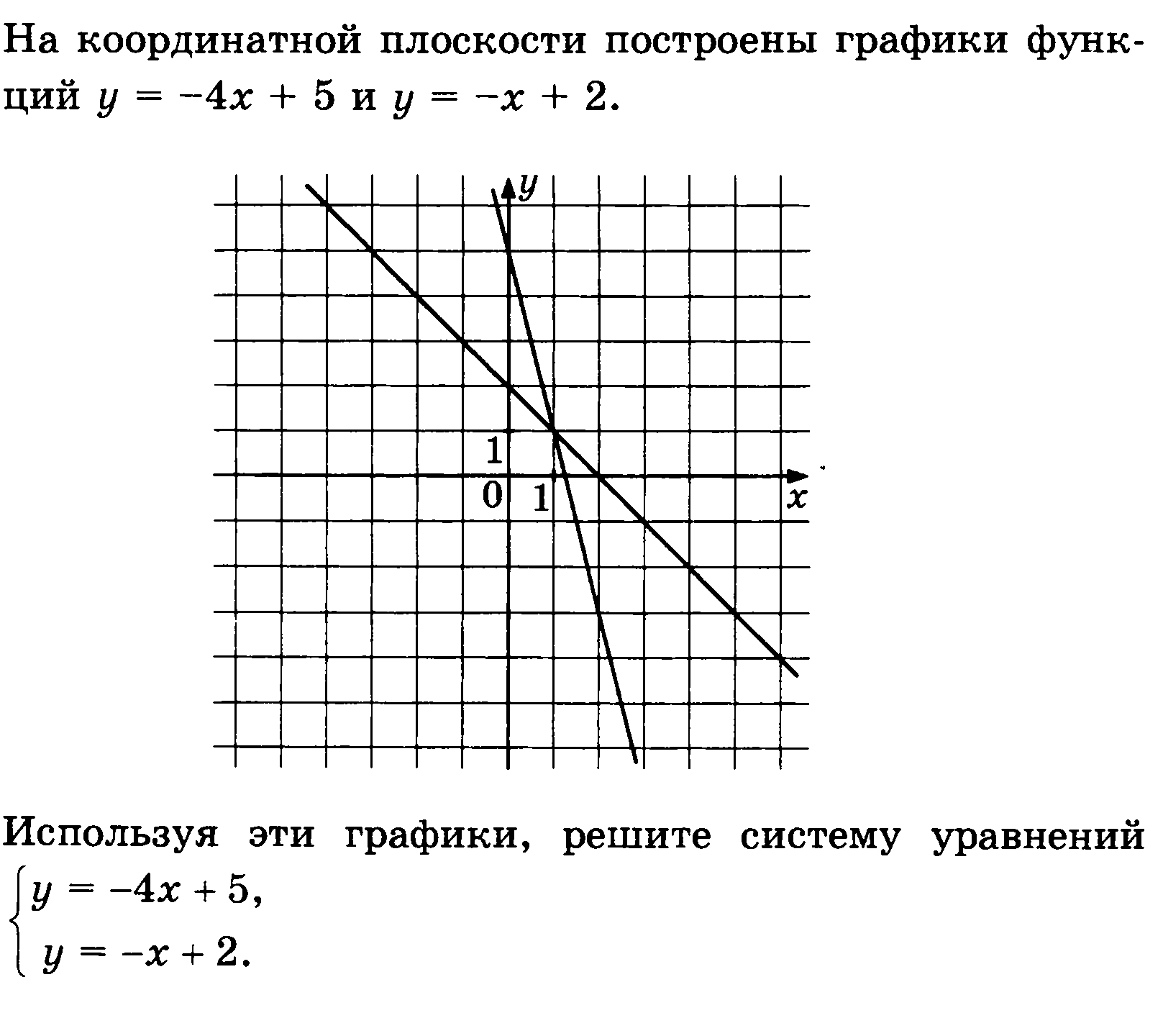

2. На координатной плоскости построены графики функци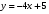й и 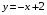. Используя эти графики, решите систему уравнений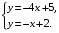

Ответ: ____________________

3. Укажите равенство, в котором правильно выполнена подстановка системы уравнений

1)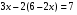 2)

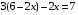
3) 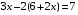4)

4. За три мороженых и две шоколадки Оля заплатила 75 рублей. Шоколадка дороже мороженого на 25 рублей. Какая система уравнений отвечает условию, если принять, что одно мороженое стоит x рублей, а шоколадка – y рублей?

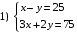
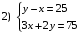
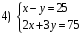
5. _{Решите систему уравнений}

Ответ: ______________________________________

Тест по теме «Системы двух линейных уравнений с двумя переменными».

Ф. И. ________________________________ Класс ______________________

Вариант 2

1. На какое число необходимо умножить одно из уравнений системы так, чтобы с помощью сложения можно было исключить одну из переменных?

1) 5 2) – 5 3) 3 4) 2.

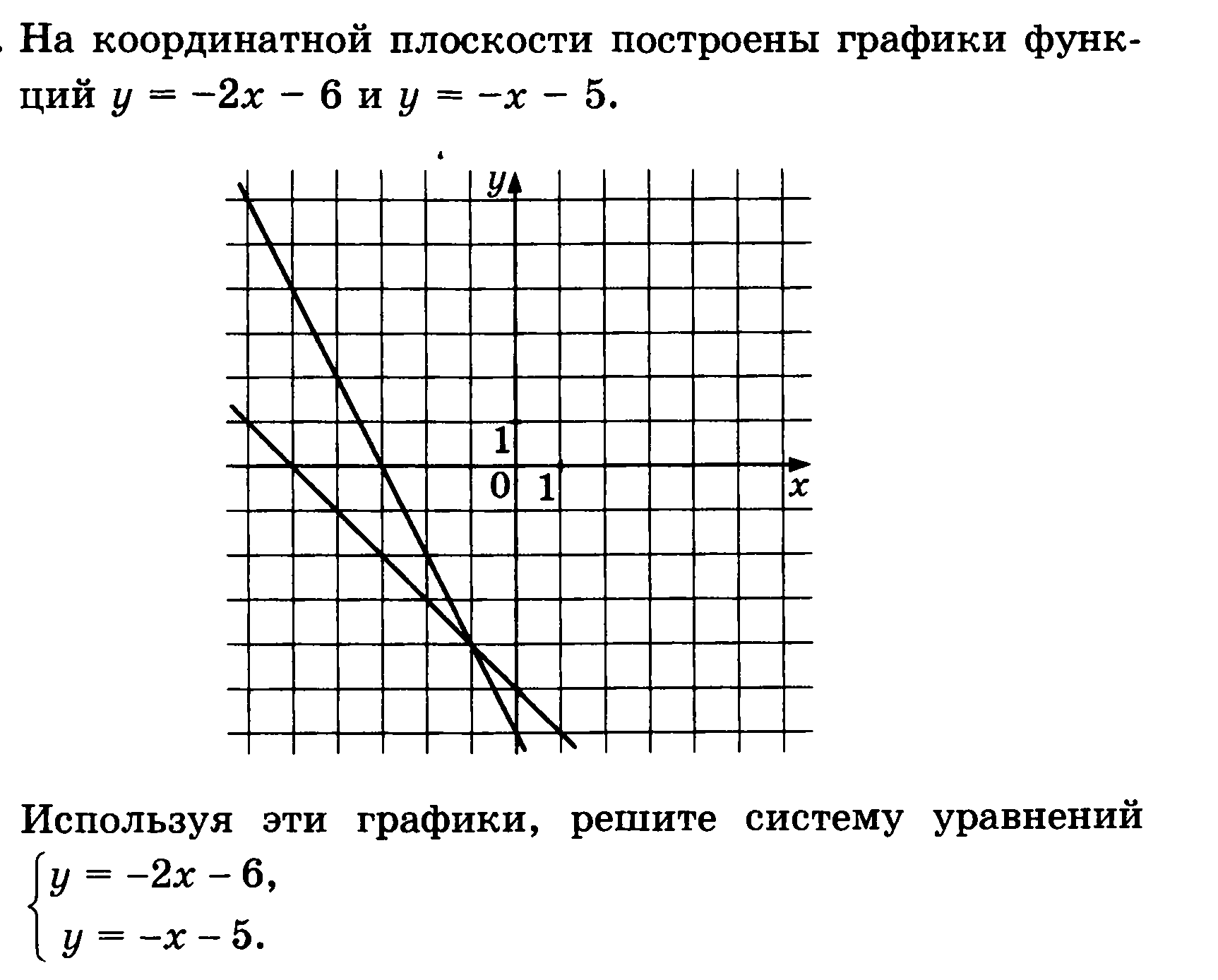
2. На координатной плоскости построены графики функций и 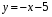. Используя эти графики, решите систему уравнений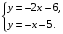

Ответ: ____________________

3. Укажите равенство, в котором правильно выполнена подстановка системы уравнений

1) 2)

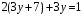
3) 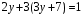4)

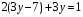
4. За 6 тетрадей и 2 обложки заплатили 98 рублей. Найдите цену одной тетради и одной обложки, если тетрадь дороже обложки на 11 рублей. Какая система уравнений отвечает условию, если принять, что одна обложка стоит x рублей, а тетрадь – y рублей?

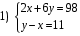
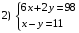
5. _{Решите систему уравнений}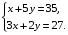

Ответ: ______________________________________

Приложение 2