Муниципальное общеобразовательное учреждение «Стрелецкая средняя общеобразовательная школа Белгородского района Белгородской области»
Открытый урок по математике
в 9 классе
Комбинаторика и космонавтика
Разработала: учитель физики
и математики
Базуева Вера Дмитриевна
2013 год
Урок по комбинаторике и статистике (Слайд 1)
«Комбинаторика и космонавтика»
Эпиграф к уроку: (Слайд 2)
«Не нужно нам владеть клинком,
Не ищем славы громкой.
Тот побеждает, кто знаком
С искусством мыслить тонко».
Уильям Уордсворд
Цели урока:
Повторение и обобщение знаний учащихся по разделам: «Статистические характеристики», «Статистические исследования», «Комбинаторика»;
формирование у обучающихся умения получать, воспринимать, анализировать и обрабатывать информацию, представленную в различных формах;
развитие познавательного интереса учащихся;
воспитание чувства патриотизма.
Формы организации учебного процесса деятельности: работа в парах, групповая, коллективная.
Ход урока:
Учитель: (Слайд 3). Возможно, вы встречали в литературе термин «прикладная математика» и задавались вопросом «Что же это такое?». Прикладная математика – область математики, рассматривающая применение математических методов, алгоритмов в других областях науки и практики». Одной из областей, где прикладная математика сыграла и продолжает играть огромную роль является космонавтика. Кроме теоретического исследования и расчета конструкции ракеты, математика необходима в течение всего космического полета. Так, например, траектория движения корабля описывается математическими формулами, в основе этого описания лежит такое математическое понятие, как система координат, а в основе обработки данных о траектории лежит понятие математической статистики.
Однозначное определение и прогнозирование положения тела в пространстве необходимы для управления полетом, можно свести к точным математическим алгоритмам. Создание современной технологии производства и запуска космических кораблей – итог труда многих ученых и инженеров, тем не менее, одну из ведущих ролей здесь играют специалисты, занимающиеся прикладной математикой. С одним из разделов прикладной математики мы знакомимся в школе. Это элементы статистики, теории вероятностей и комбинаторика.
Я просила вас дома подготовить небольшое сообщение об истории развития комбинаторики. Кто готов?
История: Комбинаторика является древнейшей наукой. Некоторые комбинаторные задачи решали еще в Индии во 2 веке до нашей эры, в древнем Китае, в Римской империи. Термин комбинаторика происходит от латинского слова «комбина», что в переводе на русский язык — «сочетать», «соединять». Элементарные сведения комбинаторного характера были известны очень давно, но они носили разрозненный характер. Определенный вклад в их систематизацию был сделан в 17 веке Блезом Паскалем и Пьером Ферма. В том же 17 веке попытку рассмотреть комбинаторику как единую теоретическую дисциплину предпринял Готфрид Лейбниц. (Слайд 4) Он отводил комбинаторике роль универсального математического аппарата логических рассуждений, кроме того, именно Лейбниц ввел в математику термин «комбинаторика». Немало для развития математики в целом и комбинаторики в частности сделали такие ученые как Рене Декарт, Леонард Эйлер и Даниил Бернулли. В результате деятельности таких крупных математиков комбинаторика получила успешное развитие, в это время были получены почти все формулы современной комбинаторики.
Учитель. Повторим основные понятия статистики и комбинаторики.
Фронтальный опрос:
Как называется число, наиболее часто встречающееся в данном ряду?
Ответ: Мода
Понятие моды относится не только к числовым рядам. (Слайд 5) Следующий ряд составлен из кличек животных: Шарик, Тузик, Полкан, Белка, Жучка, Стрелка, Стрелка, Шарик, Белка, Мухтар, Белка, Стрелка. Определить моду ряда.
Ответ: Белка и Стрелка. Чем знамениты эти собаки? (Слайд 6)
Как называется разность между наибольшим и наименьшим из чисел ряда?
Ответ: Размах.
На орбитальной станции «Мир» совершено 78 выходов в открытый космос. (Слайд 7). В выходах участвовали: 29 российских космонавта, 3 астронавта из США, 2- из Франции, 1 астронавт из Германии. Суммарную длительность пребывания в открытом космосе каждого космонавта можно представить в виде ряда (Слайд 8).
77ч46мин; 41ч59мин; 31ч48мин; 44ч00мин; 38ч33мин; 36ч29мин; 34ч32мин; 32ч17мин; 30ч30мин; 30ч30мин; 21ч54мин; 19ч39мин; 19ч11мин. Определите размах ряда.
Что такое медиана ряда чисел?
Ответ: Если число членов упорядоченного ряда нечетное, то это среднее число. Если число ряда нечетное, то это среднее арифметическое двух чисел записанных посредине.
Определить медиану ряда. Рост первых космонавтов: (Слайд 9)
Юрий Гагарин – 168см
Герман Титов – 169см
Андриан Николаев – 169см
Павел Попович – 168см
Григорий Нелюбов – 170см
Валерий Быковский – 167 см.
Ответ: 168,5см
(Слайд 10) В СССР отбор первых космонавтов в 1960 году можно было пройти, если твой возраст не превышал 30 лет, вес — 72 кг, а рост — 170 см. Только при таких характеристиках космонавт мог поместиться в первом космическом корабле “Восток”. Сейчас для кораблей “Союз — ТМА” требования не столь жесткие: рост стоя —150-190 см, рост сидя — 80-99 см, вес — 50-95 кг.
А как найти среднее арифметическое ряда чисел?
Ответ: Это частное от деления суммы чисел на их количество.
Статические данные иногда необходимо наглядно представить. В виде чего может это быть?
Ответ: В виде диаграмм и графиков.
Какие виды диаграмм вы знаете:
Ответ: Столбчатые и круговые.
Перед вами круговая диаграмма. (Слайд 11) На ней показано распределение по странам запуска искусственных спутников Земли в 2008 году. Всего было запущено 100 спутников. Определите в порядке убывания сколько спутников запустила каждая страна.
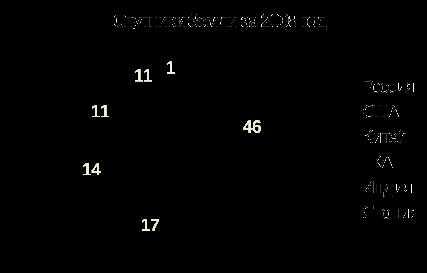
Кстати, скажите мне, какая страна запустила первый искусственный спутник, и в каком году? Назовите фамилию конструктора.
Ответ: СССР, в 1957 году. Конструктор С.П.Королев. (Слайд 12)
Какими способами рассуждений можно воспользоваться при решении некоторых комбинаторных задач?
Ответ: Перебор возможных вариантов, дерево возможных вариантов и комбинаторное правило умножения.
Что называется перестановкой из n-элементов? Ответ: Перестановкой из n-элементов называют всяких упорядоченный набор из этих элементов.
Как обозначают?
Ответ: Рn = n!
А что такое n!?
Ответ: Это произведение натуральных чисел от 1 до n.
Дать определение размещению.
Ответ: Размещением из n элементов по к (к меньше или равно n) называют любое множество, состоящее из к-элементов, взятых в определенном порядке из данных n-элементов. Формула размещения: Аnk = n!/(n-k)!
Чему равно 0!? Аnn?
Что называется сочетанием?
Ответ: Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов.
Формула: Сnk = n!/(k!(n—k)!
Что называется относительной частотой случайного события?
Ответ: Относительной частотой случайного события в серии испытаний называется отношение числа испытаний, в которых это событие наступило, к числу всех испытаний. (m/n).
Что называется вероятностью равновозможных событий?
Ответ: Если все исходы события равновозможные, то вероятность события равна отношению благоприятных исходов к числу всех исходов. (Р(А))
Устный счет. (Слайд 13)
1. Делится ли число 30! на:
а) 90 б) 92 в) 94
2. Найти значение выражения: Ответ а)15, б) 1/90, в) 40
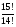
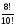
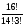
а) б) в)
3. Что больше: 6! · 5 или 5! · 6
А сейчас решим некоторые комбинаторные задачи, связанные с космосом.
(Слайд 14) Многих интересует вопрос: а что едят космонавты на борту космической станции. Разработка продуктов питания для космонавтов еще в 1963 году стала производиться институтом питания РАН. Тогда господствовала точка зрения, что продукты, употребляемые в космосе должны кардинально отличаться от земных и формой и консистенцией. Идеальной пищей могли бы стать питательные таблетки, полностью усваиваемые организмом. Но таких таблеток создать не удалось. Космические обеды запечатывались в тубы и могли быть высосаны прямо из нее. На орбите современные космонавты едят практически все тоже самое, что и на родной планете. Ставшие символом космического питания тюбики сейчас используют редко – пищу в основном расфасовывают по банкам.
Решите задачу: (Слайд 15)На борту космического корабля предлагается космонавтам в тубах питание: на 1 – борщ с мясом, рассольник и суп-харчо. На 2 — цыплята с рисом, судак в соусе, поджарка с мясом и овощами, говядина под майонезом, картофельное пюре. Набор напитков таков: кофе, чай черный, чай зеленый, молоко и сок. Сколько выбора у космонавтов обеда из трех блюд?
Ответ: Правило комбинаторного умножения.
3*5* 5= 75 вариантов
Космическая станция напоминает сразу и дом, и лабораторию, и машину, до отказа наполненную разнообразной техникой. Главное помещение станции – основной отсек – представляет собой два цилиндра разных диаметров, соединенных между собой конусом. В малом цилиндре располагаются рабочие места космонавтов и центральный пульт управления станцией. В конусе – «стадион» — оборудования для тренировки. При длительном полете приходится тренироваться каждый день, иначе мышцы космонавтов ослабеют. В большом цилиндре расположен холодильник, хранятся запасы пищи и воды, здесь же располагаются и спальные места. На ночь каждый космонавт укладывается в персональный спальный мешок и пристегивается ремнем.
А сейчас решите задачу. За пультом управления 5 рабочих мест.
а) Сколько способов есть у 5 космонавтов, чтобы занять места.
Ответ: 5!=120
б) Сколько способов существует при условии, что командир и зам.командира должны сидеть рядом?
Ответ: Чтобы решить эту задачу нужно применить комбинаторное правило умножения и правило перестановки.
5*2*3!= 60 способов.
Из 8-ми членов команды космонавтов надо выбрать командира и его заместителя. Сколько способов существует?
Ответ: С82= 28
Космическая станция.
На космической станции «Мир» побывали 104 космонавта из 12 стран мира. Рассчитайте сколькими способами можно отправить космонавтов на станцию из 8 стран, если на ней могут разместиться 5 космонавтов? С каждой страны можно взять по одному космонавту.
Ответ: Число размещений А85 =6720 способов
(Слайд 16). Первый выход в открытый космос был совершён советским космонавтом Алексеем Архиповичем Леоновым 18 марта 1965 года с борта космического корабля «Восход-2» с использованием гибкой шлюзовой камеры. За 40 лет истории выходов и работы в открытом космосе — специалисты называют её внекорабельной деятельностью — продолжительность пребывания человека в космическом вакууме за один выход выросла от 12 минут до 9 часов.
Из космической станции надо, чтобы три человека вышли в открытый космос. Всего на борту 5 космонавтов и командир корабля.
Сколько способов имеется, чтобы это можно было сделать?
а) если командир корабля должен выйти в открытый космос
б) если командир корабля должен остаться
Ответ:
а) Командир выходит в космос, значит, с ним могут выйти еще двое из 5. С52 = 10 способов
б) Командир остается, значит, С53 =30 способов.
31.Многие космонавты мечтали полететь в космос вместе с Гагариным.
32.Заявки на полет в космос подали 26 космонавтов, из них 14 из России. В полет должны отправиться двое космонавтов. Кто полетит — выбирает жребий. Обязательно полетит космонавт Ю.А.Гагарин. Какова вероятность того, что Гагарин полетит с кем-нибудь из России?
Ответ: 0,52
Мы с вами повторили основные вопросы статистики и комбинаторики, а теперь небольшой тест.
Ответы на тест (Слайд 17)
В будущем человечество, конечно, освоит Луну. Может и на Марсе будут яблони цвести. Очень возможно, что удастся посетить крупные спутники Юпитера или Сатурна, но это осуществить сможет уже ваше поколение, вот почему вам так необходимы знания из различных областей науки, в том числе и прикладная математика.
Д/З. п. 35. №808, 809,817.
(Слайд 18). До свидания.
Тест по комбинаторике
Вариант 1.
Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков?
1) 30 2) 100 3) 120 4) 5
2. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?
1) 10 2) 60 3) 20 4) 30
3. Аня решила сварить компот из фруктов 2-ух видов. Сколько различных вариантов (по сочетанию фруктов) компотов может сварить Аня, если у нее имеется 7 видов фруктов?
1) 14 2) 10 3) 21 4) 30
4. Вычислить: 6! -5!
1) 600 2) 300 3) 1 4) 1000
5. В ящике лежат карточки с буквами, из которых можно составить слово «космонавтика». Какова вероятность того, что наугад выбранная буква окажется буквой к?
1) 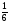 2) 6 3)
2) 6 3) 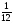 4)
4) 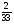
| 1 | 2 | 3 | 4 | 5 | |
| № ответа
| 3 | 4 | 3 | 1 | 1 |
Вариант 2.
Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?
1) 100 2) 30 3) 5 4) 120
2. В футбольной команде 11 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать?
1) 22 2) 11 3) 110 4) 15
На полке стоят 12 книг. Наде надо взять 5 книг. Сколькими способами она может это сделать?
1) 792 2) 17 3) 60 4) 300
4. Вычислите: 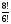
1) 2 2) 56 3) 30 4) 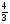
5. В ящике лежат карточки с буквами, из которых можно составить слово «комбинаторика». Какова вероятность того, что наугад выбранная буква окажется буквой к?
1) 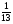 2) 13 3)
2) 13 3) 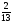 4)
4) 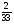
| 1 | 2 | 3 | 4 | 5 | |
| № ответа
| 4 | 3 | 1 | 2 | 3 |
Список литературы:
1. Н.Я. Виленкин, А.Н. Виленкин, П.А. Виленкин. Комбинаторика. М., 2006.
2. В.Е. Гмурман. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1975.
3. И.И.Ежов, А.В.Скороход, М.И.Ядренко. Элементы комбинаторики. М., 1977.
государственный педагогический институт
4. «Введение в комбинаторику», Колотова И.В., г. Саратов.
