Конспект урока на тему «Квадратные корни. Арифметический квадратный корень»

Время мин

Формы организации учебной деятельности

Деятельность учителя

Деятельность обучающихся

Формирование УУД

1.Орг. момент

2-3 мин

Учитель приветствует учеников:

«Придумано кем-то просто и мудро

При встрече здороваться: Доброе утро!

Доброе утро солнцу и птицам!

Доброе утро улыбчивым лицам!

Каждый становиться мудрым, доверчивым.

И доброе утро длится до вечера.

Здравствуйте, ребята, садитесь».

Сегодня у нас урок необычный, к нам пришли гости, а девизом нашего урока станут слова китайской притчи: «Скажи мне- и я забуду,

Покажи мне — и я запомню,

Дай сделать – и я пойму».(Слайд№1)

Приветствуют учителя

Личностные УУД:

Развитие познавательных интересов, учебных мотивов, формирования мотивов достижения и социального признания, мотива, реализующего потребность в социально значимой и социально оцениваемой деятельности.

2.Объявление темы урока и постановка целей

2 мин

Ребята, отгадайте загадку:

Он есть у дерева, цветка,

он есть у уравнений.

И знак особый- радикал,

с ним связан вне сомнений

Заданий многих он итог,

И с этим мы не спорим

Надеемся, что каждый смог

ответить: это…(корень)

Какова тема нашего урока?

Какие цели и задачи мы поставим перед собой?

Учащиеся называют тему и цели урока.

(Слайд №2)

Тема: «Арифметический квадратный корень»

Цели:

1.Повторить, что такое арифметический квадратный корень?

2.Закрепить умения применять определение, свойства арифметического квадратного корня.

(Слайд 3)

Регулятивные УУД:

целеполагание, планирование, саморегуляция.

3 Устный счёт.

5мин

(Слайд 4)

-Что такое квадратный корень?

-Что называется арифметическим квадратным корнем?

-Как называется выражение, стоящее под знаком корня?

-При каких значениях а имеет смысл выражение √а?

-Объясните, почему верно или неверно равенство:

√0,64=0,8 (равенство верно, т.к.0,8>0 и 0,8² = 0,64)

√0,25= — 0,5 (равенство неверно, т.к.

-0,5<0)

— Вычислить арифметический квадратный корень из чисел: √900;√0,36; √25; √0,04,

Учащиеся отвечают на вопросы.

—Квадратным корнем из числа а называется число, квадрат которого равен а.

—Арифметическим квадратнымкорнем из числа а называется неотрицательное число, квадрат которого равен а.

-Выражение, стоящее под знаком корня называется подкоренным выражением.

-Выражение √а имеет смысл при а ≥0.

30; 0,6; 5;0,2;9.

Коммуникативные УУД:

умение с достаточной полнотой и точностью выражать свои мысли.

Метапредметные результаты:

Формирование умений воспринимать и перерабатывать информацию и представлять её в словесной форме, умение давать полные ответы.

4.Актуализация знаний учащихся.

10-13мин

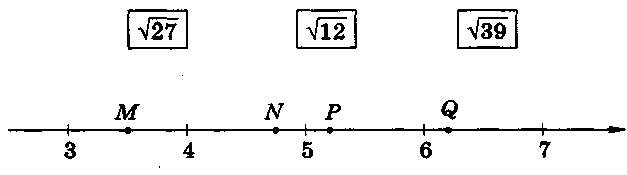
-Тест(раздается каждому ученику)

-Сможете ли вы, имея полученные знания об арифметическом квадратном корне, выполнить задание из сборника для подготовки к ГИА? (Слайд 6)

-Каждое из чисел√ 27,√13,√39 соотнесите с соответствующей ему точкой координатной прямой. (Работа в парах)

-Повторим пройденное.

-Разгадай кроссворд (радикал)

(работа по рядам)

Ответы на тест:

1 вариант

А1-3,А2-1,А3-2,А4-3,В1-8.

2 вариант

А1-4, А2-3, А3-1,А4-2,В1-5.

(Слайд 5)

√27-P, √12-M, √39-Q.

Познавательные УУД:

логические действия

(анализ условия задания, установление причинно-следственных связей в получении результатов)

Коммуникативные УУД:

работа в группах,

умение с достаточной полнотой и точностью выражать свои мысли.

Метапредметные результаты:

Формирование умений воспринимать и перерабатывать информацию и представлять её в словесной форме, овладение навыками планирования и оценки результатов своей деятельности

5. «Из истории математики»

5мин

История возникновения знака корня?

Историческая справка.

Один из учащихся представляет историческую справку.

(Слайд№7)

Коммуникативные УУД:

умение с достаточной полнотой и точностью выражать свои мысли.

6.Физминут-ка

1мин

(Слайд 8)Электронная физминутка для глаз.

Учащиеся выполняют упражнения.

7. Редактирование памяток.

3 мин

(Работа по диагонали)

7. Самостоятельная работа

(разноуровневые задания)

10мин

Объяснение правил выполнения самостоятельной работы.

(Слайд№9)

Ученики выбирают уровень сложности самостоятельной работы и самостоятельно выполняют задания (тесты), отмечают в тетрадях правильные ответы.

Предметные результаты:

умение получать и применять полученные знания при решении задач.

8. Взаимо-проверка

2мин

Уровень 1 за каждый правильный ответ 1 балл

Уровень 2 за каждый правильный ответ 2 балла

Уровень 3 за каждый правильный ответ 3 балла

Проводят взаимопроверку. Правильные ответы на доске (Слайд10).

9. Подведение итогов. Выставление оценок по результатам набранных баллов за урок.

Самооценивание.

2 мин

Выставление оценок по результатам набранных баллов за урок.

-Итак, чем же мы с вами занимались сегодня на уроке?

-Чему вы научились сегодня на уроке?

-Где вам могут пригодиться эти знания?

-Каким образом наш урок связан с китайской притчей?

— Продолжите одну из фраз.

(Слайд 11)

1. Сегодня я узнал…

2. Было интересно, потому что…

3. Было трудно, потому что…

4. Я понял, что…

5. Смогу помочь другу…

6. Теперь я могу…

7. Я научился…

Подсчёт баллов

Выставление оценок по результатам набранных баллов за урок.

Отвечают на вопросы учителя.

10. Постановка домашнего задания

1 мин

Постановка домашнего задания (дифференцированное)

(Слайд 12)

Записывают домашнее задание

Имя

этапы

задания

количество баллов

I

Устный счёт

(за каждый правильный ответ 1 балл)

II

Тестирование (работа по вариантам)

(за каждый правильный ответ 1 балл)

Повторим пройденное.

(Индивидуальная работа)

(за каждый правильный ответ 1 балл)

Задание из сборника к ГИА. (Работа в парах)

(за правильный ответ 2балла)

Разгадай кроссворд.(Работа в группах)

(за каждое верное слово 1 балл)

Индивидуальное задание.(Памятка)

IV

Самостоятельная работа (тест)

(разноуровневые задания)

Уровень 1: за каждый правильный ответ 1 балл

Уровень 2: за каждый правильный ответ 2 балла

Уровень 3: за каждый правильный ответ 3 балла

Итоговое количество баллов

Оценка

Количество баллов 20 и более — оценка «5»

Количество баллов 12-19 — оценка «4»

Количество баллов 5-11 — оценка «3»

Количество баллов менее 4 оценка «2»

Уровень 1

Оценка «3»

1.Какое выражение не имеет смысла?

А) В) С) Д)

2.Найдите значение корня -√81

А) 18 В) — 9 С) 36 Д) 324

3.Вычислите √26+в, если в=10

А) 216 В) С) 12 Д) 6

4.Решите уравнение

А) 25 В) — 25 С) 25; — 25 Д) не имеет корня

5.Найдите значение выражения — √9 * √121

А) 22 В) 33 С) -33 Д) 0

Уровень 2

Оценка «4»

1.Найдите значение корня

А) В) С) Д)

2.Найдите значение выражения — √0,01 — √0,36

А) 0,5 В) -5 С) – 0,5 Д) – 0,7

3.Выполните действия х- 3√х при х=9

А) 0 В) 1 С) -1 Д) 0,5

4.При каких значениях уверно равенство 6√у=6

А) -1 В) 36 С) 1 Д) 0

5. Решите уравнение

А) 121 В) — 121 С) 121; — 121 Д) не имеет корня

Уровень 3

Оценка «5»

1.Найдите значение выражения 2√х – х при х=0,36

А) 7,2 В) -0,84 С) 0,84 Д) 0

2.Найдите значение корня √

А) В) С) Д) нельзя извлечь

3.При каком значении х верно равенство √х – 6 =0

A)1B) 36C) 6Д) -6

4.Найдите значение выражения

А) 0 В) 0,7 С) – 0,7 Д) — 3

5.При каких значениях х имеет смысл выражение √7х

А) при х>0 В) при х=0 С) при х< 0 Д) при х≥ 0

2

3

4

5

6

7

Памятка №2

В день можно съедать не более √ кг сладостей, дневная норма потребления хлеба составляет √ кг, сливочного масла √ кг.

На компьютере рекомендуется работать не более √400 минут, а потом необходима зарядка для глаз, по сотовым телефонам нужно разговаривать не более √1600 секунд, смотреть телевизор не более √4часов.

2

3

4

5

6

7