Урок-соревнование
по разделу
«Решение задач по теме «Элементы комбинаторики, статистики и теории вероятности»
г.Новороссийск, 2013
Цели урока:
в нетрадиционной, занимательной форме повторить и закрепить пройденный материал по теме;
развивать познавательную активность и творчество студентов;
развивать и закреплять навыки решения задач;
учить применять знания в новой ситуации;
формировать навыки коллективной работы в сочетании с самостоятельной деятельностью учащихся;
формировать навыки работы на уроке в офлайн режиме.
Оборудование: мультимедийный проектор, карточки с заданиями к конкурсам.
Ход урока.
Оргмомент – 5 мин.
Предварительно учащиеся делятся на 2 команды, выбирают капитана и название. Заранее готовится ведомость, в которую жюри (или учитель) будут вносить оценки за каждый ответ каждому учащемуся. В итоге побеждает команда, набравшая больше баллов.
Сам урок состоит из нескольких конкурсов. (40 минут)
1. Конкурс «Знаешь ли ты формулы?».
На доске написаны цифры. Представители команд по очереди выбирают цифру; выпавшую формулу записывает учитель на доске, поясняют ее назначение. За каждый правильный ответ ученик, а следовательно, его команда получает по баллу. Если ученик отвечает неправильно, право объяснить формулу переходит к команде-сопернице с дополнительным баллом.
Задания к конкурсу:
1) 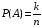 — классическое определение вероятности
— классическое определение вероятности
2) 0≤Р(А)≤1 Вероятность события всегда больше 0 и меньше 1.
3) Р(А) = 1 Вероятность достоверного события равна 1.
4) 5) 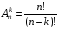 — размещение из n элементов по k элементов
— размещение из n элементов по k элементов
5) 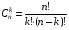 — сочетание из n элементов по k элементов
— сочетание из n элементов по k элементов
6)  — перестановки из n элементов
— перестановки из n элементов
2. Конкурс смекалистых.
Конкурс посвящается решению задач. Каждая команда получает 9 несложных задач.. На конкурс отводится 6-7 минут. За каждую решенную правильно задачу команда получает 1 балл. Еще один балл получает команда, которая решила все задачи (при условии, что все они решены правильно).
Задания к конкурсу:
Из урны, в которой находятся 3 белых, 4 черных, 5 красных шаров, наудачу вынимается один. Какова вероятность того, что вынутый шар окажется белым? (Ответ: 1/4)
Брошена игральная кость. Найти вероятность того, что выпадет четное число очков? (Ответ: 1/2)
В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный? (Ответ: 200/1000 = 0,2)
Найти вероятность того, что при подбрасывании игральной кости выпадет число очков меньше 7. (Ответ: 1)
Из урны, в которой находятся 8 шаров: 3 белых и 5 красных, наудачу вынимается один. Какова вероятность того, что вынутый шар окажется зеленым? (Ответ: 0)
Найти вероятность того, что при бросании игральной кости выпадет число очков, кратное 3. (Ответ:1/3)
Из слова «автоматика» выбирается наугад одна буква. Какова вероятность того, что эта буква «а»? (Ответ: 0,3)
На завод привезли партию из 1000 подшипников. Случайно в эту партию попало 30 подшипников, не удовлетворяющих стандарту. Определить вероятность P(A) того, что взятый наудачу подшипник окажется стандартным. P(A)=M/N=970/1000=0.97
Группа учащихся изучает 7 учебных дисциплин. Сколькими способами можно составить расписание занятий в понедельник, если в этот день недели должно быть 3 различных урока? (Ответ: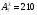 )
)
3. Конкурс капитанов.
Капитаны садятся за отдельный стол и решают по одной задаче. Первый выполнивший задание правильно получает 1 балл. Если капитан не знает как решить задачу, он может воспользоваться помощью команды. Т.е. команда тоже должна решать эту задачу, чтобы в любой момент оказать помощь своему капитану. Решение задачи должно быть с объяснением.
Задания к конкурсу:
Продавец записывал вес дынь, которые он продавал, округляя до целых. Запись выглядит так: 5, 3, 2, 5, 4, 7, 9, 3, 2, 2, 2, 6, 7, 8, 13.
Найти размах, моду, медиану.
(размах: 13-2=9, мода:2, медиана: 3)
Продавец записывал вес дынь, которые он продавал, округляя до целых. Запись выглядит так: 4, 10, 15, 5, 2, 3, 5, 3, 3, 3, 3, 4, 9, 1, 13.
Найти размах, моду, медиану.
(размах: 15-2=13, мода:3, медиана: 3)
4. Конкурс «Поиск» (проводится в то время пока капитаны решают задачи).
Конкурс является домашним заданием. Команды заранее получили задание — найти в журналах, книгах интересные факты, касающиеся темы «Теория вероятностей», и подготовить небольшие сообщения (не более 2-3 мин). Команды получают 1 или 2 балла (наиболее интересное сообщение оценивается 2 баллами). Если оба сообщения интересны, то команды получают по 2 балла.
5. Конкурс «Ты мне, я тебе»
Конкурс вопросов. На доске геометрические фигуры. За каждой фигурой есть вопрос., который адресуется команде-сопернице. За каждый правильный ответ команда получает по 1 баллу. Если ответа правильного нет, команда, которая сама задавала вопрос должна на него ответить и заработать 1 балл.
Примерные вопросы конкурса:
Что такое случайное событие? (Под случайным событием, связанным с н6екоторым опытом, понимается всякое событие, которое при осуществлении этого опыты либо происходит, либо не происходит.)
Какое событие называется достоверным? (Событие, всегда осуществляющееся при проведении опыта, называют достоверным событием)
Какое событие называется невозможным? (Невозможным называют событие, которое заведомо не может произойти в результате опыта)
Сформулировать классическое определение вероятности события? (Вероятностью события А, связанного с опытом с равновероятными исходами, называется отношение k/n числа элементарных событий, благоприятствующих событию А, к числу всех элементарных событий, т.е. 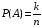 )
)
Чему равна вероятность достоверного события? (Вероятность достоверного события равна 1)
Чему равна вероятность невозможного события? (Вероятность невозможного события равна 0)
Что такое мода? (Мода – это варианта, которая встречалась чаще других)
Что такое размах? (Размах – это разность между максимальной и минимальной вариантами)
Что такое медиана? (Медиана – это после упорядочивания по возрастанию, варианта, стоящая в середине, если вариант нечетное количество, и среднее арифметическое двух средних вариант, если их четное количество)
Может ли быть две моды? (Да)
6. Конкурс «Реши задачу».
Конкурс решения более сложных задач. Все учащиеся индивидуально решают одну и ту же задачу. На решение отводится несколько минут. Первая правильно решившая задачу команда получает 1 балл.
Задание к конкурсу:
Сколькими способами можно составить график дежурства по классу (в классе 20 человек),если группа дежурных состоит из 2 учеников?
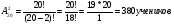
Подведение итогов (выступление членов жюри) – 5 мин.
Во время принятия решения жюри, учащиеся смотрят видеоролик.
Рефлексия.
— Кто себе поставит «5» поднимите руку.
— Кто себе поставит «4» поднимите руку.
— Кто себе поставит «3» поднимите руку.
— Кто себе поставит «2» поднимите руку.
Литература:
Богомолов Н.В., Самойленко П.И. Математика. – М.: Дрофа, 2006.
Яковлев Г.Н. Алгебра и начала анализа. Часть II. – М.: Наука, 1987.
Богомолов Н.В. Сборник дидактических заданий по математике. – М.: Дрофа, 2006
5
