«КВМ» по квадратным уравнениям
Урок-КВМ расчитан на 2 урока
Цели:
Образовательные : повторение различных способов решения квадратных уравнений, проверка умений верно и рационально решать квадратные уравнения, повторение квадратных корней и их свойств.
Развивающие: способствовать формированию умений обобщать, сравнивать, выделять главное, развивать математический кругозор, мышление, внимание и память.
Воспитательные: содействовать воспитанию интереса к математике.
Методическое обеспечение: электронная доска, ноутбук,медиапроектор, высказывание на плакате, ромашка, лепестки ромашки с уравнениями, карточки с уравнениями.
План урока:
1.Представление команд и жюри.
2.Устная разминка команд.
вычислить
конкурс теоретиков
конкурс на лучшего вычислителя.
3.Конкурс » Ромашка»
4. Работа по карточкам
5..Конкурс «Изюминка»
6.Подведение итогов.
7.Рефлексия.
Ход урока:
1.Представление команд.
1команда- «уравнения»
2команда-«корни»
3 команда-«дискриминант»
2.Устная разминка команд.
а) Вычислить
На электронной доске представлены задания командам. К доске выходят по одному представителю команды , решают задания и выбирают из предложенных ответов верные.
1команда 2 команда 3 команда
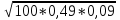




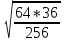

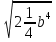

Варианты ответов:
2,1; 4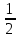 ;
;  a2 1,2; 2
a2 1,2; 2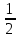 ; 1
; 1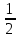 b2 0,8; 3; 1
b2 0,8; 3; 1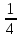 с25
с25
2,01; —  ; 2
; 2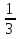 a2 1,02; —
a2 1,02; — 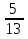 ; 2
; 2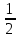 b2 0,08; —
b2 0,08; — 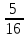 ; 1
; 1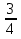 c2
c2
б)Конкурс теоретиков -задать командам по 2 вопроса (выполняется одновременно с заданием а).Вопросы на электронной доске.
1 команда
1.Дать определение квадратного уравнения..
2.В каком случае квадратное уравнение не имеет корней.
2 команда
1.Сформулировать теорему Виета.
2. В каком случае квадратное уравнение имеет два корня.
3 команда
1.Записать формулу дискриминанта и корней квадратного уравнения.
3.В каком случае квадратное уравнение имеет один корень.
в) Конкурс на лучшего вычислителя.
На доске записан пример, который команды решают вместе за своим столом.
( +
+ )*
)*
3.Конкурс «Ромашка»
На доске ромашка из 8 лепестков. На каждом лепестке приведенное квадратное уравнение. Каждому члену команды раздаю по одному лепестку .Необходимо решить все восемь уравнений по теореме Виета и найти сумму всех найденных корней., должно получится число, записанное на обратной стороне сердцевины.
Уравнения:
1) x2-7x+12=0 x=3;4.
2) x2+18x+32=0 x=-16;-2.
3 )x2-5x-14=0 x=-2;7.
4) x2+5x+6=0 x=-3;-2.
5) x2-8x+12=0 x=2;6.
6) x2-12x+11=0 x=1;11.
7) x2-7x+10=0 x=5;2.
8) x2+2x-8=0 x=-4;2.
3+4-16-2-2+7-3-2+2+6+1+11+5+2-4+2=14
4.Работа по карточкам под лозунгом «Дорогу осилит идущий, а математику- мыслящий»
Всем членам команды раздаются карточки с квадратным уравнением, которое надо решить. Жюри проверяет уравнения.
Уравнения:
1)2x2-16x=0 (8;0) 10) 2x2+16x=0 (-8;0)
2)5x2-50x=0 (10;0) 11) x2-12x+27=0 (9;3)
3)x2-4x-32=0 (8;-4) 12) 2x2-6x-56=0 (7;-4)
4) x2+12x+32=0 (-8;-4) 13) x2+9x+20=0 (-5;-4)
5)x2+11x-26=0 (-13;2) 14) x2+8x=0 (-8;0)
6) 5x2-40x=0 (8;0) 15) x2-14x+40=0 (4;10)
7) x2-11x+24=0 (8;3) 16) 3x2-18x+15=0 (1;5)
8) 4x2-12x-40=0 (-2;5) 17) 4x2-24x+32=0 (2;4)
9) 2x2+13x-24=0 (-8;15) 18)x2-3x+2,25=0 (1,5;1,5).
5.Конкурс «Изюминка»-другие способы решения квадратных уравнений.
Команды рассказывают о других способах решения квадратных уравнений.
Показывают свои презентации ( темы озвучиваются зараннее).
1) Графическое решение квадратное уравнения
Если в уравнении х2 + рх + q =
перенести второй и третий члены в правую часть, то получим х2 = — рх — q.
Построим графики зависимостей у = х2 и у = — рх — q.
График первой зависимости — парабола, проходящая через начало координат. График второй зависимости — прямая (рис. 1).
Возможны следующие случаи:
— прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
— прямая и парабола могут касаться (только одна общая точка), т. е. уравнение имеет одно решение;
— прямая и парабола не имеют общих точек, т. е. квадратное уравнение не имеет корней.
Примеры:
1. Решим графически уравнение х2 — 3х — 4 = 0 (рис. 2).
Решение. Запишем уравнение в виде х2 = 3х + 4. 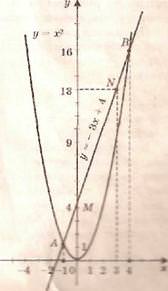
Построим параболу у = x2 и прямую у = 3х + 4. Прямую у = 3х + 4 можно построить по двум точкам М(0; 4) и N(3; 13). Прямая и парабола пересекаются в двух точках А и В с абсциссами х1 = — 1 и х2 = 4.
2) Решение квадратных уравнений с помощью циркуля и линейки
Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.
Предлагаем следующий способ нахождения корней квадратного уравнения
рис.1
ах2 + вх + с = 0
Допустим, что искомая окружность пересекает ось абсцисс в точках B(х1;0) и D(x2;0), где х1 и х2 — корни уравнения ах2 + вх +с =0,
и проходит через точки А(0; 1) и С(0; ![]() ) на оси ординат. Тогда по теореме о секущих имеем OB•OD = OA•ОС, откуда
) на оси ординат. Тогда по теореме о секущих имеем OB•OD = OA•ОС, откуда ![]()
Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд АС и BD, поэтому
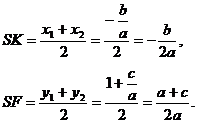
Итак: 1) построим точки ![]() (центр окружности) и А(0; 1);
(центр окружности) и А(0; 1);
2)проведем окружность с радиусом SA;
3)абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
1) Радиус окружности больше ординаты центра ![]() окружность пересекает ось ОХ в точке В(х1;0), и D(x1; 0), где х1 и х2 —корни квадратного уравнения ах2+bx+c= 0.
окружность пересекает ось ОХ в точке В(х1;0), и D(x1; 0), где х1 и х2 —корни квадратного уравнения ах2+bx+c= 0.
2) Радиус окружности равен ординате центра , окружность касается оси Ох в точке В(х1;0), где х1 — корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра ![]()
окружность не имеет общих точек с осью абсцисс (рис. 3), в этом случае уравнение не имеет решения.
|
|
рис.2. рис.3.
3) Решение квадратных уравнений с помощью номограммы.
Это старый и незаслуженно забытый способ решения квадратных уравнений z2 + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения
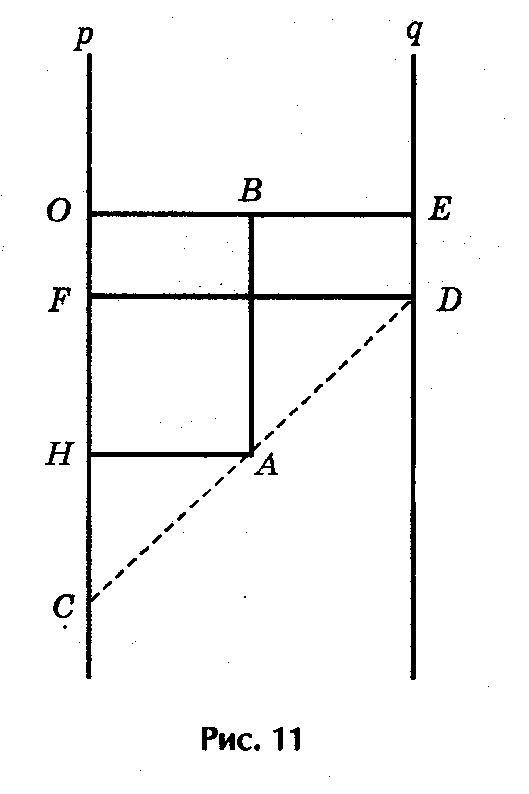
Криволинейная шкала номограммы построена по формулам (рис.11):
![]()
Полагая ОС = р, ED = q, ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию
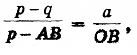
откуда после подстановок и упрощений вытекает уравнение z2 + pz + q = 0,
причем буква z означает метку любой точки криволинейной шкалы.
Примеры:
1) Для уравнения z2 — 9z + 8 = 0 номограмма дает корни
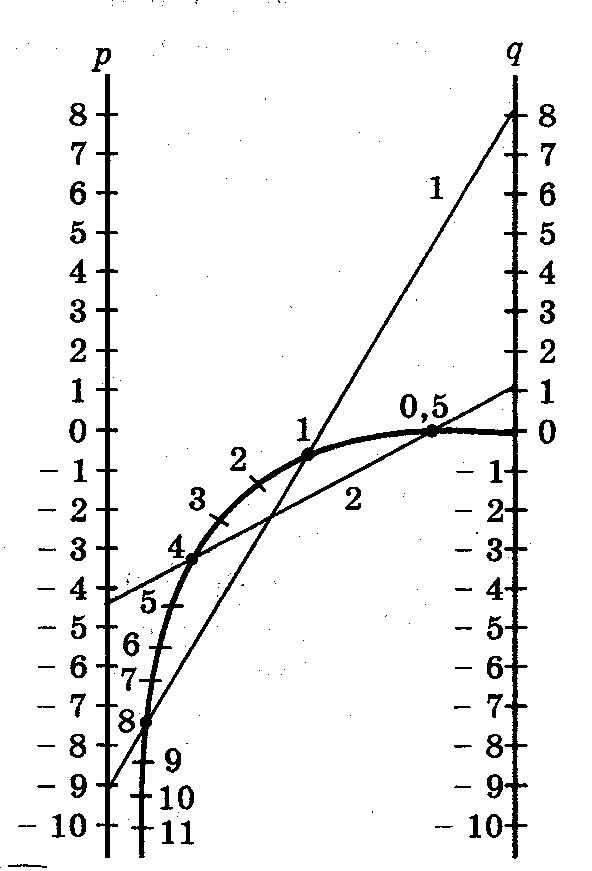
z1 = 8,0 и z2 = 1,0 (рис.12).
2) Решим с помощью номограммы уравнение 2z2 — 9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение
z2 — 4,5z + 1 = 0. Номограмма дает корни z1 = 4 и z2 = 0,5.
3) Для уравнения z2 — 25z + 66 = 0 коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t, получим уравнение t2 — 5t + 2,64 = 0, которое решаем посредством номограммы и получим t1 = 0,6 и t2 = 4,4, откуда
z1 = 5t1 = 3,0 и z2 = 5t2 = 22,0.
6.Подведение итогов.
Жюри объявляет счет. Итоги КВМ. Награждение участников.
7.Рефлексия.
Что понравилось, что не понравилось.
