Конспект урока по Алгебре «Применение свойств арифметического квадратного корня» 8 класс

Урок математики по теме: «Применение свойств арифметического квадратного корня» (8-й класс)

Аксютченко Жанна Владимировна, учитель математики

Тип урока: отработка (закрепление) новых знаний.

Основные цели:

1. формировать навык внесения множителя под знак корня и вынесения множителя из-под знака корня.

2. тренировать способность к рефлексии собственной деятельности;

3. развитие познавательной активности, интереса к предмету, творческой активности.

4. воспитание точности, корректности, логичности в мышлении.

Оборудование, демонстрационный материал: рабочие тетради, цветные карточки — сигналы, задания для самостоятельной работы обучающего характера, карточки с дополнительными заданиями, карточки, содержащие подробное решение заданий, мультимедийный проектор.

План урока (пишется на плакате или на доске).

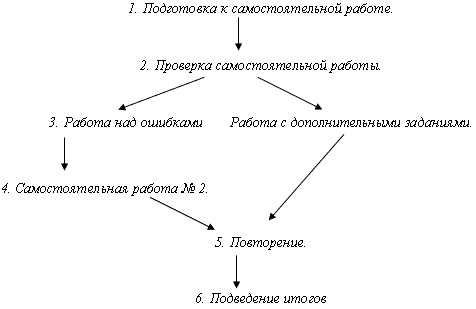
Ход урока.

1. Самоопределение к учебной деятельности

Цель этапа: включить учащихся в учебную деятельность, определить содержательные рамки урока: закрепление приобретенных знаний и умений применять свойства арифметического квадратного корня.

Организация учебного процесса на этапе 1:

– Здравствуйте, ребята!

– Какую тему мы начали изучать на прошлом уроке? (Вынесение множителя из-под знака корня, внесение множителя под знак корня.)

– Сегодня на уроке мы продолжим работать над применением свойств арифметического квадратного корня, а именно будем продолжать формировать навык внесения множителя под знак корня и вынесения множителя из-под знака корня.

2. Актуализация знаний и фиксация затруднений в деятельности

Цель этапа: актуализировать знания в нахождении значений арифметического квадратного корня, в извлечении квадратного корня из степени с четными, нечетными показателями; выполнить самостоятельную работу; зафиксировать задания, вызвавшие затруднение.

Организация учебного процесса на этапе 2:

1. Вычислите:

а)

б)

в)

г)  

2. Вынесите множитель из-под знака корня:

а) ;

б) ;

в) , где а.

3. Внесите множитель под знак корня:

а) 6;

б) -3;

в) а, если а;

г) а, если а.

4. При каких значениях а выражение имеет смысл?

; ; .

Молодцы.

— Сколько корней может иметь квадратное уравнение?

— Как Вы поступите, если понадобится внести отрицательный множитель под знак корня? ( Внесем под знак корня положительный множитель, а знак «минус» оставим перед корнем).

— Как Вы поступите, если потребуется внести переменную под знак арифметического корня?

( рассмотрим два случая: если у0 и у0)

— Сейчас вы будете выполнять самостоятельную работу.

[Учащиеся выполняют самостоятельную работу №1 (5-7 минут)].

Перед проверкой работ:

– Подпишите фамилию и имя вверху таблицы.

– Проверьте задание по образцу и зафиксируйте результат.

По мере проверки учащиеся фиксируют несовпадения с предъявленным образцом и заполняют второй столбец своей таблицы. Если задание выполнено точно так же, как на образце, то в таблице против соответствующего номера они ставятся знак «+», а если есть расхождения, то фиксируют их знаком «?».

3. Выявление причин затруднения и постановка цели деятельности

Цель этапа: указать место в задании, где допущена ошибка, определить правило, в котором допущена ошибка, уточнить цель урока.

Организация учебного процесса на этапе 3:

— Если у вас все ответы и решения совпали, то вам можно приступать к дополнительному заданию.

С теми учащимися, которые допустили ошибки, организовать диалог по локализации затруднения.

— Ну, а те, у кого ответы не совпали Вам надо найти место ошибки и понять её причину.

— Какую цель вы ставите для себя на этом уроке? (Определить причину ошибки и исправить её.)

4. Построение проекта выхода из затруднения. Обобщение причин затруднений во внешней речи

Цели этапа:

• уточнить способы действий, в которых допущены ошибки; исправить ошибки на основе правильного применения правил;

• зафиксировать в речи правила, в которых были допущены ошибки.

Организация учебного процесса на этапе 4:

Учащиеся вместе с учителем выполняют работу с номерами из учебника, учитель на данном этапе выступает в качестве консультанта. Все правила проговариваются во внешней речи.

Физкультурная пауза:

Буратино потянулся,
Раз – нагнулся, два – нагнулся.
Руки в стороны развел,
Ключик видно не нашел.
Чтобы ключик нам достать,
Нужно на носочки встать.

5. Самостоятельная работа с самопроверкой по листу самоконтроля №2

Цель этапа: проверить способность к выполнению заданий, которые на предыдущей самостоятельной работе вызвали затруднение; сопоставить полученное решение с образцом для самопроверки.

Организация учебного процесса на этапе 5:

Выполните вторую самостоятельную работу.

Работа проверяется по листу для самопроверки.

Пока учащиеся выполняют вторую самостоятельную работу, первая группа детей проверяет дополнительные задания по подробному образцу. Результаты фиксируются в таблицу. Если задание выполнено точно так же, как на образце, то в таблице против соответствующего номера они ставятся знак «+», а если есть расхождения, то фиксируют их знаком «?».

6. Включение в систему знаний и повторение.

Цель этапа: тренировать навыки вынесения множителя из-под знака корня, внесения множителя под знак корня.

Организация учебного процесса на этапе 6:

Выбери верный ответ: (у каждого учащегося есть три карточки разного цвета, он поднимает нужного цвета)

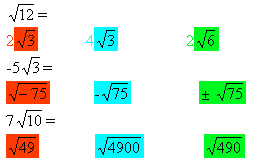
8. Рефлексия деятельности на уроке

Цель этапа: зафиксировать, где были допущены ошибки, способ исправления допущенных ошибок; зафиксировать содержание, которое повторили на уроке, оценить собственную деятельность; записать домашнее задание.

Организация учебного процесса на этапе 8:

– Какую тему мы сегодня повторяли? (применение свойств арифметического квадратного корня.)

– В чём испытали затруднение?

– Над чем необходимо ещё поработать?

– Проанализируйте свою работу на уроке и поставьте себе оценку «5» — всё понимаю; «4» — понимаю, но есть вопросы; «?» — затрудняюсь применять свойства арифметического квадратного корня.

Домашнее задание

Всем: № 413, 417

Задания для выбора:  Построить график у = , Найти О.О.Ф у =

Самоанализ:

Тема урока: Вынесение множителя из-под знака корня, внесение множителя под знак корня.

Данный урок был уроком закрепления знаний и умений. Он тесно связан с предыдущими уроками: квадратный корень из произведения и дроби, квадратный корень из степени, а также с последующими: преобразование выражений, содержащих квадратные корни.

Цели урока

1. формировать навык внесения множителя под знак корня и вынесения множителя из-под знака корня.

2. тренировать способность к рефлексии собственной деятельности;

3. развитие познавательной активности, интереса к предмету, творческой активности.

4. воспитание точности, корректности, логичности в мышлении.

5. добиться сознательного применения учащимися соответствующих алгоритмов для решения типичных упражнений, используя принцип уровневой дифференциации, то есть ребенок, находящийся в зоне ближайшего развития развивается с помощью учителя, а ребенок, находящийся в зоне актуального развития получает возможность на уроке добывать знания самостоятельно и осмысливать их.

Оборудование: рабочие тетради, цветные карточки — сигналы, задания для самостоятельной работы обучающего характера, карточки с дополнительными заданиями, карточки, содержащие подробное решение заданий, мультимедийный проектор.

На этапе актуализации знаний учащихся я предусмотрела различные формы работы, которые способствуют борьбе с перегрузкой учащихся. В предложенных заданиях №1 воспроизводится повторение свойства квадратного корня — квадратный корень из произведения и дроби. Задание №2 нацелено повторить квадратный корень из степени. Задание №3 включает повтор умения решать квадратные уравнения.

Все задания развивают умение анализировать в применении.

Актуализация знаний для всего класса одна и та же.

Затем была проведена самостоятельная диагностическая работа, которая помогла мне определить зоны актуального и ближайшего развития ребенка и тем самым разбить класс на условные группы различного уровня подготовленности. Примеры №1 а и №2 а -оптимальный уровень(различие, воспроизведение); примеры №1б,в и №2 б допустимый(понимание, уровень умений и навыков) пример №2 в- расширенный(уровень переноса, творческий уровень)

Класс работает ограниченное количество времени (5-7 минут). Происходит самопроверка (формирует общеучебные навыки).

Отработка умений и навыков произведена дифференцированно. Для учащихся, находящихся в зоне актуального развития я продумала самоконтроль. На таких уроках он целесообразен, т.к. экономит время, кроме того, учащиеся осознанно подходят к своим “пробелам” и ликвидируют их, не боясь получить низкую оценку. Так же им предложила задания творческого характера. Эти задания предусматривают не только знание предыдущей темы с данной, но и умение совместить их в нестандартной ситуации. Наивысший бал за урок получили ученики, справившиеся со всеми заданиями. Учащиеся, которые недостаточно владеют навыком применения свойств арифметического квадратного корня, работали, получая наибольшую степень помощи от учителя. Далее для этих учащихся опять провожу диагностическую работу, с целью определения удалось ли мне скорректировать знания учащихся по теме » Вынесение множителя из-под знака корня, внесение множителя под знак корня». В это время учащиеся, находящиеся в зоне актуального развития проверяют свое задание по образцу. Важно отметить, что некоторые ученики, справившиеся со 2 диагностической работой, на последующих уроках могут перейти на более высокий уровень развития и имеют реальную возможность получить оценку 4, тем самым, получая возможность испытать учебный успех.

Домашнее задание дифференцированно, что позволяет определить его объем, уровень сложности самостоятельно, по степени усвоения изучаемого материала.

Дифференциация заданий способствует развитию прогрессивного мышления у учащихся с высоким уровнем обучаемости и усвоению обязательного минимума у детей с низким уровнем обучаемости.

Считаю, что поставленные цели были реализованы на уроке, т.к. учащиеся с полным обоснованием выполняли задания на применение свойств арифметического квадратного корня. Так же считаю, что были реализованы обще-учебные умения и навыки (могут найти ошибку и исправить ее, осуществляют контроль над выполняемыми действиями и делают выводы относительно правильности выполнения операций, могут критически осмыслить полученный результат).

На уроке использовались иллюстративные, репродуктивные, частично-поисковые методы и методы самостоятельной работы, репродуктивного и вариативного воспроизведения и применения усвоенных приемов. Положительный, эмоциональный настрой поддерживался на протяжении всего урока; высокая работоспособность обеспечивалась за счет личностно-ориентированного подхода; Считаю, что удалось сформировать умения и навыки как предметные, так и обще-учебные (самоконтроль).

Осуществляя дифференцированный подход к обучению, я придерживалась следующих правил работы:

1. Не сравниваю учеников друг с другом в отношении успехов в учебе.

2. Сравниваю успехи ребенка с самим собой, чтобы он осознавал зоны собственного развития.

3. Поощряю любой успех ребенка.

Структура урока соответствовала его типу. Этапы урока разграничены, по каждому подводился итог. Как показала, проведенная в конце, рефлексия дети получили удовлетворение и радость, они готовы к следующему этапу изучения математики.

Хотелось бы добавить в заключении, что уроки с использованием уровневой дифференциации, в отличие от стандартных позволяют работать каждому ученику в своем темпе.

Приложение (раздаточный материал).

Презентация.