














 Урок на тему:
Урок на тему:
«Прогрессии в окружающем нас мире»
Учитель математики: Дерюгина Ирина Павловна
9 класс
ГБОУ КШ № 1780 г.Москвы
Предмет: алгебра
Класс: 9
Тип урока: комбинированный
Описываемый урок является обучающим и развивающим (нужно научиться использовать прогрессии для решения задач прикладного характера; познакомиться с историей прогрессий, также учащиеся узнают много интересных фактов из жизни)
Цели урока:
обобщить знания по теме “Прогрессии”, повторить все формулы по теме;
показать актуальность темы, ее применение в жизнедеятельности человека;
сформировать навыки применения прогрессии к решению прикладных задач;
продолжить подготовку к итоговой аттестации;
Формирование интереса к изучению математики;
Развитие таких базовых качеств личности, как критическое мышление, рефлексивность, коммуникативность, самостоятельность, толерантность, ответственность за собственный выбор и результаты своей деятельности;
Формирование нового стиля мышления, для которого характерны открытость, гибкость, рефлексивность;
Стимулирование самостоятельной поисковой творческой деятельности.
Задачи урока:
научиться выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий;
закрепить и углубить имеющиеся теоретические знания по теме «Прогрессии»;
Ход урока
1 урок
Организационный момент
Рапорт. Приветствие учащихся и гостей
Актуализация знаний и целеполагание
Учитель: Сегодня мы заканчиваем изучение темы «Последовательности». На предыдущих уроках мы познакомились с разными видами последовательностей, но особое внимание уделили двум последовательностям, каким? (Арифметическая и геометрическая последовательности)
Учитель: Эти последовательности называют…? («Прогрессии»).
Что означает слово «Прогрессия»? (Движение вперед)
Учитель: Сегодня мы будем двигаться вперед, будем повторять, закреплять и систематизировать изученный материал, а также, убедимся, что раздел математики «Прогрессии» является неотъемлемой частью общечеловеческой культуры и окружающего нас мира и ответим на вопрос: «Где же нам могут пригодиться знания о прогрессии?»
Учитель: Для начала, давайте вспомним основные формулы. Для этого заполним таблицу. Я показываю вам карточку с формулой, а вы мне говорите, что она означает (в какую ячейку таблицы стоит ее поместить).(приложение 1)
Учитель: Зная формулы можно решить любую задачу. Давайте проверим. Проведем небольшую разминку.
Устная работа
(На слайде появляются последовательности) Определить, к какому виду последовательностей относится каждая из них:
1; 2; 3;9…
2,4, 8,16,… геометрическая прогрессия, q = 2
1; 11; 21:31;… арифметическая прогрессия d = 10
7;7;7;7; …
1;3;9;16;…
1; 8;27; 125;…
1;3; 9;27; …геометрическая прогрессия, q = 3
2;1;0, 5; 0, 25;… геометрическая прогрессия, q = 0, 5.
Найдите 5 член арифметической прогрессии, если а1=5, d=3. (17)
Найдите 7 член арифметической прогрессии, если а6=20, а8=26. (23)
Найдите 4 член геометрической прогрессии, если b1=-3, q=2. (-24)
Найдите 10 член геометрической прогрессии, если b9=-25,b11=-64. (40)
Найдите сумму натуральных чисел от 1 до 100 (5050)
Обобщение и систематизация знаний. Решение задач
Учитель: Вы молодцы! А теперь приступим к нашей исследовательской работе.
Эпиграфом к нашему уроку я выбрала слова Фридриха Энгельса: « Наука достигает совершенства лишь тогда, когда ей удается пользоваться математикой».
Учитель: Проверим, используются ли формулы прогрессии другими науками, т.е. ответим на вопрос: «Действительно ли прогрессии играют большую роль в повседневной жизни человека?»
В течение урока мы будем заполнять схему, в которой будут отражены области человеческих знаний, где применимы прогрессии. Обратимся к истории вопроса.
ТерещенкоА.: Первые теоретические сведения, связанные с прогрессиями, дошли до нас в документах Древней Греции.
В Древнем Египте в V в до н.э. греки знали прогрессии и их суммы:
1+2+3+…+n = =2+4+6+…+2n = n·(n+1).
Некоторые формулы, относящиеся к прогрессиям, были известны китайским и индийским ученым (V в.)
Примеры отдельных арифметических и геометрических прогрессий можно встретить еще в древневавилонских и греческих надписях, имеющих возраст около четырех тысячелетий и более. В древней Греции еще пять столетий до н.э. были известны такие суммы:
1+2+3+…+n=½n(n+1);
1+3+5+…+(2n-1)=n2;
2+4+6+…+2n=n(n+1).
В клинописных табличках вавилонян, как и в египетских папирусах, относящихся ко второму тысячелетию до нашей эры, встречаются примеры арифметических и геометрических прогрессий.
В трудах АРХИМЕДА излагаются первые сведения о прогрессиях.
Пифагор (IV в. до н. э.) и его ученики рассматривали последовательности, связанные с геометрическими фигурами.
Вопросами последовательности занимался Леонардо Пизанский (Фибоначчи). Наиболее известной из сформулированных Фибоначчи задач является «задача о размножении кроликов», которая привела к открытию числовой последовательности 1, 1, 2, 3, 5, 8, 13, …, именуемой впоследствии «рядом Фибоначчи». Эту задачу мы рассматривали на уроке.
О том, как давно была известна геометрическая прогрессия, свидетельствует знаменитое предание о создании шахмат. Индийский царь Шерам позвал к себе изобретателя шахматной игры, своего подданного Сету, чтобы наградить его за остроумную выдумку. Сета, издеваясь над царем, потребовал за первую клетку шахматной доски 1 зерно, за вторую — 2 зерна, за третью — 4 зерна и т. д. Обрадованный царь посмеялся над Сетой и приказал выдать ему такую «скромную» награду. Стоит ли царю смеяться? На самом деле, нет. Количество зерен равно 18 446 744 073 709 551 615 штук. Если бы царю удалось засеять пшеницей площадь всей поверхности Земли, считая моря, и океаны, и горы, и пустыню, и Арктику с Антарктикой, и получить удовлетворительный урожай, то, пожалуй, лет за 5 он смог бы рассчитаться. Такое количество зерен пшеницы можно собрать лишь с площади в 2000 раз большей поверхности Земли. Это превосходит количество пшеницы, собранной человечеством до настоящего времени.
Учитель: Предлагаю Вам задачу (один человек у доски, остальные в тетрадях).
Задача 1
Из старинного русского учебника математики, носящего пространное заглавие: «Полный курс чистый математики, сочиненный Артиллерии Штык-Юнкером и Математики партикулярным Учителем Ефимом Войтяховским в пользу и употребление юношества и упражняющихся в Математике» (1795г) следующая задачка:
«Служившему воину дано вознаграждение за первую рану 1 копейка, за другую – 2 копейки, за третью – 4 копейки и т.д. По исчислению нашлось, что воин получил всего вознаграждения 655 руб. 35 коп. Спрашивается число его ран».
Решение
Рассмотрим геометрическую прогрессию (bn): 1, 2, 4, :, где b1= 1, g= 2, Sn = 65535
Воспользуемся формулой нахождения суммы n первых членов геометрической прогрессии
![]()
Составим уравнение
![]()
65 535 = 2х — 1
n = 16
При столь великодушной системе вознаграждения воин должен получить 16 ран и остаться при этом в живых, чтобы удостоиться награды в 655 руб. 35 коп.
Ответ: 16 ран
Практическое применение прогрессии – история
Интересный факт
Башкин М. про финансовые пирамиды
Задача 2 (один человек у доски, остальные в тетрадях)
Летом инфузории размножаются бесполым способом делением пополам.
Вопрос: сколько будет инфузорий после 15-го размножения?
Решение
Сколько будет инфузорий после 2-го размножения (4), после 3-го размножения (8), а после 15-го размножения?
Давайте посмотрим последовательность размножения:
1; 2; 4; 8; 16; 32; 64;…
(Это геометрическая прогрессия, первый член которой равен 2 и знаменатель равен 2).
b15=2*2^14= 32768
Ответ: 32768 штук
Учитель: (интересные биологические факты)
1) Способность к размножению у бактерий настолько велика, что если бы они не гибли от разных причин, а беспрерывно размножались, то за трое суток общая масса потомства одной только бактерии могла бы составить 7500 тонн. Таким громадным количеством бактерий можно было бы заполнить около 375 железнодорожных вагонов.
2) Пример Климента Аркадьевича Тимирязева: “Потомство одного одуванчика за 10 лет может покрыть пространство в 15 раз больше суши земного шара”.
3) Пример Карла Линнея: “Потомство пары мух съест мёртвую лошадь также скоро как лев”. Девятое поколение одной пары мух наполнило бы куб, сторона которого равна 140 км, или же составило бы нить, которой можно опоясать земной шар 40 млрд. раз.
4) Всего за пять поколений, то есть за 1 – 1,5 летних месяцев, одна единственная тля может оставить более 300 млн. потомков, а за год её потомство способно будет покрыть поверхность земного шара слоем толщиной почти в 1 метр.
5) Потомство пары птиц величиной с воробья при продолжительности жизни в четыре года может покрыть весь земной шар за 35 лет.
Учащиеся делают вывод о том, что все организмы обладают интенсивностью размножения в геометрической прогрессии.
Практическое применение прогрессии — биология
Задача 3 (один человек у доски, остальные в тетрадях)
Тело, которое свободно падает за 1-ю секунду преодолевает 5 м, а за каждую следующую на 10 м больше, чем в предыдущую. Найти глубину шахты, если свободно падающее тело достигло дна шахты через 5 секунд после начала падения?
Решение
Какой вид прогрессии вы увидели в задаче?
Какие данные мы можем определить по условию?
а1 = 5; d = 10; n = 5
Какой элемент необходимо найти?
an – ? или Sn — ?
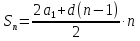

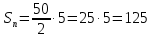
Ответ: 125 метров
Итак, практическое применение прогрессии — Физика
Задача 4 (один человек у доски, остальные в тетрадях)
Представьте, что вы – учетчик на стройке. Привезли и вывезли большое количество бревен строевого леса. Нужно быстро определить, сколько бревен привезли, чтобы закрыть наряд шоферу. Итак, сколько бревен находится в кладке, если в основании 13 бревен?
Решение
В данном случае, чтобы подсчет бревен осуществлялся по простым формулам необходимо использовать факт естественного расположения бревен: в каждом верхнем ряду их оказалось на единицу меньше, чем в нижнем. Тогда число бревен ряда образует арифметическую прогрессию и общее количество легко подчитывается по формуле суммы арифметической прогрессии с d=1 (рис.1)
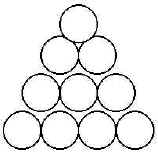
Рис. 1
Sn= =7*13=91 бревно в кладке
=7*13=91 бревно в кладке
Ответ: 91 бревно
Итак, практическое применение — строительство
Перемена
2 урок
Организационный момент
Интересный факт
Мияни Р. о махинациях в Интернете
Задача 5
Курс воздушных ванн начинается с 15 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1ч 45 мин?
Решение
Какой вид прогрессии мы увидели в задаче?
Какие данные мы можем определить из условия?
а1=15, d=10, an=105
Найти n
an=a1+d(n-1)
105=15+10(n-1)
105-15=10n-10
90+10=10n
100=10n
n=10
Ответ: 10 дней
Интересный факт
Мемрук М. о смс-мошенничестве
Задача 6
«Мой дЯдя сАмых чЕстных прАвил…»
Расставьте ударения в приведенном отрывке.
Выпишите номера слогов, на которые падает ударение: 2,4,6,8.
Какая закономерность прослеживается? (это арифметическая прогрессия, а1=2, d=2). Это стихотворный размер с ударением на четных слогах 2; 4; 6;
8;… — Ямб.
«БУря мглОю нЕбо крОет»
Расставьте ударения в приведенном отрывке.
Выпишите номера слогов, на которые падает ударение: 1,3,5,7.
Какая закономерность прослеживается? (это арифметическая прогрессия, а1=1, d=2). Это стихотворный размер с ударением на нечетные слогах стиха — Хорей.
Интересный факт
Юдин А. о сетевом маркетинге.
Учитель: Итак, сегодня на уроке мы с вами решали задачи с помощью арифметической и геометрической прогрессий. Прочитаем еще раз эпиграф нашего урока.
Учитель: В каких же областях научных знаний применима прогрессия? Давайте вернемся к нашей схеме и назовем научные области, в которых решаются задачи с применением формул прогрессий.
История
Биология
Физика
Строительство
Медицина
Литература
Как вам кажется, все ли области мы успели перечислить? (экономика, менеджмент, социология и др.).
Учитель: Также задачи по теме «Прогрессии» нашли широкое применение в заданиях экзамена по математике в формате ГИА. Поэтому в заключение нашего урока я хочу предложить вам выполнить самостоятельную работу, содержащую основные задания по теме «Прогрессии».
Самостоятельная работа
Рядом с каждым заданием – квадратик. Если задание показалось вам легким, и вы без труда справились с ним, поставьте в нем «+», если вы сомневались – «галочку», если вы не знаете, как его решить, оставьте квадратик пустым.
Тест «Последовательности и прогрессии»
Вариант 1
Числовая последовательность задана следующими условиями:
а1 = 2; аn+1 = 3аn – 2. Найдите пятый член этой последовательности.
1) 64 2) 71 3) 81 4) 82
Укажите, какая из нижеперечисленных последовательностей является арифметической прогрессией.
1) 2; 7; 11; 16;… 2) 5; 8; 11; 13;… 3) 7; 9; 10; 12;… 4) 10; 20; 30; 40;…
Найдите номер подчеркнутого члена арифметической прогрессии
(an): 2; 1,9; 1,8; 1,7;…; 0,5;…
Найдите сумму первых пятидесяти членов арифметической прогрессии (an), если известно, что a1=2, a50=147.
Найдите сумму первых ста членов арифметической прогрессии (an), если известно, что a1=–12, d =2.
Найдите неизвестный член геометрической прогрессии
…; 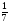 ; х;
; х;  ; …, если
; …, если 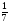 ; х;
; х;  — последовательные члены и х > 0.
— последовательные члены и х > 0.
1) 1 2)  3)
3) 4) другой ответ
4) другой ответ
Сколько положительных членов в последовательности (сn), заданной формулой
Сn = 34 – 4n?
1) 4 2) 8 3) 9 4) 17
Из заданных арифметических прогрессий выберите ту, среди членов которой есть
число –10.
А. аn = 2n + 10 Б. аn = –3n В. аn = –3n + 2 Г. аn = –4n – 8
Тест «Последовательности и прогрессии»
Вариант 2
Числовая последовательность задана следующими условиями:
а1 = 3; аn+1 = 2аn – 10. Найдите четвертый член этой последовательности.
1) 64 2) -49 3) -81 4) 82
Укажите, какая из нижеперечисленных последовательностей является арифметической прогрессией.
1) 5; 8; 11; 13;… 2) 7; 9; 10; 12;… 3) 2; 7; 11; 16;… 4) 10; 20; 30; 40;…
Найдите номер подчеркнутого члена арифметической прогрессии
(an): 2; 1,8; 1,6;…; 0,4;…
Найдите сумму первых сорока членов арифметической прогрессии (an), если известно, что a1=3, a40=138.
Найдите сумму первых пятидесяти членов арифметической прогрессии (an), если известно, что a1=12, d =-2.
Найдите неизвестный член геометрической прогрессии
…; 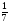 ; х;
; х;  ; …, если
; …, если 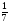 ; х;
; х;  — последовательные члены и х > 0.
— последовательные члены и х > 0.
1) 1 2)  3)
3) 4) другой ответ
4) другой ответ
Сколько положительных членов в последовательности (сn), заданной формулой
Сn = 23 – 4n?
1) 4 2) 8 3) 5 4) 17
Из заданных арифметических прогрессий выберите ту, среди членов которой есть
число –20.
А. аn = 2n + 10 Б. аn = –3n В. аn = –3n + 2 Г. аn = –4n – 8
Итоги урока. Рефлексия. Оценки
— Убедились ли вы, что знания на тему «Прогрессии» важны в человеческой жизни?
— Какие знания вам пригодились сегодня при решении задач?
— Какие задания получались лучше всего?
— Какие трудности испытывали?
— Что понравилось на уроке больше всего?
— Считаете ли вы, что урок был полезен для вас?
— Какими словами можете выразить свое настроение?
Домашнее задание: тест
Домашняя работа «Последовательности и прогрессии»
1. Последовательность задана формулой cn=n²-1. Какое из следующих чисел не является членом этой последовательности?
А. 1 Б. 2 В. 3 Г.4
2. Последовательность задана условиями: c1 = –3, cn + 1 = cn – 1. Найдите с7.
3. Установите соответствие между последовательностью и формулой ее n-го члена.
Последовательность Формула n-го члена
А. Четных чисел 1) an = 7n
Б. Чисел, делящихся на 7 2) bn = (2n – 1)²
В. Квадратов нечетных чисел 3) cn = 2n
4) dn = (7n – 1)²
4. Последовательности заданы несколькими первыми членами. Одна из них — геометрическая прогрессия. Укажите ее.
А. 1/2;1/3;1/4;1/5… Б. 1/2; 1/4;1/8 ;1/16 … В. 1; 4; 7; 10; … Г. 1; 3; 4; 7; …
5. Какая из следующих последовательностей является арифметической прогрессией?
1) последовательность натуральных степеней числа 2
2) последовательность натуральных чисел, кратных 5
3) последовательность кубов натуральных чисел
4) последовательность всех правильных дробей, числитель которых на 1 меньше знаменателя.
6. Из заданных арифметических прогрессий выберите ту, среди членов которой есть
число –10.
А. аn = 2n + 10 Б. аn = –3n В. аn = –3n + 2 Г. аn = –4n – 8
Арифметические прогрессии (хn), (уn) и (zn) заданы формулами n-го члена: xn = 2n – 4, yn = 4n, zn = 4n – 2. Укажите те из них, у которых разность d равна 4.
А. (уn) и (zn) Б. (хn) и (zn) В. (хn), (уn) и (zn) Г. (хn)
8.Фигуры составляются из квадратов, как показано на рисунке. Из какого количества квадратов составлена фигура с номером 100?
|
|
|
|