Разработка урока алгебры в 10-м классе по теме «Решение простейших иррациональных неравенств»
Юргенсон Вероника Александровна, учитель математики
Цель урока: вывести основные приемы решения иррациональных неравенств, продолжать учиться работать в парах, развивать навыки работы с текстом.
Приемы технологии, используемые на уроке: верные и неверные утверждения, таблица, кластер.
Материалы к уроку: на каждого учащегося необходимо распечатать текст из Приложения 1 и карточку с вопросами «Верите ли Вы, что…».
ХОД УРОКА
Стадия вызова (5 минут)
Урок начинает учитель с небольшого вступления.
– Подумаем, что об этом мы уже знаем или предполагаем, что знаем. Создание кластера (используя обозначения ![]() ). Например:
). Например:




– Вдумчиво прочитаем текст.
– Снова вернемся к вопросам, рассмотренным в начале урока, обсудим – правы ли мы были, а если нет, то в чем ошиблись.
– Сформулируем на основании прочитанного текста теоремы, применяемые при решении неравенств.
– Итак, на столах лежат карточки с вопросами. Все вопросы начинаются со слов «Верите ли Вы, что…». Если Вы согласны с утверждением, то справа от вопроса в первом столбце поставьте знак «+», если нет, то знак «–». Работаем в парах. Время работы 5 минут.
Содержание карточки:
| Вопросы | А | Б | В | |
| Верите ли Вы, что … | ||||
| 1. | При умножении обеих частей неравенства на некоторый отличный от нуля множитель, неравенство заменится равносильным. | – |
|
|
| 2. | Возведение обеих частей неравенства в квадрат может привести к потере решений. | + |
|
|
| 3. | Неравенства | – |
|
|
| 4. | Лишние решения в неравенстве можно приобрести не только за счет расширения ОДЗ, но и если не учесть знаки обеих частей неравенства. | + |
|
|
| 5. | Неравенства | – |
|
|
| 6. | Поскольку для любого х из ОДЗ ( | – |
|
|
| 7. | Если возвести неравенство | + |
|
|
| 8. | Для решения неравенства | + |
|
|
После окончания работы учитель предлагает учащимся поделиться своим мнением с классом. (2 минуты). Учитель и ученик на равных позициях, никаких оценок, если учащийся желает, то может прокомментировать.
Заслушав ответы учащихся, учитель заполняет на доске первую строчку таблицы.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Стадия осмысления (10 минут)
Подводя итоги работы с таблицей, учитель приводит учеников к мысли, что, отвечая на вопросы, мы пока не знаем – правы мы или нет. Ответы на вопросы можно получить, прочитав предлагаемый текст из пособия (Приложение 1). Для более вдумчивого чтения, читая текст, на его полях можно расставлять значки: «V» – уже это знал;
«+» – новая информация; «–» – думал иначе, «?» – не понял.
По окончании работы с текстом, каждый у себя в тетради заполняет таблицу:
| «+» | «–» | «?» | |
|
|
|
|
|
И записываем правильное (по мнению учащегося) решение неравенств № 1, 2, 3 из текста.
Закончив работу, пары возвращаются к вопросам, рассмотренным в начале урока, заполняют столбик В и делятся своим мнением с классом. Учитель заполняет вторую строку таблицы на доске.
Но это пока еще не значит, что учащиеся правильно ответили на вопросы.
Стадия рефлексии
Учитель предлагает обсудить полученные результаты (10 минут). Три учащихся на доске записывают решения неравенств. Остальные отвечают на вопросы учителя, возникшие из результатов заполнения таблицы. Например:
– Вы утверждаете, что … утверждение неверное? Обоснуйте.
– Поясните, почему после чтения текста, отвечая на … вопрос, Ваше мнение изменилось? Какое же верное?
– Найдите в тексте утверждение, подтверждающее Ваш ответ на … вопрос.
Рассматриваем предложенные решения, обсуждаем, корректируем.
Обязательно нужно выяснить, не осталось ли каких-либо вопросов по тексту (столбец «?»).
Завершение урока
Самостоятельно попытаться сформулировать и записать в схематичном виде теоремы равносильных переходов, использующихся при решении иррациональных неравенств. Работу выполняем самостоятельно на листочках, листочки сдаем на проверку. (5 минут).
Теоремы.
Неравенство 1. ![]()
Неравенство 2. 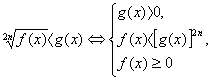
Неравенство 3. 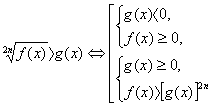 .
.
Приложение 1
Текст для самостоятельного изучения
Решение неравенства не требует практически ничего, кроме умения свести его к решению простейших неравенств, не допустив при этом ни потери, ни приобретения решений. Для этого надо знать свойства функций, изучаемых в школе, и владеть основными понятиями, связанными с равносильностью неравенств. Необходимо иметь в виду, что решение неравенств по сравнению с решением уравнений имеет свои особенности: одни и те же преобразования в применении к уравнениям и неравенствам приводят к разным результатам. Например, при умножении обеих частей уравнения на некоторый отличный от нуля множитель, имеющий смысл в ОДЗ, уравнение заменится равносильным, а для неравенства указанных требований на множитель недостаточно — надо еще требовать, чтобы он был положителен в ОДЗ. Точно так же возведение обеих частей уравнения в квадрат не приводит к потере корней, а то же самое преобразование неравенства может привести и к приобретению, и к потере решений. К сожалению, большинство забывают об этих особенностях.
Как ни удивительно, но большое количество ошибок допускается при решении простейших неравенств. Это происходит, по-видимому, именно из формально понимаемой аналогии между уравнениями и неравенствам. В дальнейшем мы часто будем пользоваться следующим утверждением.
Теорема. Если ![]() и
и ![]() на некотором множестве значений х, то неравенства
на некотором множестве значений х, то неравенства ![]() и
и ![]() равносильны на этом множестве.
равносильны на этом множестве.
Доказательство. Пусть х — произвольное решение первого неравенства из рассматриваемого множества значений х. Если ![]() , то из неравенства
, то из неравенства ![]() на основании теоремы о возведении в степень числовых неравенств, следует неравенство
на основании теоремы о возведении в степень числовых неравенств, следует неравенство ![]() . Если же
. Если же ![]() , то очевидно, что из неравенства f(x) > 0 вытекает, что
, то очевидно, что из неравенства f(x) > 0 вытекает, что ![]() . Тем самым доказано, что всякое решение неравенства
. Тем самым доказано, что всякое решение неравенства ![]() является решением неравенства
является решением неравенства ![]() .
.
Совершенно аналогично доказывается и обратное, что всякое решение неравенства ![]() является решением неравенства
является решением неравенства ![]() . Тем самым теорема доказана. Заметим, что в формулировке теоремы строгие неравенства
. Тем самым теорема доказана. Заметим, что в формулировке теоремы строгие неравенства ![]() и
и ![]() можно заменить на нестрогие:
можно заменить на нестрогие: ![]() и
и ![]() . Доказательство этого факта проводится аналогично.
. Доказательство этого факта проводится аналогично.
При решении неравенств можно приобрести лишние решения, причем они приобретаются как за счет расширения ОДЗ, так и в случае, когда не учтены знаки обеих частей неравенства.
Однако, в отличие от уравнений, при возведении в степень неравенства можно и потерять решения. Учащиеся же, основываясь на неправильно понимаемой аналогии с уравнениями, часто считают, что этого не может быть. Покажем на примерах, как можно приобрести или потерять решения при возведении неравенства в степень. Начнем с примера, в котором можно получить лишние решения за счет расширения ОДЗ.
1. Решить неравенство 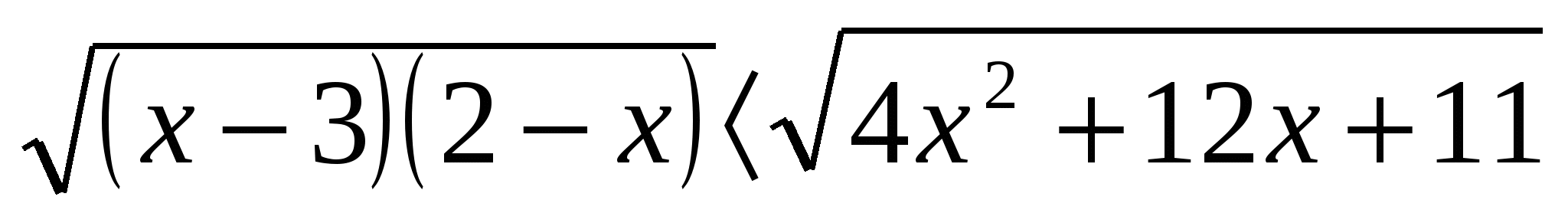 .
.
Некоторые учащиеся дали такое «решение»: «Поскольку правая и левая части этого неравенства неотрицательны, то неравенство можно возвести в квадрат и получить равносильное неравенство ![]() . Квадратный трехчлен в левой части этого неравенства не имеет действительных корней, а потому это неравенство справедливо для всех действительных х. Следовательно, и исходное неравенство справедливо для всех х». Это рассуждение кажется грамотным, однако оно имеет существенный дефект.
. Квадратный трехчлен в левой части этого неравенства не имеет действительных корней, а потому это неравенство справедливо для всех действительных х. Следовательно, и исходное неравенство справедливо для всех х». Это рассуждение кажется грамотным, однако оно имеет существенный дефект.
Оно будет верным лишь в ОДЗ исходного неравенства.
Правильное решение должно быть таким: в ОДЗ обе части исходного неравенства неотрицательны; поэтому в ОДЗ оно равносильно неравенству ![]() , а значит, справедливо для всех х из ОДЗ. Теперь легко найти ОДЗ исходного неравенства, и тем самым получить ответ:
, а значит, справедливо для всех х из ОДЗ. Теперь легко найти ОДЗ исходного неравенства, и тем самым получить ответ:![]() .
.
В следующем примере лишние решения получаются не за счет расширения ОДЗ, а вследствие возведения в степень без исследования знаков обеих частей неравенства.
2. Решить неравенство: ![]() .
.
Вот пример рассуждения, при котором получаются лишние решения: «ОДЗ нашего неравенства: ![]() . Для любого х из ОДЗ справа стоит неотрицательное число, значит, слева стоит положительное число. Поэтому после возведения в квадрат получим равносильное неравенство
. Для любого х из ОДЗ справа стоит неотрицательное число, значит, слева стоит положительное число. Поэтому после возведения в квадрат получим равносильное неравенство ![]() , решения которого х > 1, а также х < —2. Учитывая ОДЗ исходного неравенства, получаем ответ: х > 1,
, решения которого х > 1, а также х < —2. Учитывая ОДЗ исходного неравенства, получаем ответ: х > 1, 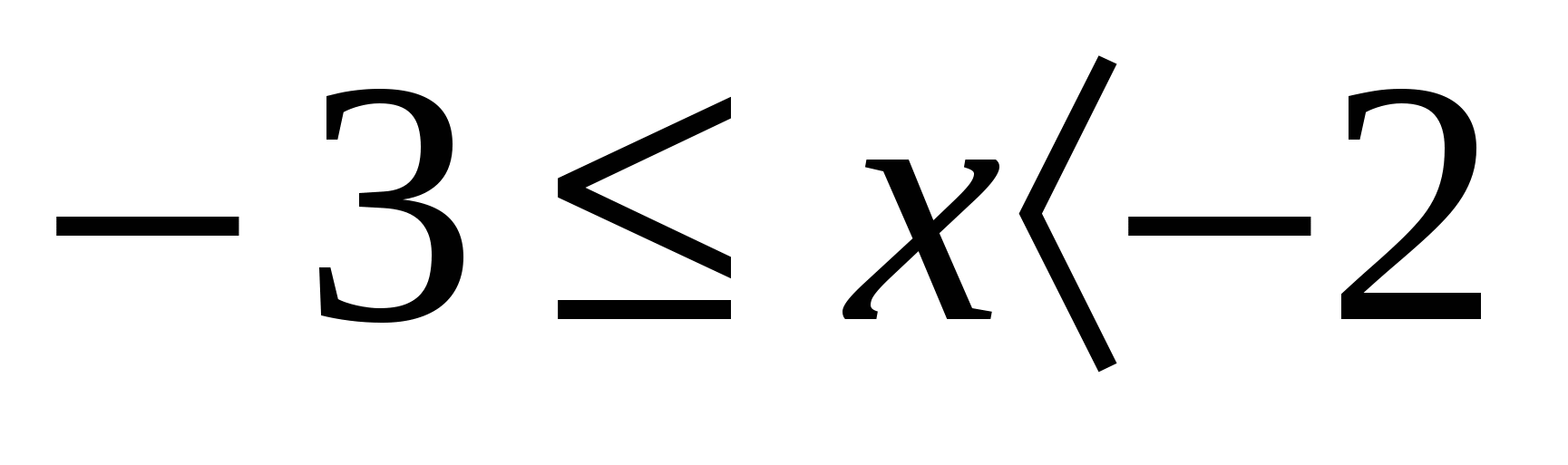 ».
».
На самом деле все х из промежутка 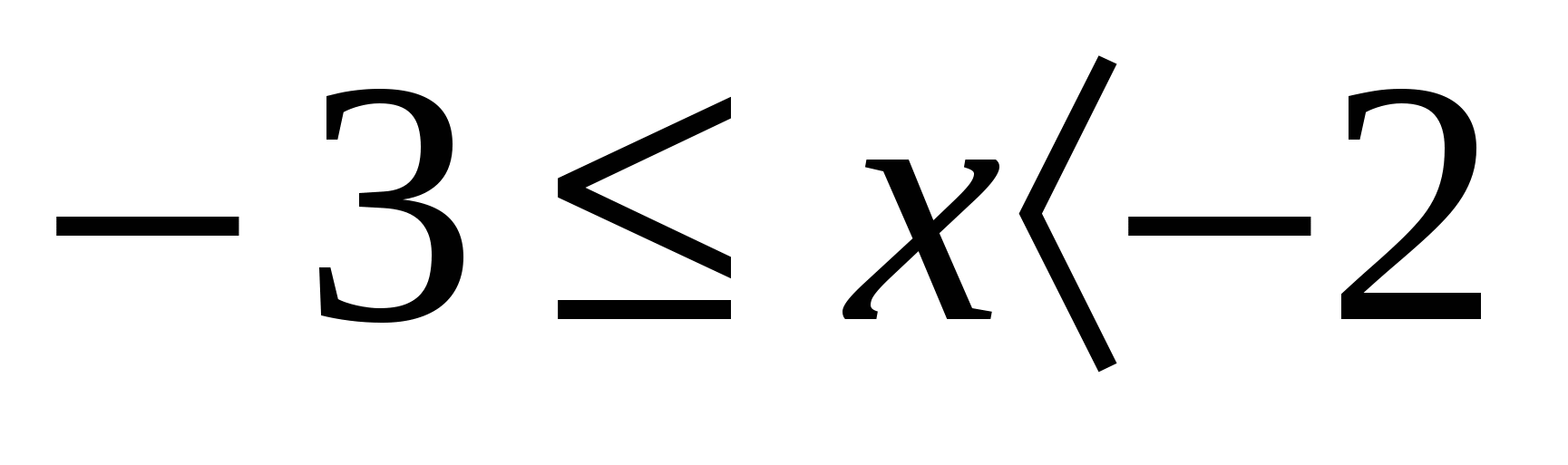 не являются решениями исходного неравенства. Дело в том, что для х из ОДЗ правая часть неравенства действительно неотрицательна, зато левая при некоторых значениях х из ОДЗ — отрицательна. Ясно, что для этих х неравенство не выполняется, т. е. среди них нет решений нашего неравенства. И искать решения исходного неравенства надо среди тех х из ОДЗ, для которых левая часть неравенства неотрицательна, т.е. среди
не являются решениями исходного неравенства. Дело в том, что для х из ОДЗ правая часть неравенства действительно неотрицательна, зато левая при некоторых значениях х из ОДЗ — отрицательна. Ясно, что для этих х неравенство не выполняется, т. е. среди них нет решений нашего неравенства. И искать решения исходного неравенства надо среди тех х из ОДЗ, для которых левая часть неравенства неотрицательна, т.е. среди ![]() . Вот для этих значений х обе части неравенства действительно неотрицательны, его можно возвести в квадрат, получить неравенство
. Вот для этих значений х обе части неравенства действительно неотрицательны, его можно возвести в квадрат, получить неравенство ![]() , которое равносильно исходному на множестве
, которое равносильно исходному на множестве ![]() . Теперь надо из решений неравенства
. Теперь надо из решений неравенства ![]() выбрать те, которые будут удовлетворять условию
выбрать те, которые будут удовлетворять условию ![]() . Они и будут давать решения исходного неравенства.
. Они и будут давать решения исходного неравенства.
Это будут х > 1.
Ошибка в приведенном выше рассуждении состоит в том, что произошла незаметная для учащегося подмена понятий. Действительно, для любого х, являющегося решением исходного неравенства, справа стоит неотрицательное число, а слева положительное число. Однако не все х из ОДЗ будут решениями исходного неравенства, а потому не для всех х из ОДЗ слева будет положительное число. Учащийся слова «для любого х, являющегося решением» заменил словами «для любого х из ОДЗ», и это привело его к ошибке.
3. Решить неравенство ![]() .
.
Если сразу возвести это неравенство в квадрат, то, даже учитывая ОДЗ, мы все равно потеряем решения. Действительно, ОДЗ этого неравенства ![]() . После возведения в квадрат получим неравенство
. После возведения в квадрат получим неравенство ![]() , решением которого будут все х из промежутка —1 < х < 2. Некоторые учащиеся, убедившись, что все полученные х входят в ОДЗ, написали, что это и есть ответ. На самом же деле здесь потеряны решения
, решением которого будут все х из промежутка —1 < х < 2. Некоторые учащиеся, убедившись, что все полученные х входят в ОДЗ, написали, что это и есть ответ. На самом же деле здесь потеряны решения ![]() ; легко убедиться, что для любого числа из этого промежутка левая часть неравенства неотрицательна, а правая — отрицательна.
; легко убедиться, что для любого числа из этого промежутка левая часть неравенства неотрицательна, а правая — отрицательна.
Правильное решение таково.
ОДЗ заданного неравенства состоит из всех ![]() . Левая часть его в ОДЗ неотрицательна, а правая может быть и положительной и отрицательной. Очевидно, что для тех х из ОДЗ, для которых правая часть отрицательна, исходное неравенство будет справедливо. Значит, все х из промежутка
. Левая часть его в ОДЗ неотрицательна, а правая может быть и положительной и отрицательной. Очевидно, что для тех х из ОДЗ, для которых правая часть отрицательна, исходное неравенство будет справедливо. Значит, все х из промежутка 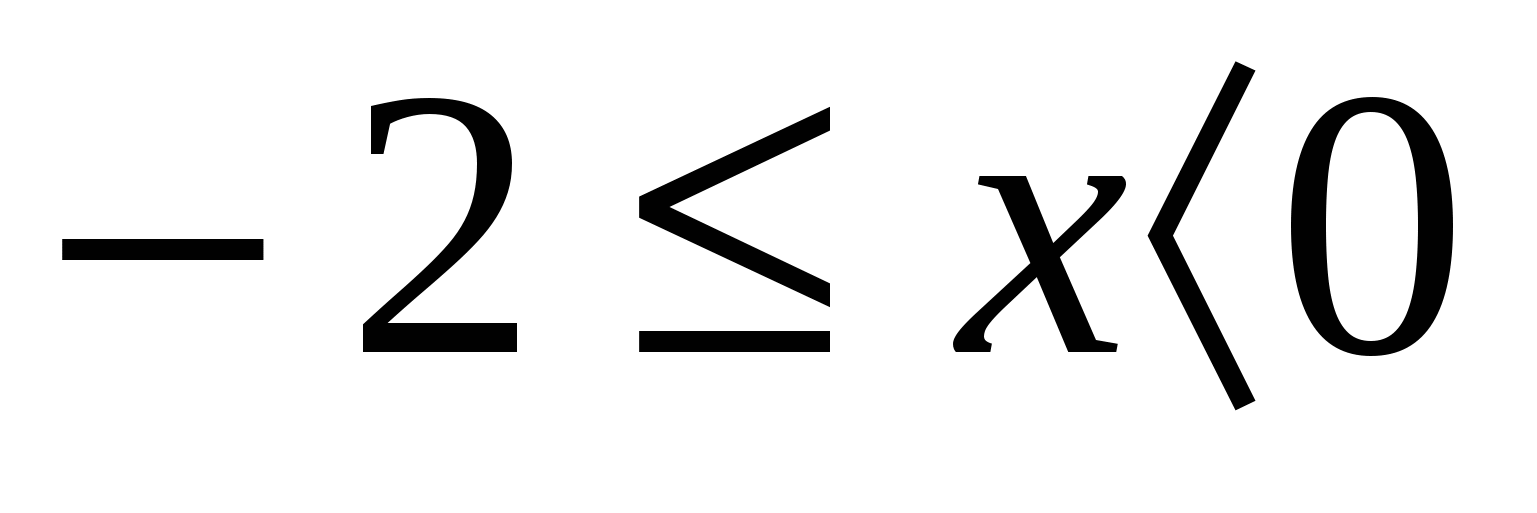 являются решениями исходного неравенства.
являются решениями исходного неравенства.
Рассмотрим теперь значения ![]() . Для всех этих х обе части исходного неравенства неотрицательны, поэтому неравенство можно вознести в квадрат и получить равносильное для всех
. Для всех этих х обе части исходного неравенства неотрицательны, поэтому неравенство можно вознести в квадрат и получить равносильное для всех ![]() неравенство
неравенство ![]() . Решением последнего неравенства будут все х из промежутка
. Решением последнего неравенства будут все х из промежутка
—1 < х < 2. Решением же исходного неравенства в этом случае будут все х из промежутка 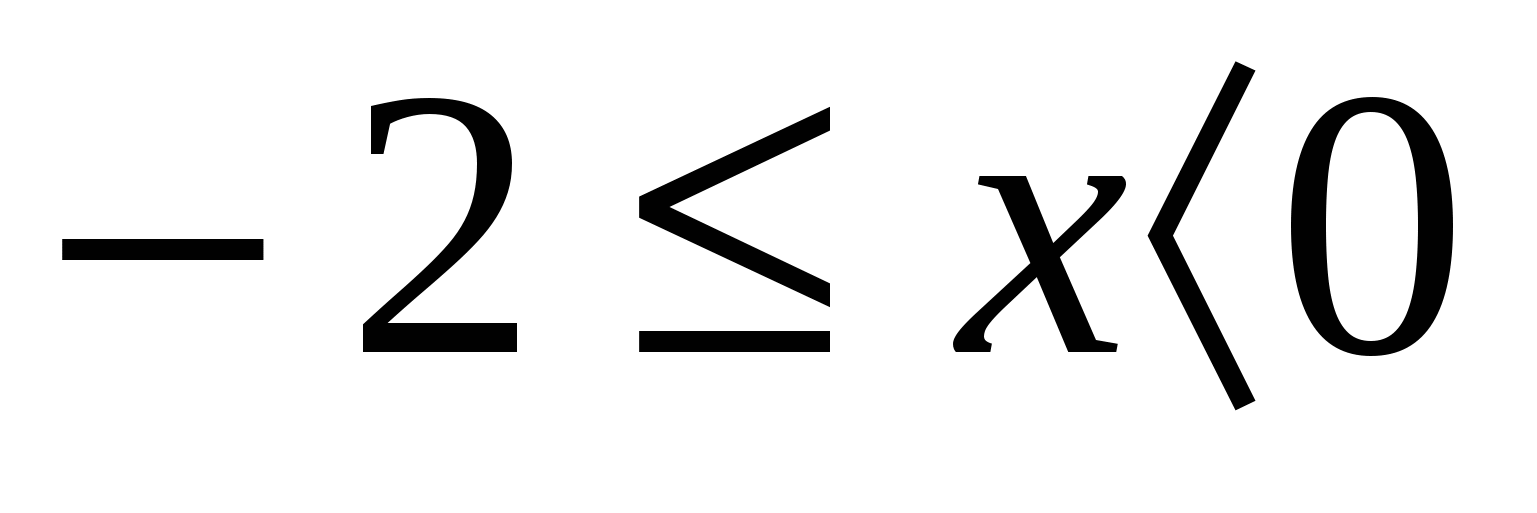 .
.
Объединяя эти два случая, получаем, что решением исходного неравенства будут все значения х из промежутка 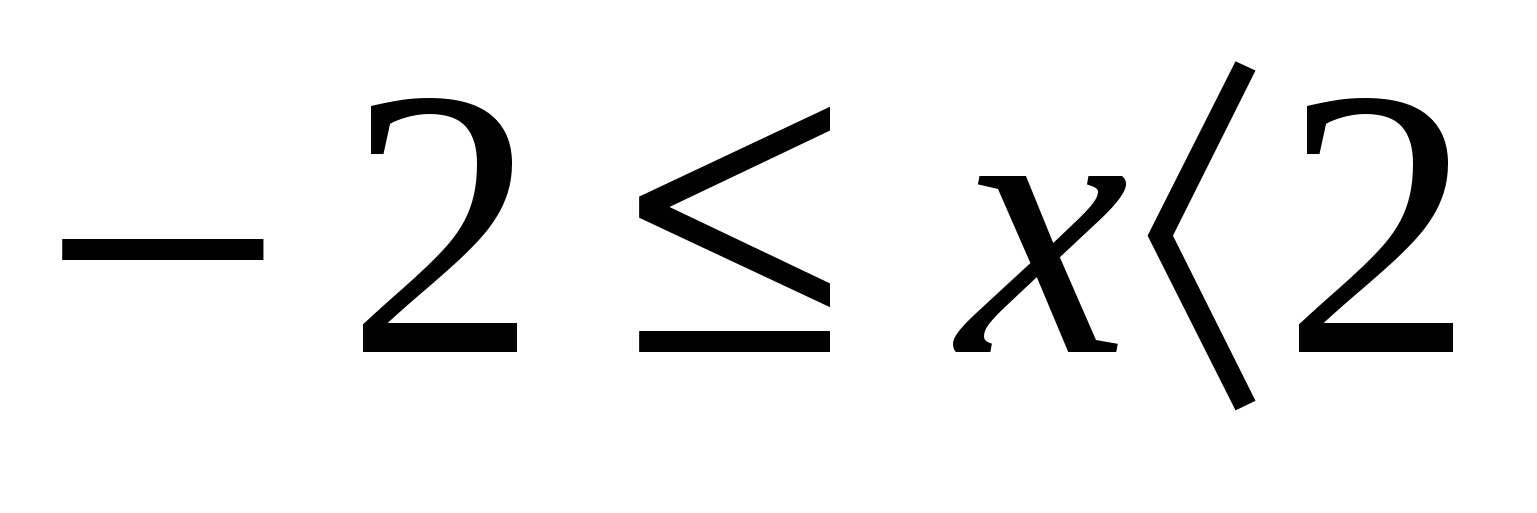 .
.
