Тема урока: «степень с рациональным и действительным показателем».
Цель урока:
-применять свойства степени при выполнении упражнений; знакомство с теоремой, выражающей свойства степени с действительным показателем;
-развить познавательную деятельность учащихся, воспитать интерес к предмету.
Оборудование: проектор.
План урока:
Организационный момент. Постановка целей урока.(2 мин.)
Повторение и закрепление пройденного материала.(15 мин.)
Объяснение нового материала. (10 мин.)
Закрепление нового материала. (10мин.)
Подведение итогов. Домашнее задание. (3мин.)
Ход урока:
I. Организационный момент.
Здравствуйте, садитесь. Тетради с домашним заданием сдаем на проверку.
Сегодня на уроке мы продолжим применять свойства степени при выполнении упражнений. А также познакомимся с теоремой, выражающей свойства степени с действительным показателем.
II. Повторение и закрепление пройденного материала.
С другой стороны доски самостоятельно один человек на оценку:
при каких значениях х выражение имеет смысл?
а) 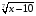
б) 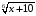
в) 
г) 
Ответы: а) 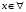 , б)
, б) 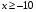 , в)
, в) 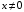 , г)
, г)  .
.
В это время остальные работают устно (примеры высвечиваются на проекторе).
Представить в виде степени с рациональным показателем:
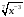 Ответ:
Ответ: 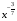
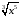 Ответ:
Ответ: 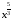
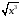 Ответ:
Ответ: 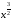
 Ответ:
Ответ: 
Представить в виде корня из степени с целым показателем:
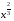 Ответ:
Ответ: 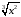
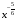 Ответ:
Ответ: 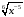
 Ответ:
Ответ: 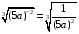
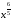 Ответ:
Ответ: 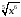
Вычислить:
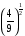 Ответ:
Ответ: 
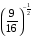 Ответ:
Ответ: 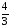
 Ответ:
Ответ: 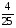
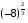 Ответ: не имеет смысла.
Ответ: не имеет смысла.
Проверяем решение с другой стороны доски. Дополнительный вопрос: числа какого вида называются действительными?
Ответ: числа вида 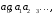 где
где 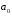 – целое неотрицательное число,
– целое неотрицательное число, 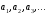 – цифры. (Оцениваем ответ).
– цифры. (Оцениваем ответ).
№57(четные), №58 выполняем устно по цепочке начинаем с третьего ряда. Проговариваем все выполняемые действия.
№57 вычислить. 2) 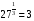 , 4)
, 4) 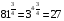 , 6)
, 6) 
№58 вычислить. 1) 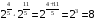 , 2)
, 2) 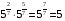 ,
,
3)  , 4)
, 4) 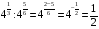 ,
,
5) 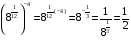 .
.
Записываем число, классная работа.
№59(2,4) у доски один человек на оценку.
Вычислить:
2) 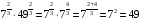 , 4)
, 4) 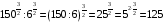 .
.
№62(2,4,6) у доски один человек на оценку.
Представить в виде степени с рациональным показателем:
2) 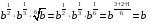
4)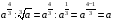
6)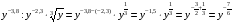
III. Изучение нового материала.
Записываем тему: степень с действительным показателем.
На доске записаны числа: 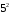 и
и 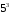 , – сравните их. Очевидно, что
, – сравните их. Очевидно, что 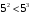 . Сравните следующие пары чисел:
. Сравните следующие пары чисел: 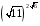 и
и 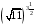 ;
; 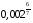 и
и 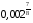 . В этом случае мы не можем определенно сказать какое из чисел больше. Перед нами возникает проблема. Чтобы ее решить, давайте пока отложим эти примеры и запишем следствия, которые нам в этом помогут:
. В этом случае мы не можем определенно сказать какое из чисел больше. Перед нами возникает проблема. Чтобы ее решить, давайте пока отложим эти примеры и запишем следствия, которые нам в этом помогут:
Если  и
и 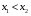 , тогда
, тогда 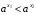 .
.
Если основание больше единицы, то больше то число у которого показатель больше.
Если 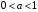 и
и 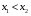 , тогда
, тогда 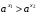 .
.
Если основание меньше единицы и больше нуля, то больше то число у которого показатель меньше.
Если 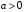 ,
, 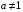 и
и 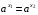 , тогда
, тогда 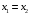 .
.
Если числа 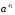 и
и 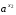 равны, причем основание больше нуля и не равно единице, то показатели равны.
равны, причем основание больше нуля и не равно единице, то показатели равны.
Пусть 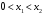 . Тогда
. Тогда
если 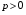 , то
, то 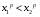 ,
,
если 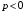 , то
, то 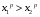 .
.
При возведении неравенства с положительной правой и положительной левой частями в положительную степень знак неравенства не меняется, а при возведении в отрицательную степень знак неравенства меняется на противоположный.
Вернемся к нашим примерам.
Сравните числа: 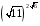 и
и 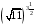 .
.
Воспользуемся теорией:
Сравним основание с единицей.  .
.
Сравним показатели. 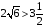 .
.
Так как основание больше единицы, то по первому следствию знак не меняется и  .
.
Ответ:  .
.
Сравните числа: 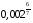 и
и 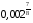 .
.
Воспользуемся теорией:
Сравним основание с единицей. 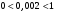 .
.
Сравним показатели.  и
и  .
.  ,
, 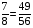 . Значит
. Значит 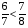 .
.
Так как основание меньше единицы и больше нуля, то по второму следствию знак меняется на противоположный и 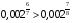 .
.
Ответ: 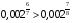 .
.
Закрепление нового материала.
№72(2,4,6) один человек у доски.
Выяснить, какое из чисел больше:
2) 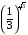 или
или 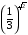 .
.
а) Cравним основание с единицей. 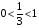
б) Cравним показатели. 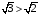 .
.
Так как основание меньше единицы и больше нуля, то по второму следствию знак меняется на противоположный и 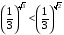 .
.
Ответ: 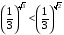
4) 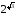 или
или 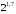 . Проводя аналогичные рассуждения получаем, что
. Проводя аналогичные рассуждения получаем, что 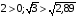 , поэтому
, поэтому 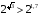 .
.
Ответ: 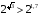 .
.
6)  или
или .
. 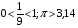 , поэтому
, поэтому 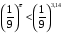 .
.
Ответ: 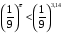 .
.
№75 один человек у доски.
Сравните числа:
1)  и
и 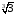 . По свойствам степеней получаем
. По свойствам степеней получаем 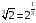 ,
,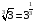 . По IV свойству так как 0<2<3 и
. По IV свойству так как 0<2<3 и 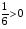 , то знак неравенства не меняется. Т.е.
, то знак неравенства не меняется. Т.е. 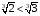 .
.
Ответ: 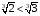 .
.
2)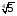 и
и 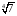 . По свойствам степеней получаем
. По свойствам степеней получаем 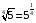 ,
,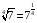 . По IV свойству так как 0<5<7 и
. По IV свойству так как 0<5<7 и 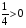 , то знак неравенства не меняется. Т.е.
, то знак неравенства не меняется. Т.е. 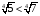 .
.
Ответ: 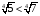 .
.
Записываем домашнее задание: §5, №62(1,3,5), №70(1,3), №72(1,3,5). Спасибо за урок, до свидания!
