Конспект урока по Алгебре «Тригонометрические уравнения»

Захарова Людмила Владимировна
МБОУ «Средняя общеобразовательная школа № 59» г. Барнаула
учитель математики

[email protected]

№1 Простейшие тригонометрические уравнения

Цель: 1. Вывести формулы решений простейших тригонометрических уравнений вида sinx =a, cosx=a, tgx=a, ctgx=a;

2. Научиться решать простейшие тригонометрические уравнения с помощью формул.

Оборудование: 1)Таблицы с графиками тригонометрических функций у=sinx, у=cosx, у=tgx, у=ctgx; 2)Таблица значений обратных тригонометрических функций; 3)Сводная таблица формул для решения простейших тригонометрических уравнений.

План урока-лекции:

1.Вывод формул корней уравнения

а) sinx =a,

б) cosx=a,

в) tgx=a,

г) ctgx=а.

2. Устная фронтальная работа по закреплению полученных формул.

3. Письменная работа по закреплению изученного материала

Ход урока.

В алгебре, геометрии, физике и других предметах мы сталкиваемся с разнообразными задачами, решение которых связано с решением уравнений. Мы изучили свойства тригонометрических функций, поэтому естественно обратиться к уравнениям, в которых неизвестное содержится под знаком функций

Определение: Уравнения вида sinx =a, cosx=a, tgx=a, ctgx=а называются простейшими тригонометрическими уравнениями.

Очень важно научиться решать простейшие тригонометрические уравнения, так как все способы и приемы решения любых тригонометрических уравнений заключается в сведении их к простейшим.

Начнем с того, что выведем формулы, которые «активно» работают при решении тригонометрических уравнений.

1.Уравнения вида sinx =a.

Решим уравнение sinx =a графически. Для этого в одной системе координат построим графики функций у=sinx и у=а.

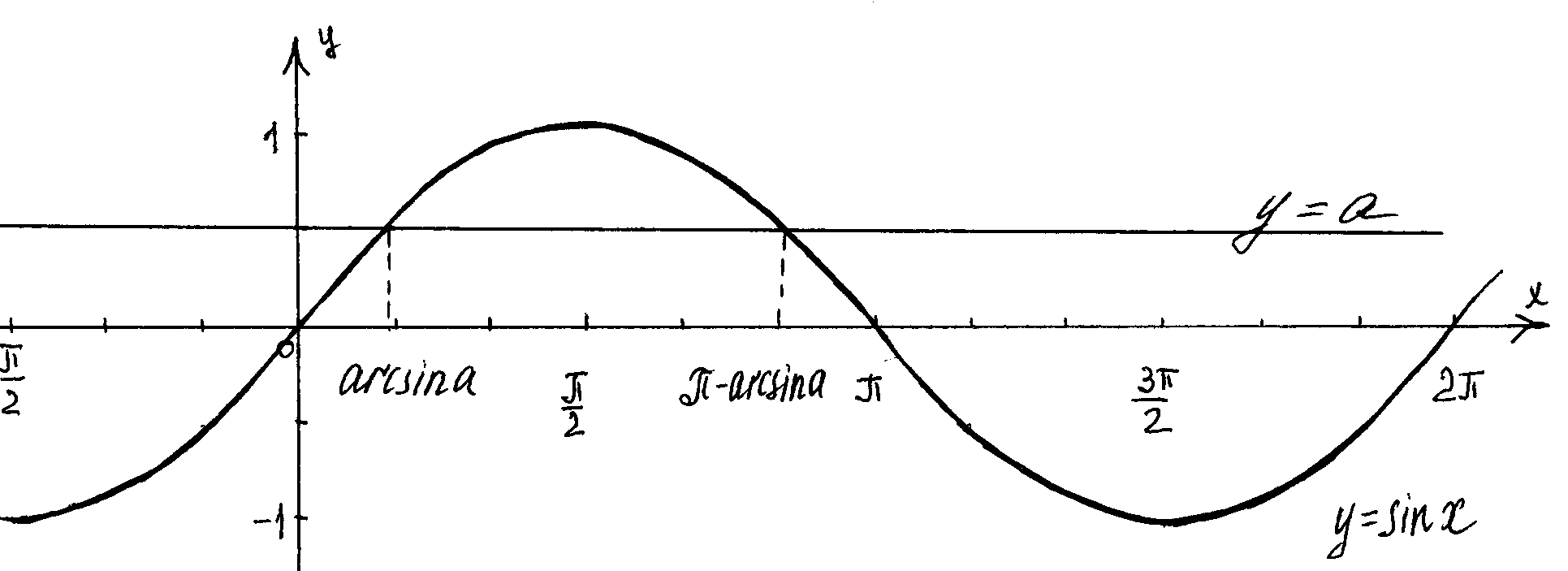
1) Если а> 1 и а< -1, то уравнение sinх=а не имеет решений, так как прямая и синусоида не имеют общих точек.

2) Если -1< а < 1, то по рисунку видно, что прямая у=а пересечет синусоиду бесконечно много раз. Это означает, что уравнение sinx=a имеет бесконечно много решений.

Так как период синуса равен 2, то для решения уравнения sinx=a достаточно найти все решения на любом отрезке длины 2.

Решением уравнения на [-/2; /2] по определению арксинуса х=arcsin a, а на [/2; 3/2] х=—arcsin a. Учитывая периодичность функции у=sinx получим следующие выражения

x=arcsin a+ 2n

х= -arcsin a+2n, n Z.

Обе серии решений можно объединить

х= ( -1)ⁿarcsin a+n, nZ.

В следующих трех случаях предпочитают пользоваться не общей формулой, а более простыми соотношениями:

Если а=-1, то sin x =-1, х=-/2+2n

Если а=1, то sin x =1, x =/2+2n

Если а=0, то sin x =0. x = n,

Пример: Решить уравнение sinx =1/2.

Составим формулы решений x=arcsin 1/2+ 2n

х= —arcsin a+2n

Вычислим значение arcsin1/2. Подставим найденное значение в формулы решений

x=/6+ 2n

х= 5/6+2n

или по общей формуле

х= ( -1)ⁿarcsin 1/2+n,

х= ( -1)ⁿ/6+n,

2. Уравнения вида cosx=a.

Решим уравнение cosx=a также графически, построив графики функций у= cosx и у=а.

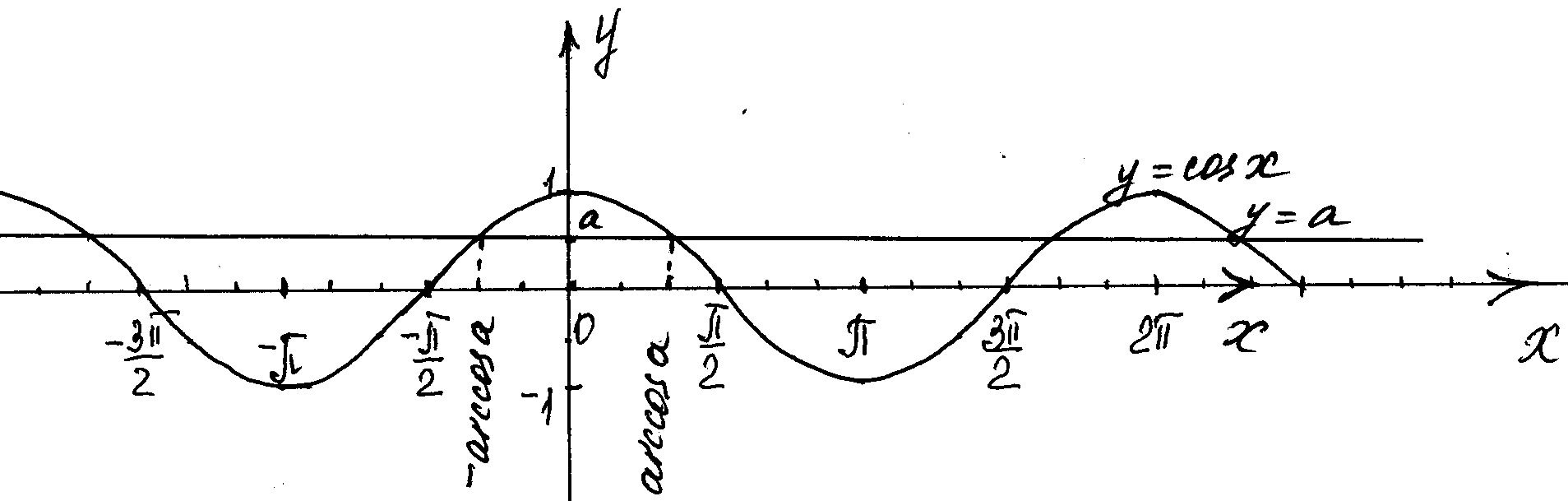
1) Если а<-1