Конспект урока по Алгебре в 11 классе «Способы решения иррациональных уравнений»

Муниципальное общеобразовательное учреждение

Гимназия №10 ЛИК

Города Невинномысска Ставропольского края

Конспект урока по математике
в 11 классе

«Способы решения иррациональных уравнений»

подготовила

учитель математики

Козлова Лариса Викторовна

г. Невинномысск
2013

Цель:

• Систематизировать способы решения иррациональных уравнений.

• Способствовать формированию умения выбирать наиболее рациональные способы решения иррациональных уравнений.

• Закрепить основные методы решения иррациональных уравнений:

— метод возведения обеих частей уравнения в одну и ту же степень;

— метод введения новой переменной.

• Вспомнить нестандартные способы решения иррациональных уравнений.

• Решение заданий части С по материалам ЕГЭ.

Ход урока

1. Этап урока

Изучая тему “Обобщение понятия степени”, мы уже систематизировали и обобщили знания по темам “Корень n-ой степени и его свойства”, “Степень с рациональным показателем”.

А сегодня, наши цели: обобщить знания по теме “Иррациональные уравнения”, повторить способы их решения и научиться выбирать наиболее рациональные для конкретной группы иррациональных уравнений.

Тема эта актуальна, так как иррациональные уравнения часто встречаются на вступительных экзаменах в ВУЗы, с их помощью легко диагностируются знания абитуриентов по многим понятиям, начиная с такого понятия как равносильность уравнений и заканчивая понятием ОДЗ.

Вопросы к классу для фронтального повторения:

1. Какие уравнения называются иррациональными?

Иррациональными называются уравнения, в которых переменная содержится под знаком радикала или переменная возведена в дробную степень.

2. Сформулируйте основной алгоритм решения иррациональных уравнений.

Алгоритм

1. Найти ОДЗ

2. Возвести в одну и ту же степень обе части уравнения

3. Решить полученное уравнение

4. Сделать проверку

3. Назовите известные вам способы решения иррациональных уравнений.

Способы решения иррациональных уравнений

1. Уединение радикала (возведение в одну и ту же степень)

2. Введение новой переменной

3. Умножение на сопряженное выражение

4. Уравнения, содержащие кубические радикалы

5. Уравнения, приводимые к уравнениям с модулями

6. Исследование области определения и области значения

7. Способ равносильных переходов (переход к системе)

2. Этап урока

Широко распространенными иррациональными уравнениями, предлагаемыми на вступительных экзаменах, являются уравнения вида = В(х), где А(х) и В(х) – алгебраические выражения, где неизвестная величина содержится под знаком корня и уравнения вида .

Вернемся к уравнению вида ), тогда

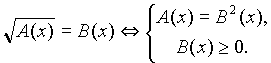
Примеры: (решение выносится на доску)

1) ;

2) = Х.-2

Еще один вид иррационального уравнения сводится к системе

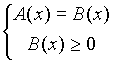
Кстати, можно проверять и А(х) ? 0, т.е. то, что в данной задаче проще. Основные методы решения иррациональных уравнений

1.Поговорим об одном из главных способов решения иррациональных уравнений — способе уединения корня. Итак, рассмотрим первый способ решения иррациональных уравнений и охарактеризуем некоторые его особенности.

А) Решить уравнение: .

В) Решить уравнение:

2. Метод введения вспомогательного неизвестного или “метод замены”.

А) Решить уравнение x² + 3x – 18 + 4 (ЕГЭ 2010 г)

В) Решить уравнение: 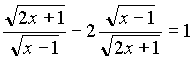( решается на закрытой доске с последующей проверкой)

Часто этот метод встречается при решении других уравнений, не только иррациональных.

3. Уравнения, содержащие кубические радикалы.

Решить уравнение:

(ЕГЭ )

4. “Искусство” или нестандартный подход.

1. Решить уравнение : 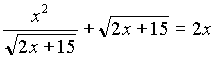(ЕГЭ ).

Разделим обе части уравнения на х >0,

получим уравнение .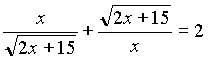

3. Этап урока

Сильным учащимся предлагаются задания:

А)

Решение:

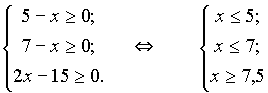
Ответ: нет решения.

В)

По определению левая часть неотрицательное число, а (–1– 2х² < 0), поэтому уравнение не имеет решения.

Остальным учащимся предлагается задание:

Попробуйте догадаться: какими способами можно решить уравнения, записанные на доске?

Самостоятельная работа по группам:

Сгруппировать по 4 методам:

1)

2)

3)

4)

5)

6)

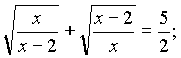
7)

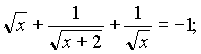
8) .

8) .

Решить уравнения по группам:

• 1 группа: №2, 4;

• 2 группа: №1.

• 3 группа. №3, 5;

• 4 группа. №6, 8.

Защита от каждой группы по одному примеру

Дома: Подобрать и решить из дополнительной литературы 7 примеров, сгруппировав их по методам решения.

Список использованной литературы

1. Алгебра и начала анализа.10-11кл.: Задачник для общеобразовательных учреждений/А.Г.Мордкович

Использованные материалы и Интернет-ресурсы

1. alexlarin.net/ege14.html
2. https://www.edu.ru/