Ф.И.О автора материала: Дыда Татьяна Ивановна
Место работы: МАОУ СОШ № 18, г. Армавир, Краснодарский край
Должность: Учитель математики
Обобщающее повторение в системе
подготовки к ГИА по математике
по теме:
«Арифметическая и геометрическая прогрессии».

Автор – составитель:
Дыда Т. И. – учитель математики
МАОУ СОШ № 18 г. Армавир
§ 1. Числовая последовательность.
Справочный материал.
Если каждому натуральному числу n отнесено по некоторому закону число x, то говорят, что задана числовая последовательность: 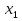 ,
, 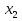 ,
,  , …,
, …,  .
.
Числа 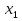 ,
,  называются членами последовательности, они не обязательно различны между собой. В некоторых случаях последовательность задаётся формулой её общего члена
называются членами последовательности, они не обязательно различны между собой. В некоторых случаях последовательность задаётся формулой её общего члена  = f (n), n
= f (n), n 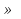 N. Зная её, мы можем получить любой член последовательности. Для этого достаточно в правую часть формулы вместо n подставить номер искомого члена.
N. Зная её, мы можем получить любой член последовательности. Для этого достаточно в правую часть формулы вместо n подставить номер искомого члена.
Например:  =
= 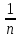 : 1,
: 1, 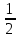 ,
, 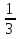 , …,
, …, 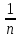 , … ;
, … ;
 =
= : 1; -1; 1; -1; …; 1; … ;
: 1; -1; 1; -1; …; 1; … ;
 = 5 : 5; 5; 5; …; 5; … .
= 5 : 5; 5; 5; …; 5; … .
Последовательность называется возрастающей, если для всех n,  <
<  .
.
Последовательность называется убывающей, если для всех n,  >
>  .
.
Возрастающие и убывающие последовательности называются монотонными.
Например, последовательности монотонные: 1, 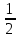 ,
, 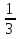 , …,
, …, 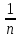 , … ;
, … ;
1, 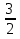 ,
,  , …,
, …,  , …;
, …;
1, 4, 9, …, n², … .
Последовательности не монотонные: 1, — 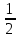 ,
, 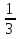 , …,
, …,  ,…;
,…;
1, 0, 3, 0,…, 2n – 1, 0, … .
Замечание. К монотонным последовательностям относятся также неубывающие ( ≤
≤  ) и невозрастающие последовательности (
) и невозрастающие последовательности ( ≥
≥  ).
).
Упражнения.
а) Последовательность ( ) задана формулой
) задана формулой  =
= 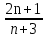 .
.
Найдите  ,
, 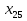 ,
,  ,
,  —
— 
б) Последовательность (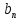 ) задана формулой
) задана формулой 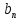 =
= 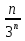 .
.
Найдите 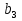 ,
, 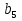 ,
, 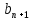 ,
, 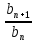 .
.
2. Выпишите первые пять членов последовательности ( ) и задайте эту последовательность формулой n-го члена, если
) и задайте эту последовательность формулой n-го члена, если 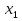 = -10,
= -10,  =
=  + 5, n ≥ 1.
+ 5, n ≥ 1.
3. Для каких членов последовательности ( ) выполняется условие:
) выполняется условие:
а)  > 200, если
> 200, если  = 2n – 5; б)
= 2n – 5; б)  ≤ 30, если
≤ 30, если  = 3n – 100?
= 3n – 100?
4. Составьте одну из возможных формул n — го члена последовательности:
а) 1, 4, 9, 16, 25, … ; в) 0, 3, 8, 15, …; д) 2, 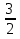 ,
,  ,
,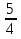 ,… ;
,… ;
б) 2, -2, 2, -2, … ; г) 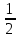 ,
, 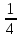 ,
, 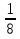 ,
, 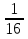 ,… ; е) 5, 0, 5, 0, 5, ….
,… ; е) 5, 0, 5, 0, 5, ….
5. Изобразите последовательность (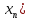 точками координатной прямой:
точками координатной прямой:
а)  =
= 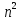 + 1; в)
+ 1; в)  =
= 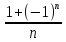 ;
;
б)  = 1 —
= 1 — 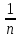 ; г)
; г)  =
=  ·
· 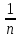 .
.
6. Последовательность (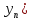 задана формулой
задана формулой  = — 3 ·
= — 3 ·  . Принадлежит ли этой последовательности число: ― 1875?
. Принадлежит ли этой последовательности число: ― 1875?
7. Дана последовательность общий член которой выражается формулой:
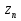 = (4n + 5) (n + 1). Докажите, что последовательность убывающая.
= (4n + 5) (n + 1). Докажите, что последовательность убывающая.
8. Является убывающей или возрастающей последовательность 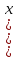 ),
),
если  =
= 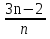 ?
?
9. Последовательность задана формулой  = 2n –
= 2n –  . Какое из следующих чисел является членом этой последовательности?
. Какое из следующих чисел является членом этой последовательности?
1) 2; 2) 4 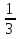 ; 3) 8
; 3) 8 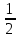 ; 4) 5
; 4) 5 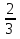 .
.
10. Последовательность задана формулой n-го члена. У какой из них следующий член больше предыдущего?
1)  =
= 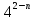 ; 2)
; 2) =
=  ; 3)
; 3)  =
= 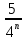 ; 4)
; 4)  = 2 ·
= 2 ·  .
.
11. Последовательность задана формулой 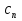 =
= 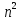 + 1. Какое из чисел является членом этой последовательности?
+ 1. Какое из чисел является членом этой последовательности?
1) 4 ; 2) 6 ; 3) 5 ; 4) 3 .
12. Последовательность задана формулой 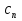 =
= 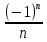 . Какое из этих чисел не является членом этой последовательности?
. Какое из этих чисел не является членом этой последовательности?
1) 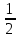 ; 2)
; 2) 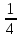 ; 3)
; 3) 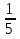 ; 4)
; 4) 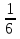 .
.
13. В двух последовательностях, n-е члены которых выражаются формулами  = n(n + 36) +7 и
= n(n + 36) +7 и 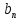 = n(5n + 9), найдите равные члены с одним и тем же номером.
= n(5n + 9), найдите равные члены с одним и тем же номером.
14. Дана последовательность ( ), где n
), где n 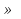 N. Выпишите 4-6 членов этой последовательности, изобразите их точками на координатной прямой и ответьте на вопросы: является ли эта последовательность возрастающей или убывающей, существует ли число, к которому члены последовательности неограниченно приближаются?
N. Выпишите 4-6 членов этой последовательности, изобразите их точками на координатной прямой и ответьте на вопросы: является ли эта последовательность возрастающей или убывающей, существует ли число, к которому члены последовательности неограниченно приближаются?
1)  = -2n; 4)
= -2n; 4)  = 5n; 7)
= 5n; 7)  =
=  ;
;
2)  =
=  · n; 5)
· n; 5)  =
=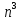 ; 8)
; 8)  = 4 +
= 4 + 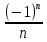 ;
;
3)  =
= 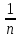 ; 6)
; 6)  =
=  +
+ 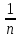 ; 9)
; 9)  = -2
= -2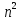 + 3.
+ 3.
15. В последовательность  =
=  найдите расстояние от точки 2 до точки:
найдите расстояние от точки 2 до точки: 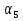 ;
;  ;
;  .
.
§ 2. Арифметическая прогрессия.
Справочный материал.
Числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену, сложенному с одним и тем же число, называется арифметической прогрессией.
Обозначается — ( ):
):  ,
, 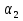 ,
, 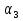 , …,
, …,  , … .
, … .
Разность между любым членом прогрессии и ему предшествующим равна одному и тому же числу, то есть 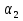 —
—  =
= 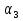 —
— 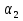 = … =
= … = 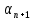 —
—  = … . Это число называют разностью арифметической прогрессии и обозначают
= … . Это число называют разностью арифметической прогрессии и обозначают
буквой d.
Для того чтобы задать арифметическую прогрессию ( ), достаточно знать её первый член
), достаточно знать её первый член  и разность d.
и разность d.
Приведём примеры арифметических прогрессий:
-1; 5; 11; 17; 23; 29; …; здесь  = -1, d = 5 – (-1) =11 — 5 = 17 – 11 = 6;
= -1, d = 5 – (-1) =11 — 5 = 17 – 11 = 6;
17; 14; 11; 8; 5; 2; -1; — 4; …; здесь  = 17, d = 14 – 17 = 11 – 14 = -3;
= 17, d = 14 – 17 = 11 – 14 = -3;
8; 8; 8; 8; 8; 8; …; здесь  = 8, d = 8 – 8 = 0.
= 8, d = 8 – 8 = 0.
Если d > 0, то прогрессия возрастающая;
если d < 0, то прогрессия убывающая;
если d = 0, то прогрессия постоянная последовательность.
Последовательность ( ) является арифметической прогрессией тогда и только тогда, когда её любой член, начиная со второго, является средним арифметическим предшествующего и последующего членов,
) является арифметической прогрессией тогда и только тогда, когда её любой член, начиная со второго, является средним арифметическим предшествующего и последующего членов,
то есть: 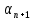 =
=  , где n
, где n 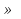 N.
N.
Формулы n-го члена арифметической прогрессии имеют вид:
 =
= 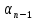 + d и
+ d и  =
=  + d(n – 1) — основные формулы.
+ d(n – 1) — основные формулы.
Формулы суммы n первых членов арифметической прогрессии имеют вид:
 =
=  · n и
· n и  =
= 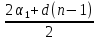 · n
· n
Сумма членов, равноудалённых от концов прогрессии, есть величина постоянная, то есть  +
+  =
= 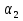 +
+ 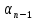 = … .
= … .
Упражнения с решениями.
Задача 1. Найти пятнадцатый член арифметической прогрессии
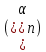 : 3; 7; 11; … .
: 3; 7; 11; … .
Решение.
В прогрессии ( ):
):  = 3,
= 3, 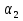 = 7,
= 7, 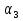 = 11, n = 15.
= 11, n = 15.
Разность арифметической прогрессии d = 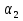 —
—  ; d = 7 — 3 = 4.
; d = 7 — 3 = 4.
По формуле  =
=  + d(n – 1),
+ d(n – 1), 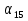 =
=  + 14d = 3 + 4 · 14 = 59.
+ 14d = 3 + 4 · 14 = 59.
Ответ: 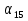 = 59.
= 59.
Задача 2. В арифметической прогрессии ( ) известно, что
) известно, что  = 3, d = 4. Найдите
= 3, d = 4. Найдите  .
.
Решение.
По формуле  =
= 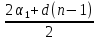 · n , имеем
· n , имеем  =
= 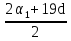 · 20 =
· 20 =  · 20 = 820.
· 20 = 820.
Ответ:  = 820.
= 820.
Задача 3. Между числами 17 и 32 вставить пять таких чисел, чтобы они вместе с данными числами составили арифметическую прогрессию.
Решение.
Имеем прогрессию: 17; 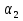 ;
; 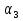 ;
;  ;
; 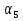 ;
; 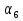 ; 32, значит
; 32, значит  = 17,
= 17,  = 32. Задача сводится к определению разности прогрессии по формуле
= 32. Задача сводится к определению разности прогрессии по формуле
 =
=  + d(n – 1),
+ d(n – 1),  =
=  + d · 6; 32 = 17 + 6d; d = (32 – 17) : 6 = 2,5.
+ d · 6; 32 = 17 + 6d; d = (32 – 17) : 6 = 2,5.

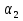 =
=  + d = 17 + 2,5 = 19,5;
+ d = 17 + 2,5 = 19,5;
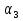 =
=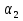 + d = 19,5 + 2,5 = 22;
+ d = 19,5 + 2,5 = 22; 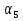 =
=  + d = 24,5 + 2,5 = 27;
+ d = 24,5 + 2,5 = 27;
 =
= 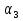 + d = 22 + 2,5 = 24,5;
+ d = 22 + 2,5 = 24,5; 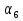 =
= 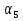 + d = 27 + 2,5 = 29,5.
+ d = 27 + 2,5 = 29,5.
Запишем прогрессию: 17; 19,5; 22; 24,5; 27; 29,5; 32.
Ответ: 17; 19,5; 22; 24,5; 27; 29,5; 32.
Задача 4. Разность арифметической прогрессии равна 4, сумма первых семи членов равна 105. Найти первый и седьмой члены прогрессии.
Решение.
Известно, что 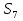 = 105, d = 4.
= 105, d = 4.
По формуле  =
=  + d(n – 1),
+ d(n – 1),  =
=  + 4 · 6;
+ 4 · 6;  —
—  = 24.
= 24.
По формуле  =
=  · n , 105 =
· n , 105 =  · 7;
· 7;  +
+  = 30.
= 30.
Составим и решим систему уравнений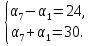
Сложим почленно оба равенства, получим 2 = 54,
= 54,  = 27, тогда
= 27, тогда  = 27 – 24 = 3.
= 27 – 24 = 3.
Ответ:  = 3,
= 3,  = 27.
= 27.
Задача 5. Найдите первый положительный член арифметической прогрессии -10,2; -9,5; …
Решение.
Итак,  = -10,2;
= -10,2; 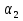 = -9,5. Тогда d =
= -9,5. Тогда d = 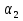 —
—  = -9,5 – (-10,2) = 0,7.
= -9,5 – (-10,2) = 0,7.
По формуле  =
=  + d(n – 1),
+ d(n – 1),  = -10,2 + 0,7 (n – 1),
= -10,2 + 0,7 (n – 1),
 = -10,2 + 0,7n – 0,7 = 0,7n – 10,9.
= -10,2 + 0,7n – 0,7 = 0,7n – 10,9.
По условию  > 0, тогда 0,7n – 10,9 > 0, 0,7n > 10,9; n > 15
> 0, тогда 0,7n – 10,9 > 0, 0,7n > 10,9; n > 15 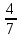 .
.
Но n 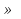 N и <im
N и <im
