












МОУ ЮЛОВСКАЯ ОСНОВНАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА
ИНЗЕНСКОГО РАЙОНА УЛЬЯНОВСКОЙ ОБЛАСТИ
УРОК- ЛЕКЦИЯ
ПО АЛГЕБРЕ
( 9 КЛАСС)
ПО ТЕМЕ:
« ГЕОМЕТРИЧЕСКАЯ
ПРОГРЕССИЯ».
ВЫПОЛНИЛА
УЧИТЕЛЬНИЦА
МАТЕМАТИКИ
Н.И. ЗУБКОВА.
УРОК – ЛЕКЦИЯ
ПО АЛГЕБРЕ ( 9 класс )
ПО ТЕМЕ: «ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ»
( 2 УРОКА)
ЦЕЛЬ УРОКА:
1.Расширить знания учащихся о последовательностях, о прогрессиях.
Ввести понятие геометрической прогрессии, рассмотреть свойства ее членов. С доказательством ввести формулу _п-го члена прогрессии, формулы суммы п первых членов прогрессии. Ввести понятие бесконечной убывающей геометрической прогрессии и формулу суммы ее членов.
2. Способствовать формированию у учащихся логического мышления; вычислительных навыков; внимания и аккуратности при применении определения и формул п-го члена и суммы п первых членов геометрической прогрессии; самостоятельности. Вызвать интерес у учащихся к математике.
3. Способствовать формированию у учащихся умений выделять из представленных последовательностей геометрическую прогрессию, уметь выполнять вывод и применять при решении задач формулы п-го члена и формул суммы п членов геометрической прогрессии.
ПЛАН УРОКА:
Организационный момент.
Постановка цели урока перед учащимися.
Изучение нового материала и его закрепление.
3.1.Определение геометрической прогрессии
3.2.Вывод формулы п-го члена геометрической прогрессии.
3.3.Вывод формулы суммы n— первых членов геометрической прогрессии.
3.4. Определение бесконечной геометрической прогрессии.
3.5. Вывод формулы суммы бесконечной геометрической прогрессии
при | g|<1.
3.6. Сообщение ученика.
4. Подведение итогов урока.
5. Домашнее задание.
6. Литература.
ХОД УРОКА.
1.Организационный момент.
2.Постановка цели урока перед учащимися.
Научиться выделять среди всех последовательностей
геометрическую прогрессию и ее свойства, решать задачи по теме.
3.Изучение нового материала и его закрепление.
3.1.ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ.
ЗАДАЧА.
В благоприятных условиях бактерии размножаются так, что на протяжении первой минуты одна из них делится на две. Запишите колонию, рожденную одной бактерией за семь минут.(см. рисунок).
.
. .
. . . .
. . . . . . . .
1). Выпишите последовательность в соответствии с условием задачи.
1;2;4;8;16;32;64.
или (bп) — последовательность,
b1 =1; b2=2; b3=4; b4=8; b5=16; b6 =32; b7 =64;
2) Найдите частное от деления последующего члена на предыдущий член.
b3 : b2 =4 : 2=2 ;
b4 : b3 =8 : 4=2;
b5 : b4 = 16 : 8=2; и т.д.
g -знаменатель прогрессии.
 = b2:b1= b3:b2=b4:b3=…= bп+1: b п
= b2:b1= b3:b2=b4:b3=…= bп+1: b п
3).Задайте эту последовательность с помощью рекуррентной формулы.
b2 = 2b1
b3= 2 b2
b4= 2b3…..
bп+1 =  b п
b п
УЧИТЕЛЬ: Такую последовательность в математике называют геометрической прогрессией.
4) Формулировка определения геометрической прогрессии.
Учащиеся пытаются дать определение геометрической прогрессии, а учитель помогает им.
5) Работа с учебником.
Учащиеся находят правило в учебнике, один из учащихся
читает определение вслух, учитель обращает внимание
учащихся на то, что в определение сказано «члены отличные
от нуля». Как вы думаете почему?
6).Найдите среднее геометрическое чисел 2 и 8; 4и 16; 8и 32;16и 64.
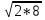 =4
=4
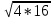 =8
=8
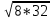 = 16
= 16
 =32
=32
 = bn
= bn
Из равенства  = b2:b1= b3:b2=b4:b3=…= bп: b п-1 = bп+1: b п
= b2:b1= b3:b2=b4:b3=…= bп: b п-1 = bп+1: b п
получим bп: b п-1 = bп+1: b п или b 2п = b п-1 * bп+1 , то
ВЫВОД: Каждый член геометрической прогрессии, начиная со второго, есть среднее геометрическое между предыдущим и последующим членами прогрессии. Отсюда и произошло название прогрессии.
7) Найдите произведение 1 и 7 членов, 2 и 6 членов, 3 и 5 членов геометрической прогрессии и сравните результаты.
b1*b 7 = 1 * 64=64
b2*b 6 = 2 * 32=64
b3*b5 = 4 *16=64
Вывод: b1⋅bп = b2⋅bп-1 = b3⋅bn – 3 = … , т.е. произведение членов, равноудаленных от концов прогрессии, есть величина постоянная.
ЗАДАЧА.1. Дано: ( bn )-геометрическая прогрессия, b1 =3,  =2.
=2.
Найти: первые пять членов прогрессии.
Решение:
b2 = b1* g = 3*2=6
b3 = b2* g =6*2=12
b4 = b3* g =12*2=24
b5 = b4* g =24*2=48
Ответ: 3; 6;12;24;48.
3.2.ВЫВОД ФОРМУЛЫ П-ГО ЧЛЕНА ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ.
( bn)-геометрическая прогрессия , b1 , g.
b2 = b1* g
b3 = b2* g = b1* g* g = b1* g2
b4 = b3* g = b1* g2 * g = b1* g3
b5 = b4* g = b1* g3 * g = b1* g4
…………………………………………….
b n = b1* gn-1
— формула п-го члена геометрической прогрессии.
ЗАДАЧА.2. Дано: ( bn)-геометрическая прогрессия, b1 =8 ,  =
=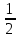 .
.
Найти: , b6
Решение:
b n = b1* gn-1
b 6 = b1* g6-1
b 6 = 8*(  5 = 8*
5 = 8*  =
= 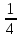 .
.
Ответ: b 6 = 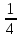 .
.
3.3.ВЫВОД ФОРМУЛЫ СУММЫ n— ПЕРВЫХ ЧЛЕНОВ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ.
ЗАДАЧА-ПРОБЛЕМА 1.
Однажды незнакомец постучал в окно к богатому купцу и предложил такую сделку: « Я буду ежедневно в течение 30 дней приносить тебе по 100 000 рублей. А ты мне в первый день за 100 000 рублей дашь 1копейку, во второй день за 100 000 рублей – 2копейки и так каждый день будешь увеличивать предыдущее число денег в два раза. Если выгодна сделка тебе, то с завтрашнего дня и начнем». Купец обрадовался такой сделке. Он подсчитал, что за 30дней получит от незнакомца 3 000 000 рублей. На следующий день они пошли к нотариусу и узаконили сделку. Кто в этой сделке проиграл?
Учитель: В этой задаче дана последовательность 1,2,4,8,16,32,64,128,256, …,которая является геометрической прогрессией. Надо найти сумму тридцати первых членов этой геометрической прогрессии.
ЗАДАЧА-ПРОБЛЕМА.2.
По преданию, индийский принц Сирам, восхищенный остроумием игры и разнообразием возможных положений шахматных фигур, позвал к себе ее изобретателя ученого Сету и сказал ему: « Я желаю достойно вознаградить тебя за эту прекрасную игру. Я достаточно богат, чтобы исполнить любое твое желание». Сета попросил принца положить на первую клетку шахматной доски 1 пшеничное зерно, на вторую- 2зерна, на третью-4зерна и т. д. Сможет ли принц расплатиться с ученым?
Учитель: В этой задаче дана последовательность 1,2,4,8,16,…, которая является геометрической прогрессией. Надо найти сумму 64-х первых членов этой геометрической прогрессии.
( bn) —геометрическая прогрессия , b1 , g.
Sn — сумма п первых членов геометрической прогрессии
Sn = b1 + b2 + b3 + b4 + b5+… + bn-1 + bn
Sn * g = b1*g + b2*g + b3 *g+ b4 *g + b5 *g+… + bn-1 *g+ bn*g
Sn *g= b2 + b3 + b4 + b5+… + bn + bn *g
Sn *g — Sn = bn *g — b1
Sn (g-1) = bn *g — b1
Sn = 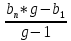
формула суммы п первых членов геометрической прогрессии.
b n = b1* gn-1
Sn = 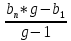
Sn = 
Sn = 
формула суммы п первых членов геометрической прогрессии.
Учитель: Вернемся к предложенным задачам –проблемам .
К задаче 1.
S30 = 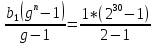 =
= 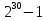 =1073741824 -1 = 1 073 741 823 ( коп)
=1073741824 -1 = 1 073 741 823 ( коп)
К задаче 2.
S64 = 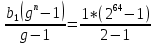 =
=  = 18 446 744 073 709 551 615
= 18 446 744 073 709 551 615  18,5 *1018
18,5 *1018
Если бы принцу удалось засеять пшеницей площадь всей поверхности земли, считая и моря и океаны и горы и пустыни и Арктику и Антарктику и получить удовлетворительный урожай, то за пять лет он бы смог рассчитаться с изобретателем шахмат.
Задача 3 . Дано: ( bn)-геометрическая прогрессия, b1 =8 ,  =
=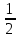 .
.
Найти: S5.
Решение:
Sn = 
S5 = 
S5 = 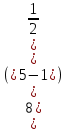 =8* ( —
=8* ( — 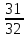 ) * ( —
) * ( —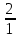 ) =15,5
) =15,5
Ответ: 15,5.
Задача 4 . Дано: 3; — 6; …. — геометрическая прогрессия.
Найти: S6
Решение:
Sn = 
g = b2:b1= -6:3=-2.
S6 = 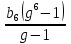
S6 = 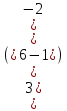 =
=
Ответ: — 63.
3.4.БЕСКОНЕЧНАЯ ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ.
ЗАДАЧА-ПРОБЛЕМА.
Ученик идет от стола учителя к двери. Первый шаг он делает длиной 1 метр, другой — полметра, третий- четверть метра и т.д. Дойдет ли ученик до двери, если до нее 3 метра?
Учитель. Получили последовательность 1,1/2,1/4, 1/8,….Данная последовательность является бесконечной геометрической прогрессией со знаменателем g = 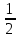 <1.
<1.
Определение: Бесконечно убывающая геометрическая прогрессия — это прогрессия, у которой |q| < 1. Для неё определяется понятие суммы членов бесконечно убывающей геометрической прогрессии как число, к которому неограниченно приближается сумма ![]() первых членов рассматриваемой прогрессии при неограниченном возрастании числа
первых членов рассматриваемой прогрессии при неограниченном возрастании числа ![]() .
.
Найдем сумму всех членов геометрической прогрессии, т.е.
Sn = 1+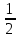 +
+ +
+ 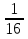 +…..+
+…..+ 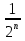
Sn = 
Sn = 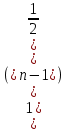 = -2 * ( (
= -2 * ( (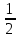 )n -1 ) = 2 —
)n -1 ) = 2 —  2, т.к. при п ∞ вычитаемое стремится к нулю.
2, т.к. при п ∞ вычитаемое стремится к нулю.
Ответ: ученик не сможет дойти до стола учителя.
3.5. ВЫВОД ФОРМУЛЫ СУММЫ БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ | g|<1.
Sn = 
Sn =  =
= 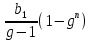
Если | |<1 , то при неограниченном увеличении
|<1 , то при неограниченном увеличении  множитель
множитель 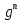 стремится к нулю, а значит разность
стремится к нулю, а значит разность 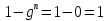 , т.е. стремится к единице. Поэтому при неограниченном увеличении
, т.е. стремится к единице. Поэтому при неограниченном увеличении сумма Sn стремится к числу
сумма Sn стремится к числу .
.
Число  называют суммой бесконечной геометрической прогрессии при
называют суммой бесконечной геометрической прогрессии при
|  |<1.
|<1.
Тогда Sn =  .
.
Заметим, что если |  |>1, то сумма
|>1, то сумма первых членов геометрической прогрессии при неограниченном увеличении
первых членов геометрической прогрессии при неограниченном увеличении не стремится ни к какому числу. Бесконечная геометрическая прогрессия имеет сумму только при |
не стремится ни к какому числу. Бесконечная геометрическая прогрессия имеет сумму только при |  |<1.
|<1.
Задача 5. Дано: 7,(12).
Найти: представить в виде обыкновенной дроби.
Решение:
7,(12)= 7+0,12+0,0012+0,000012+0,00000012+…
0,12; 0,0012; 0,000012… — геометрическая прогрессия
g = b2:b1= 0,0012:0,12=0,01
|g| = 0,01<1.
Sn = 
Sn = 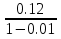 =
= 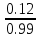 =
= 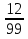
7.(12)= 7+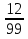 =
=  .
.
Ответ: 7,(12) = 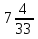 =
=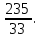
СООБЩЕНИЕ УЧЕНИКА.
Среди геометрических прогрессий особый интерес представляют так называемые бесконечно убывающие геометрические прогрессии.
Рассмотрим квадраты, изображенные на рисунке. Сторона первого
