Урок по алгебре в 9 классе «Задачи с параметрами из сборника»

Задачи с параметрами из сборника

«Алгебра-9 класс, итоговая аттестация (в новой форме)»

(под редакцией Ф.Ф.Лысенко), 2004 г.

Все рассматриваемые задачи расположены в сборнике под № 5 в части 2.

Вариант 1.

Найдите все значения m, при которых окружность x² + y²=10 не имеет общих точек с прямой mx+y=10.

Решение.

Выясним, при каких значениях m окружность и прямая имеют общие точки, решив систему:

х²+у²=10,

у=10- mх;

у =10- mх,

х² + (10-mх)² =10.

Уравнение х² + (10-mх)² -10=0 имеет решение, если D≥0.

х²+100 — 20mх + m²х² -10=0,

(1+m²)х² -20mх+90=0.

= (-10mх)² –(1+m²)90 =100m² -90m² -90 =10(m² — 9)

m² – 9 ≥ 0,

(m-3)(m+3) ≥0,

m є (-∞;-3][3;+∞)

Тогда уравнение, а значит и система, не имеет решений при m є (-3; 3)

ОТВЕТ: m є (-3;3)

Вариант 2.

Найдите все целые значения a, при которых вершина параболы y=2x²+ax+1 лежит «выше» прямой y=x.

Решение:

Пусть (х _в ; у_в) -вершина параболы у=2х²+ах+1, ветви которой направлены вверх.

Вершина параболы будет лежать «выше» прямой у=х, если у_в >х_в.

х_в = ; у_в = = = = (8 — a²)

И

У

У=х

0 х

так,

8—a²)> ,

8- a² > -2a,

a²-2a+8<0,

(a-4)(a+2)<0 , a є (-2 ; 4).

Так как a є Z, то a є {-1;0;1;2;3}

ОТВЕТ: -1; 0; 1; 2; 3.

Вариант 4.

Найдите все значения m, при которых парабола у=х² — х+1 имеет с прямой х + my — 1= 0 одну единственную общую точку.

Решение.

Парабола и прямая имеют единственную общую точку, если система y=x²—x+1,

x+my -1=0 имеет единственное решение.

Выясним, при каких m это возможно:

y=x²-x+1,

x+my-1=0;

x=1-my,

y=(1-my)²-(1-my)+1.

Преобразуем второе уравнение системы:

у=1-2my+m²y² — 1+my+1,

m² y² – (1+m)y+1=0.

Очевидно, что рассматриваемая система имеет единственное решение, если полученное квадратное уравнение имеет единственное решение.

1. Если m=0, то уравнение примет вид: у+1=0, которое имеет единственное решение и условие задачи выполняется.

2. Если m ≠ 0, то квадратное уравнение имеет 1 решение, если его D=0

D = (1+m)²— 4m² = 1+2m+m² — 4m² = 1+2m-3m²,

3m² — 2m -1 = 0,

m =1; m =.

ОТВЕТ: ; 0; 1.

Вариант № 6

При каких a наименьшее значение функции у=х² -2ах+43 на [-2;+∞) равно 7.

Решение:

Ветви параболы у=х² -2ах+43 направлены вверх, значит свое наименьшее значение функция достигает в точке х_в

х_в = = а

По условию х є [-2;+∞), значит возможны 2 случая:

1. Если а ≥ -2, то у_наим=у(а)=а² -2а²+43, что по условию равно 7, т.е. а² -2а²+43=7,

—а² = -36,

а²=36,

а = ±6.

Т.к. а≥ -2, то а=6.

2. Если а<-2, то у_наим=у(-2)=4-2а(-2)+43, что по условию равно 7, т.е.4+4а+43=7,

4а=-40,

А = -10.

ОТВЕТ: -10; 6

Вариант №8.

При каких а число 3 заключено между корнями уравнения х² -2ах+а² -1=0?

Решение:

Ветви параболы у=х² -2ах+а² -1 направлены вверх.

3

Х₁

Х₂

Х

у(3)

Т.к. по условию корни уравнения находятся по разные стороны от числа 3, то нули параболы также находятся по разные стороны от 3. Тогда:

1) уравнение имеет 2 корня, т.е. D > 0;

2) у (3) < 0.

Итак, 4а² -4(а² -1)>0,

9-2а∙3+а² -1<0;

4а² -4а²+4>0,

а² -6а+8<0;

(а-2)(а-4)<0,

а є (2;4).

ОТВЕТ: (2; 4)

Вариант №9

При каких а оба корня уравнения х² -6ах+9а² -2а+2=0 больше 3?

Решение:

Ветви параболы у=х² -6ах+9а² -2а+2 направлены вверх, а нули функции по условию должны быть больше 3. Тогда:

1. Уравнение имеет 2 корня, т.е. D>0;

2. у

   У(3)

   (3)>0.

Итак, 36а² -4(9а² -2а+2)>0,

9-18а+9а² -2а+2>0;

Х₁

Х₂

3

Х

8а-8>0,

9а² -20а+11>0 ;

а>1,

9(а-1)(а-)>0;

а> , т.е. а> .

ОТВЕТ: (1; +∞).

Вариант №10

При каких значениях m вершина параболы у= mx² -7x+4m лежит во второй четверти?

Решение:

Пусть (х_в;у_в) -вершина параболы

х_в = ; у_в =

По условию вершина параболы лежит во II четверти, значит

х_в<0,

у_в>0,т.е. < 0,

>0 ;

m<0,

(4m-7)(4m+7)<0;

m є ( ;0)

ОТВЕТ: (-1,75; 0)

Вариант №11

При каких целых значениях параметра с уравнение + = с имеет хотя бы один корень?

Решение:

Т.к. левая часть уравнения является суммой двух неотрицательных выражений, то и правая часть уравнения — неотрицательное число, т.е. с ≥ 0.

Возведем обе части уравнения в квадрат:

х-2+7-х+2= с²,

5+2= с²,

2 = с ²— 5,

4(7х — х² — 14+2х)= (с² — 5)²,

с² – 5 ≥ 0 ;

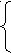28х- 4х² — 56+8х= (с² — 5)²,

(с — )(с + ) ≥ 0;

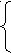— 4х²+36х -56 = (с² — 5)²,

с ≥ ;

х² — 9х + (14 + ) = 0 (*)

D=81- 4∙ (14 + ) =81- 56- (с² -5)² = 25-(с²-5)² = (5- (с²-5))(5+(с² — 5)) = =(10-с²) ∙с²

У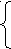равнение (*) имеет хотя бы один корень, если D ≥ 0, значит

с²(10-с²) ≥ 0,

с ≥ ;

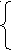(-с)(+с) ≥ 0,

с ≥ ;

—

—

— С

Итак, с є [; ], целые значения: с = 3

ОТВЕТ: с = 3

Вариант № 13

Найдите все значения а, при которых точка пересечения прямых 3х+ау+1=0 и 2х-3у-4=0 находится в третьей координатной четверти.

Решение:

Пусть (х;у)- точка пересечения прямых, причем по условию х<0, у<0.

Найдем координаты точки пересечения прямых из системы:

3х+ау+1=0,

2х-3у-4=0.

х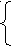=1,5у+2,

3(1,5у+2)+ ау +1=0;

х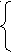=1,5у +2,

(4,5+а)у = -7.

1)Если а = -4,5, то второе уравнение системы не имеет решений, а значит и вся система не имеет решений

2)Если а < -4,5, то 4,5+ а 0, что нарушает условие задачи

3)Если а >-4,5, то 4,5+а > 0, а у < 0 и у = -7/(а+4,5);

у = -7/(4,5+а),

х = 2-10,5/(а+4,5);

у= -7/(4,5+а),

х = (2а+9-10,5)/(а+4,5).

х= (2а-1,5)/(а+4,5).

Т.к. х<0 ,