Хостинг документов » 11 класс » Компьютерное моделирование биотических отношений, 11 класс

Компьютерное моделирование биотических отношений, 11 класс

Муниципальное общеобразовательное учреждение

«Гимназия №32»»

г. Нижнекамск Республика Татарстан

Интегрированный урок биологии и информатики
в 11 классе

Компьютерное моделирование биотических отношений

подготовила

учитель биологии

высшей квалификационной категории

Давлетшина Вероника Васильевна

Цели урока:

1. Формирование умений и навыков, носящих в современных условиях общенаучный и общеинтеллектуальный характер.

2. Развитие у школьников теоретического, творческого мышления, а также формирование операционного мышления, направленного на выбор оптимальных решений, развитие навыков и умений применения современных компьютерных технологий.

3. Формировать у учащихся целесообразность построения компьютерных моделей с целью управления добычей возобновляемых ресурсов.

4. Развитие толерантности, самооценки, самоанализа, умение оценивать работу своих товарищей.

5. Закрепление знания о влиянии на организмы комплекса биотических факторов, взаимодействующих с ними.

6. Использование методов математического компьютерного моделирования для изучения и прогнозирования экологических ситуаций.

Оборудование: мел, доска, компьютеры, мультимедийный проектор.

Программное обеспечение: ОС MS Windows XP, MS Office Excel 2003.

Структура и содержание урока

1. Постановка познавательной задачи урока перед учащимися.

В настоящее время наиболее яркие открытия происходят на стыке наук. Возникают новые науки: биоинженерия, бионика, биоинформатика. Это яркий пример интеграций наук. Сегодня на уроке мы с вами совместим материал биологии и информатики по теме: «Компьютерное моделирование биотических отношений»

2. Повторение изученного материала по биологии

Устный опрос (слайд 2)

1. Что является структурной единицей вида и эволюции? (популяция)

2. Дайте определение понятия «популяции». (это совокупность особей одного вида обитающих на определенной территории, относительно обособленно от других совокупностей того же вида)

3. Приведите примеры популяций.

В природе популяция какого-либо вида играет отведенную ей роль и находится во взаимосвязи с популяциями других видов. В природном сообществе складываются, так называемые биотические отношения. Как внутривидовые, так и межвидовые. Биотические отношения, так или иначе, приводят к изменению численности популяции.

Для понимания функционирования этой единой системы очень важно знать не только особенности биологии тех или иных видов организмов, но и их популяционные характеристики — демографические показатели. (Биомасса, плотность расселения, общая численность, скорость роста численности, продолжительность жизни, рождаемость, смертность, возрастной состав).

Крайне важно знание причин и скорости популяционных изменений, а также умение вести измерения этих природных показателей.

Процессы изменений биологических показателей популяции называются динамикой популяций.

3. Постановка проблемного вопроса: (слайд 3)

По итогам сегодняшнего урока постарайтесь ответить на вопрос: для чего необходимо изучение динамики численности?

В биологии при исследовании развития биосистем строятся динамические модели изменения численности популяций различных живых существ (бактерий, рыб, животных и др.) с учетом различных факторов. Взаимовлияние популяций рассматривается в моделях типа «хищник-жертва».

Прежде чем перейти к моделированию вспомним:

1. Что такое компьютерное моделирование? (моделирование, реализованное средствами программной среды.)

2. Назовите основные этапы построения и исследования компьютерных моделей.

Ответ: (слайд 4)

1 этап. Построение описательной информационной модели.

2 этап. Создание формализованной модели.

3 этап. Построение компьютерной модели.

4 этап. Проведение компьютерного эксперимента.

5 этап. Проведение анализа полученных результатов.

Постановка задачи: (слайд 5)

Этап 1. Постановка задачи или создание описательной информационной модели.

Рассмотрим экологическую систему, содержащую хищника и его жертву (например, жертвы – зайцы, хищники — волки). Будем предполагать, что зайцы питаются растительной пищей, которая имеется в избытке и не ограничивает их размножения, а волки питаются только зайцами.

Свежие документы: Тест по биологии на тему "Дыхательная система человека"

Этап 2. Создание формализованной модели.

При построении математической модели можно исходить их следующих гипотез:

1. Биологические характеристики компонентов неизменны, так же как и взаимоотношения между ними. Система считается однородной в пространстве. Изучаются изменения во времени численности (биомассы) компонентов системы.

2. При сохранении гипотезы однородности вводится предположение о закономерном изменении системы отношений между компонентами. Это может соответствовать либо закономерному изменению внешних условий (например, сезонному), либо заданному характеру эволюций форм, образующих систему. При этом по-прежнему изучается кинетика численности компонентов.

Аппаратом для изучения этих двух классов задач служат системы обыкновенных дифференциальных и дифференциально-разностных уравнений с постоянными (А) и переменными (Б) коэффициентами.

3. Объекты считаются разнородными по своим свойствам и подверженными действию отбора. При решении таких задач используют аппарат теории вероятностей. К ним относятся многие задачи популяционной генетики.

4. Отказ от территориальной однородности и учет зависимости усредненных концентраций от координат. Для описания таких систем необходимо привлечение аппарата дифференциальных уравнений в частных производных. В имитационных моделях часто вместо непрерывного пространственного описания применяют разбиение всей системы на несколько пространственных блоков.

Мы рассмотрим первый класс задач. (слайд 6)

Изучение динамики численности популяций естественно начать с простейшей модели неограниченного роста, в которой численность популяции ежегодно увеличивается на определенный процент. Математическую модель можно записать с помощью рекуррентной формулы, связывающей численность популяции следующего года с численностью популяции текущего года, с использованием коэффициента роста a.

Популяции существуют не изолированно, а во взаимодействии с другими популяциями. Наиболее важным типом такого взаимодействия является взаимодействие между жертвами и хищниками (например, караси-щуки, зайцы-волки, и так далее).

(слайд 7)

В модели «хищник-жертва» количество жертв xn и количество хищников yn связаны между собой.

Коэффициент d показывает рост численности хищников, f — среднее потребление одним хищником жертв ежегодно.

Этап 3. Компьютерное моделирование

Построим в электронных таблицах компьютерную модель, позволяющую исследовать численность популяций с использованием различных моделей: неограниченного роста, и «хищник-жертва».

Задания по группам: (слайд 8)

Цель задания — составить упрощенную математическую модель взаимоотношений хищника и жертвы в сообществе. Начальная численность популяции оленя (жертвы) составляет 2000 особей. Оленями питается волк.. Выжившая к концу каждого года часть популяции оленей увеличивает свою численность на 40%. Начальная численность популяции волков составляет 15 особей, один волк потребляет по 30 оленей ежегодно, годовой прирост популяции волков составляет 10%.

Задача 1

Рассчитайте, какова будет численность оленей через 1, 3, 5 и 10 лет, если начальная численность волков составляет 20 особей и не изменяется на протяжении указанного периода времени.

Отобразите изменения численности оленей в течение данного периода времени графически. Сравните полученный результат с результатом задачи 1.

Решение:

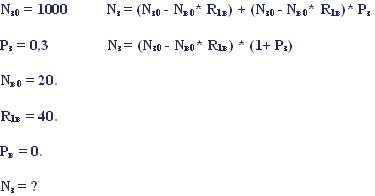
Для популяции волков используем ячейки F 5 – F 15.

Присваиваем F5 = $C$1. Дальше копируем вниз по образцу (популяция волка не меняется по условию).

Для популяции зайцев используем ячейки С5 – С15.

Присваиваем С5 = $C$1.

Формула: С6 = (C5-F5*$D$1)*(1+$B$1). Ячейки С7 – С15 заполняем вниз по образцу.

Свежие документы: Внеклассное мероприятие по биологии в 7 классе «Прогулка под водой»

Задача 2

Рассчитайте, какова будет численность оленей через 1, 3, 5 и 10 лет, если начальная численность волков составляет 20 особей и возрастает на 10% ежегодно.

Отобразите изменения численности оленей в течение данного периода времени графически. Сравните полученный результат с результатами задачи 1 и задачи 2.

Решение:

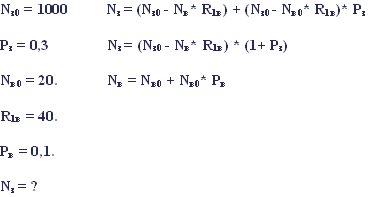
Для популяции волков используем ячейки G5 – G15.

Присваиваем G5 = $C$1. G6 =G5+G5*$E$1.

Для популяции зайцев используем ячейки D5 – D15.

Присваиваем D5 = $A$1.

Формула: D6 =(D5-G5*$D$1)*(1+$B$1). Ячейки D7 – D15 заполняем вниз по образцу.

Задача 3

Рассчитайте, какой должна быть начальная численность растущей популяции волков, чтобы численность оленей была относительно стабильна (т.е. равнялась примерно 2000) в течение первых пяти лет существования популяции.

Решение:

Для популяции волков ячейки H5 – H15.

В задаче требуется подобрать такое начальное количество волков, при котором численность зайцев будет минимально изменяться в течение первых пяти лет существования. Подбирать начальное число будем в ячейке Н1. Поэтому ячейке Н5 присваиваем значение $H$1.

H5 = $H$1. H6 =H5+H5*$E$1.

Для популяции зайцев используем ячейки E5 – E15.

E5 = $A$1.

Формула: E6 =(E5-H5*$D$1)*(1+$B$1). Ячейки E7 – E15 заполняем вниз по образцу.

Изменяя число в ячейке Н1, подбираем значения в ячейках Е5 – Е9 примерно равные 2000.

Такими значениями будут 5 и 6. Наиболее удачное значение – 6 (начальная популяция волков). (слайд 11)

Для проведения компьютерного эксперимента используются опорные карты. Проводится работа в минигруппах. Учащиеся выступают с анализом полученных результатов.

Как будет изменяться численность популяции оленей в течение последующих пяти лет? Представьте все полученные данные графически.

(слайд 9)

Начальная численность популяции зайцев(жертвы) составляет 1000 особей. Зайцами питается волк. Выжившая к концу каждого года часть популяции зайцев увеличивает свою численность на 40%. Начальная численность популяции волков составляет 15 особей, один волк потребляет по 40 зайцев ежегодно, годовой прирост популяции волков составляет 10%.

Задача 1

Рассчитайте, какова будет численность зайцев через 1, 3, 5 и 10 лет при полном отсутствии хищников. Отобразите изменения численности оленей в течение данного периода времени графически. (слайд 10)

Решение:

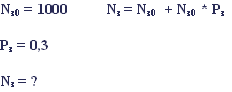Используем ячейки В5 – В15.

Формула для вычислений : В6 = $A$1 =B5+B5*$B$1.

Ячейки В7 – В15 заполняем вниз по образцу.

Задача 2

Рассчитайте, какова будет численность зайцев через 1, 3, 5 и 10 лет, если начальная численность волков составляет 15 особей и не изменяется на протяжении указанного периода времени.

Задача 3

Рассчитайте, какова будет численность зайцев через 1, 3, 5 и 10 лет, если начальная численность волков составляет 15 особей и возрастает на 10% ежегодно.

Задача 4

Рассчитайте, какой должна быть начальная численность растущей популяции волков, чтобы численность зайцев была относительно стабильна (т.е. равнялась примерно 1000) в течение первых пяти лет существования популяции.

Как будет изменяться численность популяции зайцев в течение последующих пяти лет? Представьте все полученные данные графически.

Свежие документы: Урок биологии "Плоские черви" 7 класс

Решение:

Для популяции волков ячейки H5 – H15.

H5 = $H$1. H6 =H5+H5*$E$1.

Для популяции зайцев используем ячейки E5 – E15.

E5 = $A$1.

Формула: E6 =(E5-H5*$D$1)*(1+$B$1). Ячейки E7 – E15 заполняем вниз по образцу.

Изменяя число в ячейке Н1, подбираем значения в ячейках Е5 – Е9 примерно равные 1000.

Такими значениями будут 5 и 6. Наиболее удачное значение – 6 (начальная популяция волков). (слайд 11)

Предполагаемый результат: (диаграмма) (слайд 13)

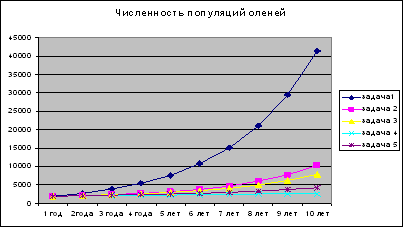
(слайд 12)

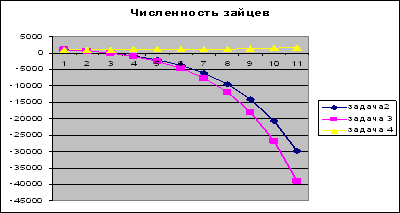
Возможные выводы:

при сравнении трех графиков можно судить о влиянии количества волков на популяцию зайца.

При отсутствии хищников количество особей в популяции стремительно растет ( задача №1), так как рост численности зайцев ничем не сдерживается.

При наличии небольшой популяции волка ( 15 особей) популяция зайца на протяжении двух лет сохраняется на прежнем уровне, а затем исчезает. Здесь играет роль достаточно большое количество волков. 15 волков вполне способны истребить в течение 3 лет популяцию зайца из 1000 особей, несмотря на то, что годовой прирост популяции зайца – 30 %, а годовой прирост популяции волка равен нулю. При годовом приросте численности волков в 10 %, кривая популяции зайцев стремительно падает после 2 лет существования на одном уровне.

Изучение динамики численности играет большую роль в оптимальной эксплуатации природных ресурсов, предсказании вспышек численности вредителей, разработке борьбы с ними. На основе этих исследований решаются вопросы о том, сколько раз в год и в каком количестве можно отстреливать дичь или вести улов рыбы, чтобы получить наибольшую годовую добычу и при этом не нанести вред популяции. Целесообразно ли применять для борьбы с данным видом «вредных насекомых ядохимикаты, и если целесообразно, то в какой сезон и в каком количестве.

Ответы на задачи

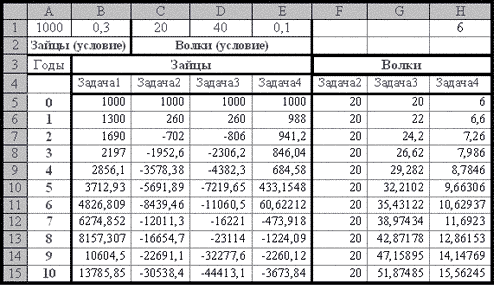
Вывод:

обращение к экологической тематике на уроках информатики позволяет показать детям, как можно применять информационные технологии для решения проблем, связанных с живой природой. Это не только полезно для учащихся, но и делает более интересной работу самого учителя.

4. Итог урока

Математическое и компьютерное моделирование даёт возможность прогнозирования развития популяций. Даёт возможность человеку вносить коррективы в изменение численности популяций, особенно это, актуально применительно к исчезающим видам.

5. Задание на дом (слайд 15)

§ 67, 68 стр. 247, зад. 3,5

В качестве дополнительного задания можно попросить учащихся самостоятельно придумать несколько задач. Это могут быть новые вопросы к уже сформулированным задачам или задачи, основанные на минимальном изменении начальных данных.

6. Оценивание работы учащихся

Приложения

1. Презентация «Компьютерное моделирование биотических отношений»

2. Опорная карта

3. Заготовки для практикума

(Слайд 16)

Литература: