Государственное автономное образовательное учреждение среднего профессионального образования
«Волгоградский техникум железнодорожного транспорта и коммуникаций»
Технический проект
на тему:
«Модель загрязнения воды органическими отходами»
«Производная в биологии»
Выполнила:
Студентка 2 курса
группа 11ОПП
Филимонова В. Р.
Научный руководитель:
Преподаватель математики
Сугак Т.В.
Волгоград
2014
Содержание:
|
| |
|
|
|
| 1 | Введение |
| 2 | Цель и задачи |
| 3 | Этапы работы |
| 4 | Рефлексия |
| 5 | Литература |
|
|
|
|
|
|
Введение.
Озаботившись вопросом экологии, я решила выявить зависимость загрязнения воды от количества поступаемых в нее органических отходов. Этот проект был задуман для наглядного примера того, как люди не берегут природу и загрязняют окружающий себя мир, не задумываясь о том, какой вред это приносит экологии.
Проект направлен на то, чтобы люди задумались о чистоте окружающего мира и о своём здоровье. Расчеты проводились для действующего уровня угрозы загрязнения водной среды. Мне было интересно, а сможет ли водная среда сама себя лечить? При этом от каких параметров водной среды и загрязнения ее органическими отходами зависит очищение воды? Мне было интересно разобраться в этом механизме расчетов, используя математический аппарат в реальной жизни. И так немного пред-истории…
Рассматривается система, состоящая из воды и растворенных в ней кислорода и органических отходов. Концентрация растворенного кислорода и органических отходов связаны между собой. Отходы разлагаются под воздействием бактерий, вызывающих реакцию, которая протекает с потреблением кислорода.
Концентрация отходов может быть измерена так называемой биохимической потребностью кислорода (БПК), которая представляет собой количество кислорода на единицу объёма воды, необходимое для разложения отходов. БПК может измеряться в тех же единицах, что и концентрация кислорода ( например в мг/л).
Обозначим через L(t) концентрацию отходов (БПК) в момент времени t.
Будем предполагать, что скорость разложения отходов пропорциональна их концентрации при условии, что в воде присутствует достаточное количество кислорода для поддержания процесса. Тогда изменение концентрации отходов L(t) описывается уравнением
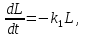 (1)
(1)
где 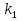 — коэффициент кислорода, 1/день.
— коэффициент кислорода, 1/день.
Обозначим через 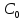 равновесную концентрацию кислорода в воде, которая имеет место при отсутствии отходов, через C(t) — фактическую концентрацию кислорода в воде. Разность
равновесную концентрацию кислорода в воде, которая имеет место при отсутствии отходов, через C(t) — фактическую концентрацию кислорода в воде. Разность 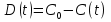
определяет дефицит кислорода в воде. Величина дефицита кислорода D(t) может возрастать во временим t за счёт расхода кислорода на окисление отходов. Однако в природе наблюдается и противоположная тенденция уменьшения дефицита за счёт поглощения кислорода поверхностью воды. Такой процесс называют реаэрацией. Динамика дефицита кислорода описывается уравнением
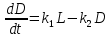 , (2)
, (2)
где 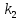 — коэффициент реаэрации, 1/день.
— коэффициент реаэрации, 1/день.
К уравнениям (1) и (2) добавим условие:
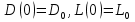 , (3)
, (3)
задающие соответственно дефицит кислорода и концентрацию отходов в начальный момент времени t=0.
Цель и задачи.
Цель:
Целью проекта является вопрос, как с помощью математического аппарата выявить зависимость концентрации загрязнения воды органическими отходами от параметра дефицита кислорода, растворенного в воде.
Задачи:
Построить математическую модель загрязнения воды органическими отходами.
Доказать, что функция дефицита кислорода D(t) определяется следующим образом:
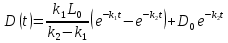
Доказать, что максимальный дефицит кислорода равен:
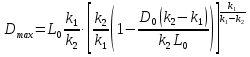
Если установлено, что максимальный дефицит кислорода в воде не должен превышать некоторого заданного уровня 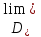 , то как можно найти предельную величину сброса отходов в реку предприятием?
, то как можно найти предельную величину сброса отходов в реку предприятием?
Зная, что течение реки имеет постоянную реаэрации и постоянную потребления кислорода, вычислить какой должна быть максимально допустимая величина БПК в зоне загрязнения, чтобы в любом месте течения дефицит кислорода не превышал заданного уровня, предполагая, что источники загрязнения в верхнем течении реки отсутствуют.
Этапы работы.
Нахождение концентрации отходов L(t)
Докажем, что функция дефицита кислорода D(t) определяется следующим образом:
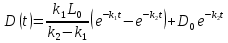
Найдём значение концентрации отходов L(t), исследуя функцию (1).
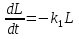
Приводим дифференциальное уравнение к виду с разделяющимися переменными и интегрируем обе части, получаем:
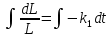
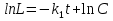 , используя условие (3), что
, используя условие (3), что 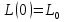 , получим:
, получим:
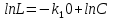
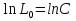
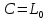
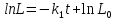
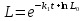
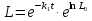
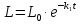 (*)
(*)
Расчёт дефицита кислорода D(t)
Решая дифференциальное уравнение (2), введём подстановку 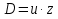 , приведя к ДУ с разделяющимися переменными.
, приведя к ДУ с разделяющимися переменными.
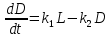
Обозначим: 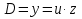 ;
; 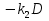 – перенесем в правую часть и вместо L(t) подставим найденное выражение:
– перенесем в правую часть и вместо L(t) подставим найденное выражение: 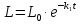 , получим:
, получим:
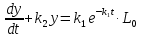
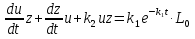
Расчёт вспомогательных функций u и z.
Найдём значения u и z.
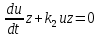 Решая данное уравнение, сократив на z и приведя его к ДУ с разделяющимися переменными, получим:
Решая данное уравнение, сократив на z и приведя его к ДУ с разделяющимися переменными, получим:
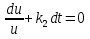
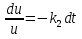 интегрируем обе части, получаем:
интегрируем обе части, получаем:
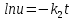
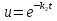
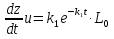 , подставляя в данное уравнение найденное выражение для u, получим:
, подставляя в данное уравнение найденное выражение для u, получим:
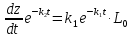
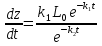
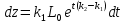 , интегрируем обе части, решая через подстановку, получим:
, интегрируем обе части, решая через подстановку, получим:
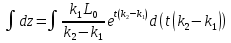
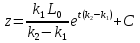
Вычислив u и z, перейдя от у к D(t), получим:
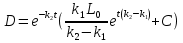
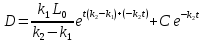
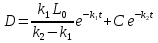 (4)
(4)
Нахождение фактической концентрации кислорода
Для нахождения константы C, подставляем в уравнение (4) начальное условие (3) 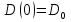 .
.
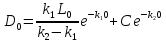
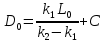
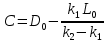
Зная значение константы C, мы можем подставить его в уравнение (4) и найти значение D.
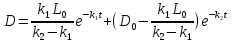
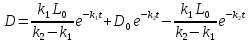
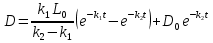 , что и требовалось доказать. (5)
, что и требовалось доказать. (5)
Этой формулой (5) я воспользуюсь для дальнейших расчетов, находя максимальную концентрацию бактерий в воде в момент времени t=0. Для этого вводим обозначение 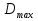 и находим его значение через производную
и находим его значение через производную 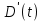 .
.
Докажем что 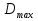 вычисляется по формуле:
вычисляется по формуле:
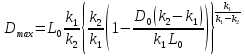
Находим значение производной 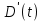 .
.
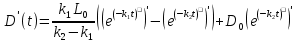
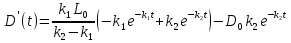
Приравняв производную к нулю, найдем значение 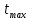
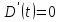
Находим значение 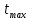 .
.
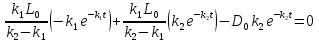
Решаем уравнение относительно неизвестной переменной t.
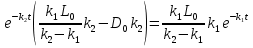
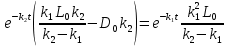
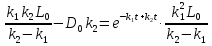
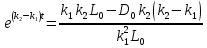
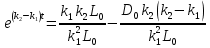
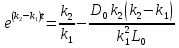
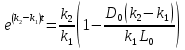
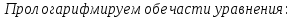
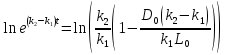
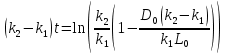
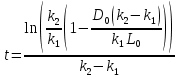
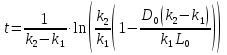
Приравниваем 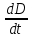 из уравнения (2) к 0 и находим
из уравнения (2) к 0 и находим 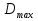 .
.
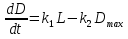
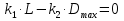
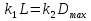 Вместо L подставляем его значение(*), получаем:
Вместо L подставляем его значение(*), получаем:
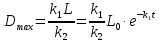 (6)
(6)
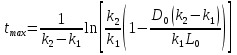 (7)
(7)

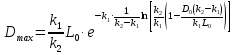
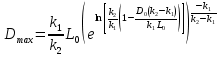
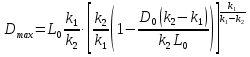 (8)
(8)
Найдем предельную величину сброса отходов в реку предприятием
Предположим, что по течению реки находится промышленное предприятие, которое загрязняет воду отходами, осуществляя их выброс в размере 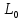 . Попробуем ответить на вопрос: «Если установлено, что максимальный дефицит кислорода в воде не должен превышать некоторого заданного уровня
. Попробуем ответить на вопрос: «Если установлено, что максимальный дефицит кислорода в воде не должен превышать некоторого заданного уровня 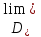 , то как можно найти предельную величину
, то как можно найти предельную величину 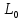 сброса отходов в реку предприятием?» Cледует найти
сброса отходов в реку предприятием?» Cледует найти 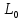 , решая уравнение:
, решая уравнение:
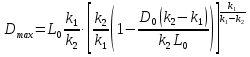
Зная, что источники загрязнения в верхнем течении реки отсутствуют,
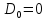 . В результате получаем:
. В результате получаем:
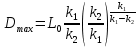
 Выразим из последнего уравнения значение
Выразим из последнего уравнения значение 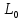 , при этом упростим выражение, содержащее
, при этом упростим выражение, содержащее 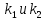 , воспользовавшись свойствами степеней:
, воспользовавшись свойствами степеней:
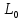 =
=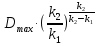 (9)
(9)
Вычислим, какой должна быть максимально допустимая величина БПК в зоне загрязнения?
Решим конкретную задачу, приняв , что течение реки имеет постоянную реаэрации, равную 0,4 1/день, а постоянную потребления кислорода 0,25 1/день. При этом максимально допустимая величина дефицита кислорода в зоне загрязнения в любом месте течения, не превышает 5 мл/л. Предположим, что источники загрязнения в верхнем течении реки отсутствуют. Для ответа на поставленный вопрос воспользуемся формулой (9).
Обозначим за 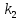 =0,4;
=0,4; 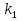 =0,25;
=0,25; 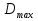 =5;
=5;
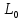 =5
=5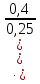
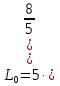 =5
=5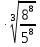 =
=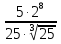 =
=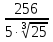 =17,51 (
=17,51 (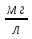 )
)
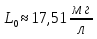
Рефлексия:
Благодаря проведённым исследованиям и расчётам
— удалось построить математическую модель загрязнения воды органическими отходами;
— вывести формулу расчета дефицита кислорода;
— вывести формулу расчета максимального уровня дефицита кислорода в воде;
— зная предельный уровень дефицита кислорода в воде, мне удалось вывести формулу расчета предельного уровня загрязнения органическими отходами;
— и на конкретной задаче были произведены расчеты и найден предельный уровень загрязнения воды органическими отходами;
При этом мне пришлось применить следующий математический аппарат для расчётов:
— умение в данном вопросе использовать и находить производную, решать дифференциальные уравнения с разделяющимися переменными, умение вычислять интегралы, работать со степенями и умение извлекать корни;
Вывод: Полученный результат в реальных цифрах заставляет задуматься: водная среда способна себя реанимировать, если уровень загрязнения в конкретной исследуемой задаче составит 17, 51 мг/л. Это очень малая цифра, я думаю, по сравнению с тем фактом, сколько реально отходов попадает в водную среду. Но это уже новая тема исследования, возможно, моего следующего проекта. Берегите природу, не смотря на то, что она сильная, но и одновременно она и очень хрупкая!!!
Литература
Математические методы в экологии : Сборник задач и упражнений / Е.Е. Семенова, Е.В. Кудрявцева. Петрозаводск: Изд-во ПетрГУ, 2005. 130с.
