Конспект урока по Геометрии «Изучая теорему Пифагора, изучаем её историю»

Конференция по геометрии

по теме «Изучая теорему Пифагора, изучаем её историю»

Цели:

·  Воспитание устойчивого интереса к изучению предмета геометрии, понимания роли геометрии в решении практических задач, возникающих в окружающем нас мире.

·  Воспитание у учащихся общеучебных умений и навыков: работы с дополнительной литературой по математике; поиска, выбора и анализа нужной информации по заданной теме и составления сообщения в краткой форме; оформления наглядности и защиты своего выступления.

·  Расширение знаний учащихся о жизни великого математика Пифагора, о знаменитой теореме Пифагора и ее различных способах доказательства.

Обучать умению говорить перед аудиторией, вести дискуссии, оперировать фактами, обобщать, обоснованно отстаивать свою точку зрения.

Воспитывать культуру речи;

Создать условия, необходимые для развития информационных умений школьников;

Оборудование: компьютер; проектор; экран; для каждой группы таблички.

На доске портрет Пифагора и эпиграф:

 «Геометрия владеет двумя сокровищами: одно из них —
это теорема Пифагора…»
Иоганн Кеплер.

Подготовка к конференции:

Для участия в конференции класс разбивается на группы. Члены групп готовят выступления по теме и наглядные ее представление (презентации)

«Историки» подбирают материалы, которые рассказывают об интересных фактах из жизни Пифагора, о создании пифагорейской школы и основных направлениях математических открытий, сделанных ими.

«Исследователи» занимаются исследованием «троек пифагоровых чисел» и выявляют закономерность их построения.

«Теоретики» изучают предложенную литературу и ищут различные способы доказательства теоремы Пифагора.

«Практики» получают задание найти в литературе практические задачи нетрадиционного содержания, которые решаются с помощью теоремы Пифагора.

«Лирики» занимаются поиском информации о различных названиях теоремы Пифагора и литературные произведения, в которых упоминается теорема.

Ход конференции

• Вступительное слово учителя.

Человечество осмысливает свою жизнь, жизнь предков, ход истории, в том числе развитие науки. Истоки математики находятся в Египте и Вавилонии, но их превращение в полноводный поток проходило в Древней Греции. Первым в ряду философов и математиков древности стоит Пифагор. О жизни Пифагора известно только то, что ничего нельзя утверждать наверняка. О нём написано одновременно и много и мало. Имя Пифагора обросло огромным количеством легенд.

И сегодня мы проводим конференцию по математике, чтобы расширить наши знания о жизни великого математика Пифагора, о его знаменитой теореме, познакомиться с различными способами ее доказательства и показать значение теоремы Пифагора в развитии математики и науки в целом.

Представление группы «Историков» (примерный текст выступления, презентация прилагается)

Биография Пифагора. Родился он около 570 г. до н. э. на острове Самосе в г. Сидоне, расположенном у самых берегов Малой Азии.

Отец Пифагора, Мнесарх, был ювелиром. Он был достаточно богат, чтобы дать сыну хорошее воспитание.

Мать Пифагора звали Пифазис. Это имя она получила от собственного мужа в честь Пифии, жрицы Аполона. Пифия предсказала Мнесарху и его жене появление на свет сына, который превзойдет всех в уме и красоте.

Сын также был назван в честь Пифии. Пифагор — это не имя, а прозвище, которое философ получил за то, что всегда говорил верно и убедительно, как греческий оракул.(Пифагор-«убеждающий речью»).

Пифагор с ранних лет стремится узнать как можно больше. Он обучался в нескольких храмах Греции. По преданию Пифагор, чтобы ознакомиться с мудростью восточых ученых, выехал в Египет и как будто прожил там 22 года. В Египте он создет центр своей философской системы. Пифагор вводит слово «философ»- тот кто пытается узнать. До него ученые называли себя мудрецами – «тот кто знает».

Хорошо овладев всеми науками, в том числе и математикой, он переехал в Вавилон, где прожил 12 лет и ознакомился с научными знаниями вавилонских жрецов.

Затем у халдейских магов изучает теорию чисел. И, может быть, отсюда пошла та числовая мистика приписывания числам божественной силы, которая Пифагором была преподнесена как философия.

После возвращения домой Пифагор попытался создать на родине свою школу, которая вызвала недовольство жителей острова, и Пифагору пришлось покинуть родину. Он переселяется в южную Италию — колонию Греции — и здесь, в Кротоне, вновь основывает школу — пифагорейский союз, просуществовавший почти тридцать лет.

Школа Пифагора. Свою школу Пифагор создает как тайную организацию со строго ограниченным числом учеников из аристократии, и попасть в нее было не просто. Претендент должен был выдержать ряд испытаний; по утверждению некоторых историков, одним из таких испытаний являлся обет пятилетнего молчания, и все это время принятые в школу могли слушать голос учителя лишь из-за занавеса, а увидеть могли только тогда, когда их «души будут очищены музыкой и тайной гармонией чисел».

Пифагорейцы были увлечены построением правильных геометрических фигур с помощью циркуля и линейки. Увлеченные этим «строительством» они выстроили фигуры в плоть до правильного пятиугольника и озадачились тем, как с помощью циркуля и линейки построить правильный семиугольник?(это им не удалось).

Несомненно, со школы Пифагора в математику твердо вошло положение о необходимости строгих доказательств, что и придало ей значение особой науки.

Последние годы жизни Пифагора. Однако судьба самого Пифагора и его школы имела печальный конец, потому что идеология, лежавшая в основе деятельности школы, неуклонно влекла его к гибели. О смерти Пифагора известно мало, существует как минимум 3 версии его ухода:

·  Преследование пифагорейцев

·  Пифагор и пифагорейцы прибыли в Метапонт, где произошла вспышка народного восстания. Он погиб в ночных стычках.

·  В Метапонте — от разрыва сердца.

Пифагор не оставил после себя собрания сочинений, он держал свое учение в тайне и передавал ученикам устно. В результате тайна умерла вместе с ними.

Итак, это тот самый человек, чьим именем была названа теорема, которую все мы учим в школе. Пифагор являлся первым выдающимся ученым, который утверждал, что явления природы можно объяснить математически.

Нам стоит поблагодарить Пифагора за половину всех изобретенных полезных «вещиц».

Учитель. Мы посмотрели и прослушали выступление группы «Историков» о величайшем древнегреческом математике Пифагоре, узнали о его жизни и творчестве, о его школе. А группа «Исследователей» Продолжит нам рассказ о том, чем еще интересовались ученики в школе Пифагора.

Представление группы «Исследователей».

Пифагору приписывается высказывание: «Все есть число». К числам (а он имел в виду лишь натуральные числа) он хотел свести весь мир, и математику в частности. Но в самой школе Пифагора было сделано открытие, нарушавшее эту гармонию. Было доказано, что  не является рациональным числом, т. е. не выражается через натуральные числа.

Пифагорейцы и числа. Пифагорейцы изучили варианты, в которых величины всех сторон прямоугольного треугольника выражаются целыми числами. Вообще, они придавали числам очень большое значение, считая, что через них можно выразить все закономерности в мире. И сами числа они наделяли разнообразными свойствами. Например, они считали, что 5- символизирует цвет, 6- холод, 7- разум, здоровье и свет, 8- любовь и дружбу, и так далее.

Числа, которые изучали Пифагорейцы. Числа, равные сумме всех своих делителей, такие как 6, 28, 496, 8128, они считали совершенными. А пары чисел, в которых каждое число равнялось сумме делителей другого, они называли дружественными.

Пифагорейцы разделили числа на четные и нечетные и заметили, что если складывать последовательно нечетные числа: 1+3+5+7…,то после каждого сложения будут получаться полные числовые квадраты: 1,4,9,16…

Пифагоровы тройки. Пифагоровы числа — тройки целых положительных чисел х, у,z, удовлетворяющих уравнению х2 + у2 =z2 Все решения этого уравнения, а следовательно, и все Пифагоровы числа выражаются формулами х = а2 – b2 , у=2аb, z=а2 + b2 , где а ,b – произвольные целые положительные числа (а> b).

Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам еще около 2300 г. до н. э

По мнению Кантора гарпедонапты, или «натягиватели веревок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.

Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м и привяжем к ней по цветной полоске на расстоянии 3м от одного конца и 4м от другого. Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра.

Не подлежит, однако, сомнению, что эту теорему знали за много лет до Пифагора. Так, за 1500 лет до Пифагора древние египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным, и пользовались этим свойством(т. е. обратной теоремой Пифагора) для построения прямых углов в планировке земельных участков и сооружений зданий.

Да и поныне сельские строители и плотники, закладывая фундамент избы, изготовляя ее детали, вычерчивают этот треугольник, чтобы получить прямой угол.

Учитель. Итак, из сообщения группы «Исследователей», можно сделать вывод, что эта теорема сформулирована за много столетий раньше вавилонскими, китайскими и индийскими учеными, но доказать этот факт они не могли. Вершиной достижений пифагорейцев является доказательство теоремы Пифагора. И сейчас группа «Теоретиков» вам представит некоторые из доказательств этой знаменитой теоремы.

Представление группы «Теоретиков».

№1 Док — во теоремы Пифагора, основанное на построении равнобедренных треугольников

Дано:  АВС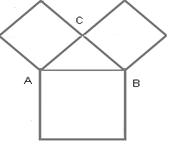

a = b

Угол С = 90

Доказать: с2=а2+b2

Док — во

1)Построим: квадрат со стороной а; квадрат со стороной с;

квадрат со стороной b

2)Построим диагонали квадратов, получим равнобедренные

треугольники, равные треугольнику АВС

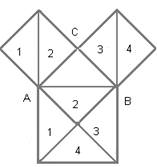3)Площадь квадрата со стороной с складывается из учетверенной площади треугольника АВС, а площадь квадрата со сторонами а и b – из удвоенной площади треугольника АВС:

с2 = 4SABC

а2 = 2SABC

b2 = 2SABC

Следовательно, с2=а2+b2

№2 Док — во теоремы Пифагора, предложенное древними индусами

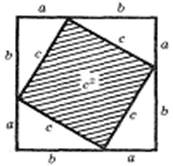
Для первого квадрата:
(a + b)2 = c2 + 4SABC.

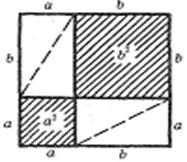
Для второго квадрата:

(a + b)2 = a2 + b2 +4SABC.

Следовательно, c2+4SABC = a2+b2+4SABC.

с2 = a2 + b2

Древние индусы не записывали доказательство, а свои рисунки сопровождали словом «СМОТРИ»

№3 Док — во теоремы Пифагора, основанное на разрезании квадратов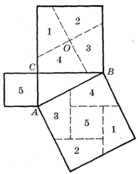

Известны доказательства теоремы Пифагора, основанные на разрезании квадратов, построенных на катетах, на фигуры, из которых можно сложить квадрат, построенный на гипотенузе.

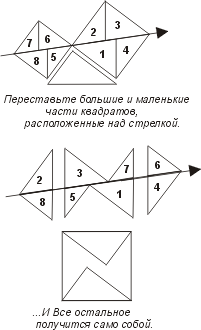
№4 Доказательство Бетхера.

На рисунке дано весьма наглядное разложение Бетхера.

• №5 Доказательство Перигаля.

• В учебниках нередко встречается разложение указанное на рисунке (так называемое «колесо с лопастями»; это доказательство нашел Перигаль). Через центр квадрата, построенного на большем катете, проводим прямые, параллельную и перпендикулярную гипотенузе. Соответствие частей фигуры хорошо видно из чертежа.

С глубокой древности математики находят все новые и новые доказательства теоремы Пифагора, все новые и новые замыслы ее доказательств. Таких доказательств – более или менее строгих, более или менее наглядных – известно более двухсот, но стремление к преумножению их числа сохранилось. ДЕРЗАЙТЕ!

Учитель. Группа «теоретиков» нас познакомила с несколькими доказательствами теоремы Пифагора. Область применения теоремы также достаточно обширна. Не будем пытаться привести все примеры использования теоремы — это вряд ли было бы возможно. Но группа «Практиков» познакомит нас с некоторыми примерами применения этой теоремы.

Представление группы «практиков».

ЗАДАЧИ Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?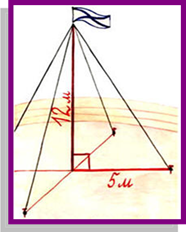

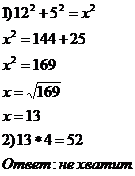Решение

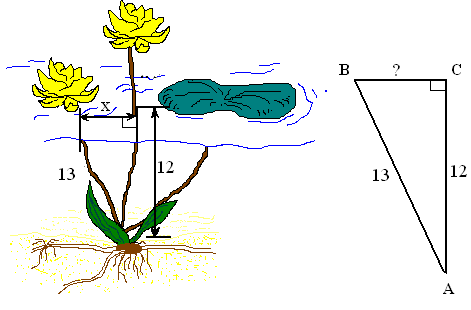
У египтян была известна задача о лотосе:

«На глубине 12 футов растет лотос с 13-футовым стеблем. Определите, на какое расстояние цветок может отклониться от вертикали, проходящей через точку крепления стебля ко дну.»

Попробуйте сами решить эту задачу. Естественно, при решении использовалась теорема Пифагора.

Исторические задачи очень часто представляли в стихах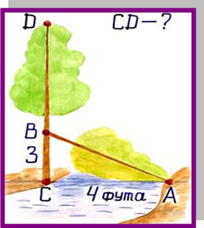

Задача Бхаскари

«На берегу реки рос тополь одинокий. 
Вдруг ветра порыв его ствол надломал. 
Бедный тополь упал. И угол прямой 
С теченьем реки его ствол составлял. 
Запомни теперь, что в этом месте река 
В четыре лишь фута была широка 
Верхушка склонилась у края реки. 
Осталось три фута всего от ствола, 
Прошу тебя, скоро теперь мне скажи: 
У тополя как велика высота?»

Задача о бамбуке из древнекитайского трактата «Гоу-гу»

Имеется бамбук высотой в 1 чжан. Вершину его согнули так, что она касается земли на расстоянии 3 чи от корня (1 чжан = 10 чи).
Какова высота бамбука после сгибания?

Задача из учебника «Арифметика» Леонтия Магницкого

«Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать».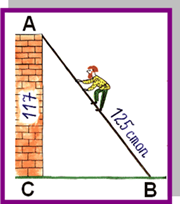

Некоторые области применения теоремы Пифагора:

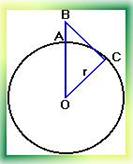
1.Мобильная связь. Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)

Решение:

 Пусть AB= x, BC=R=200 км, OC= r =6380 км.

OB=OA+AB
OB=r + x.

Используя теорему Пифагора, получим 2,3 км.

2.Строительство:

* Окна

* Молниеотводы

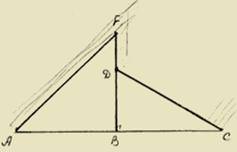
* Крыши. При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки. Например: в доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки AC=8 м., и AB=BF.

 Решение: Треугольник ADC — равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда:

 А) Из треугольника DBC: DB=2,5 м.,

 Б) Из треугольника ABF:  AF= =   5,7

Учитель. Широка область применения теоремы Пифагора. Мы еще неоднократно встретимся с ней на уроках геометрии. Существуют много легенд, мифов, рассказов, песен, притчей, небылиц, анекдотов, частушек об этой теореме. И группа «Лириков» поведает нам о некоторых из них.

Представление группы «лириков».

Многие при имени Пифагора вспоминают его теорему, но мало кто знает, что он имел отношение не только к математике, но и к литературе…

Пифагор- это не только великий математик, но и великий мыслитель своего времени. Вот некоторые его высказывания:

• Мысль — превыше всего между людьми на земле.

• Не садись на хлебную меру (т. е. не живи праздно).

• Уходя, не оглядывайся (т. е. перед смертью не цепляйся за жизнь).

• По торной дороге не ходи (т. е. следуй не мнениям толпы, а мнениям немногих понимающих).

• Ласточек в доме не держи (т. е. не принимай гостей болтливых и не сдержанных на язык).

• Будь с тем, кто ношу взваливает, не будь с тем, кто ношу сваливает (т. е. поощряй людей не к праздности, а к добродетели, к труду).

Одна из самых главных заслуг Пифагора – это теорема, которая носит его имя…

Если дан нам треугольник

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем:

Катеты в квадрат возводим,

Сумму степеней находим-

И таким простым путём

К результату мы придём.

Теорема Пифагора нашла свое отражение и в литературе: в легендах; в стихах и песнях.

Легенда о теореме Пифагора

Сохранилась легенда, которая гласит, что доказав свою знаменитую теорему, Пифагор принес богам в жертву быка, а по другим источникам, даже 100 быков. Это однако, противоречит сведениям о моральных и религиозных воззрениях Пифагора. В литературных источниках можно прочитать, что он «запрещал даже убивать животных ,а тем более ими кормиться, ибо животные имеют душу, как и мы».

Пифагор питался только мёдом, хлебом, овощами и рыбой. В связи со всем этим более правдоподобной можно считать: «…и даже когда он открыл, что в прямоугольном треугольнике гипотенуза имеет соответствие с катетами, он принес в жертву быка, сделанного из пшеничного теста».

Пребудет вечной истина, как скоро

Ее познает слабый человек!

И ныне теорема Пифагора

Верна, как и в его далёкий век.

Обильно было жертвоприношенье

Богам от Пифагора. Сто быков

Он отдал на закланье и сожженье

За света луч, пришедший с облаков.

Поэтому всегда с тех самых пор,

Чуть истина рождается на свет,

Быки ревут, ее почуя, вслед.

Они не в силах свету помешать.

А могут лишь, закрыв глаза, дрожать

От страха, что вселил в них Пифагор.

К теореме Пифагора его ученики составляли стишки, вроде:

«Пифагоровы штаны во все стороны равны»

А также рисовали такие карикатуры:

Доказательство теоремы считалось в кругах учащихся

средних веков очень трудным и называлось:

а сама теорема –

Чертёж к ней напоминал пчелу

Можно проследить связь слов «Пчела» — «нимфа» — «невеста», так и появилось название.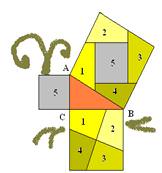

Уделом истины не может быть забвенье
Как только мир ее увидит взор,
И теорема та, что дал нам Пифагор,
Верна теперь, как в день ее рождения.

Учитель. Итак, об одном из самых таинственных героев особой , поворотной эпохи мы сегодня говорим. Пифагор создал самую яркую и самую современную «религию»: воспитал в человечестве веру в могущества разума, уверенность в том, что ключом к тайнам мировоззрения является математика. Музыка для Пифагора стала даже не средством вдохновения, а предметом научных изысканий, и именно в музыке Пифагор нашел прямое доказательство своему знаменитому тезису : «Все есть число» .Более 2500 лет тому назад Пифагор направил людей по пути торжества Разума.

Учитель музыки «Вклад Пифагора в музыку»

Учитель. Сегодня на нашей конференции представители прессы, телевидения. Представители различных газет и журналов.

Идет представление гостей:

Вопрос к представителю газеты «Советский спорт». В исторической справке о жизни и деятельности Пифагора было сообщение о том, что Пифагор участвовал в олимпийских играх. Не можете ли Вы сказать, каким видом спорта он занимался?

Ответ. Да. Пифагор был Олимпийским чемпионом по кулачному бою. Кстати, во времена жизни и деятельности Пифагора, очень часто научные споры решались с помощью кулачных боев.

Вопрос к представителю популярного молодежного журнала «Ровесник».

Ознакомившись с доказательством теоремы Пифагора, которое дано в учебнике, как вы считаете, доступно ли оно будет для ваших читателей?

Ответ. Мы считаем, что доказательство доступно, но для слабоуспевающих учеников такие вопросы в тексте доказательства, как — «докажите, почему?», «откуда это следует» — усложняют доказательство теоремы и, я думаю, их надо избегать.

Вопрос к журналу « Вопросы истории ». Мы часто в литературе встречаемся с такой фразой — « Пифагор Самосский ». Откуда возникло это название Пифагора?

Ответ. Его прозвали Пифагором Самосским потому, что он родился на острове Самосе.

Вопрос к представителям журнала «Архитектура и строительство». Находит ли теорема Пифагора применение в строительстве?

Ответ. Эта теорема применяется очень давно в нашем деле, ещё с построения Египетских пирамид и актуальна в современном строительстве, т. к. высота неразрывно связана с прямым углом, т: е. прямоугольным треугольником.

Вопрос к журналу «Семья и школа». Что интересного ваш журнал может посоветовать современной школе из жизни и деятельности Пифагора?

Ответ. Мы обратили внимание на одну особенность приема в Пифагорову школу, о которой сообщалось в исторической справке. Он принимал в свою школу только тех юношей, которые промолчали в течение пяти лет. Значит, при занятиях математикой нужна абсолютная тишина для того, чтобы можно было сосредоточить все внимание на решении того или другого утверждения.

Вопрос к представителям передачи Ц. Т. «Музыкальный киоск». Среди представителей технических и исторических журналов присутствие муз очень удивляет. Неужели имя Пифагора связано и с вашей деятельностью?

Ответ. Представьте себе, да. Пифагорийцы, исходя из своих наблюдений над металлическими пластинами, установили числовые соотношения, характерные для кварты (4/3), квинты (3/2) и октавы (2/1). Полутоны, тоны и ещё меньшие части тона были осознаны у пифагорийцев с точностью, превышающей точность новоевропейской акустики.

Вопрос к представителям передачи «Вокруг смеха». Мы знаем, что в результате доказательства этой теоремы она получила название «Пифагоровы штаны». Не натолкнула ли вас эта теорема на создание новых «шедевров» в области сатиры и юмора?

Ответ. Вчера пошла я в школу ст.Погрузная в 8 класс на урок геометрии. Села я на самом почетном, среди учеников, месте — сзади, по жаргону школьников «на Камчатку». Ну, а сегодня «самый сложный урок года» — как говорили мне сами ребята. Еще бы, ведь им нужно было доказать теорему Пифагора, формулу Герона. Боже мой! В 8-м классе — уже теоремы: да им еще сказки перед сном читать надо. А они теоремы доказывают. Учительница у них – Степанова Галина Алексеевна — очень строгий педагог. В отличие от некоторых, на её уроке не увидишь спящего ученика или расчесывающуюся ученицу. Поэтому ребята с удовольствием посещает ее уроки . Звенит звонок. Галина Алексеевна входит в класс, как всегда с улыбкой на лице, но улыбка сразу же исчезает с её лица, когда к доске выходит Синицын Саша. Текст теоремы он сформулировал так: «Пифагоровы штаны во все стороны равны». Но не успел он начать доказывать на своих только что сшитых по «Пифагору» модных штанах, как в клеточке журнала против его фамилии засветилась пара. Да, расстроилась ученица, да и учительница тоже. Наташа Михалченко вышла к доске, но ничего не может сказать. «Как формулируется текст теоремы?» — спросила Галина Алексеевна. «Конечно же. с выражением» — весело сказала в ответ ученица. «Ну что, может мы послушаем Егорова?» — спросила. Сергей и не думал идти к доске. Но когда ребята и учительница стали уговаривать его такими ласковыми словами, что от такого числа поклонников он не мог не ответить. С серьезным выражением лица он вышел к доске и быстро отрапортовал 1-й признак равенства треугольников .Галина Алексеевна была потрясена ответом ученика — «Молодец», ты хорошо выучил 1-й признак равенства треугольников, который вы учили в 7-м классе. И тут прозвенел долгожданный звонок.

Учитель Итак, сегодня мы много узнали о жизни Пифагора, о его знаменитой теореме. Знатоки утверждают, что теорема Пифагора популярна по трем причинам:

1)простота;

2) красота;

3) значимость.

И мы с вами сегодня в этом убедились. Вы показали себя знатоками теоремы Пифагора, любознательными учениками, умеющими думать. Спасибо всем за активное участие в конференции.

А теперь оцените в 10-бальной системе конференцию. Прежде чем оценить, ответьте для себя на вопросы:

1.  Узнали ли что-то новое?

2.  Заинтересовало ли вас содержание проектов?

3.  Довольны ли вы своей работой сегодня?

Учащиеся получают анкеты:

1.Выступление какой группы тебе больше всего понравилось?

«Историки»

«Исследователи»

«Теоретики»

«Практики»

«Лирики»

2.Оцени свой вклад в работу своей группы.