Хостинг документов » 4 класс » Конспект урока по Геометрии «Круг. Окружность» 4 класс

Конспект урока по Геометрии «Круг. Окружность» 4 класс

Тема: Круг. Окружность.

Цели и задачи урока: Развивать вычислительные навыки, внимание, логическое мышление, память. Воспитывать трудолюбие, дисциплинированность; товарищество, аккуратность. Познакомить с новыми понятиями (круг, окружность, радиус). Учить пользоваться циркулем для вычерчивания окружности.

Стадия

Методы	Ход урока.
Вызов	сравнение картинок	рассмотрите картинки, разделите на 2 группы. по какому признаку вы их разделили? кто догадался, какова тема урока? Чтобы уточнить тему, необходимо разгадать шифровку. Круг. Окружность. 783∙54 106∙18 344∙84 406∙27 8214∙42 206∙35 308∙24 902∙61 184920: 184 546182:182 169976:169 585168:146 18кг 600г 20кг 3ц 29ц100кг давайте предположим, чем мы будем заниматься на уроке.
Осмысление содержания	Верю не верю. Чтение с пометками Ромашка Блума подсказка	Какие предметы имеют форму круга, а какие окружности, распределить на доске. Деление на 2 группы. Что вы знаете об окружности? Посол. Игра “Верю-не верю” Приложение 1 Цель игры: Вызвать интерес к изучению темы “окружность”, создать положительную мотивацию самостоятельного изучения текста по теме. + знаю — хотел бы узнать ? не знаю приложение 2 составление вопросов (Приложение 3) посол собери утверждения. (приложение 4) С помощью чего можно изобразить круг? У каждой фигуры есть свой алгоритм построения. У окружности он тоже имеется. Попробуйте его выявить с помощью практической работы. сравнить с данными учителя. (приложение5) Отметьте в тетради точку и назовите её буквой О. Возьмите циркуль , раздвиньте «ножки» циркуля на заданном расстоянии. Поставьте иголку циркуля в точку О, а другой «ножкой» циркуля проведите замкнутую линию.
Рефлексия	чтение с пометками Исследовательская работа. Синквейн	Логическая задача. (Приложение 6) Карточка чтение с пометками. Еще раз проработайте. стр 269 № 10 математический диктант. Приложение 7
		Домашняя работа стр 268 №1 устно.

Приложение 1

Вопрос

“+” верю, “-” не верю
1. Верите ли вы, что самая простая из кривых линий – окружность?
2. Верите ли вы, что древние индийцы считали самым важным элементом окружности радиус, хотя не знали такого слова?
3. Верите ли вы, что впервые термин “радиус” встречается лишь в 16 веке?
4. Верите ли вы, что в переводе с латинского радиус означает “луч”?
5. Верите ли вы, что в русском языке слово “круглый” означает высшую степень чего-либо?

Приложение 1

Вопрос

“+” верю, “-” не верю
1. Верите ли вы, что самая простая из кривых линий – окружность?
2. Верите ли вы, что древние индийцы считали самым важным элементом окружности радиус, хотя не знали такого слова?
3. Верите ли вы, что впервые термин “радиус” встречается лишь в 16 веке?
4. Верите ли вы, что в переводе с латинского радиус означает “луч”?
5. Верите ли вы, что в русском языке слово “круглый” означает высшую степень чего-либо?

Свежие документы: Урок геометрии для 7 класса на тему "Медиана, биссектриса и высота треугольника"

Приложение 1

Вопрос

“+” верю, “-” не верю
1. Верите ли вы, что самая простая из кривых линий – окружность?
2. Верите ли вы, что древние индийцы считали самым важным элементом окружности радиус, хотя не знали такого слова?
3. Верите ли вы, что впервые термин “радиус” встречается лишь в 16 веке?
4. Верите ли вы, что в переводе с латинского радиус означает “луч”?
5. Верите ли вы, что в русском языке слово “круглый” означает высшую степень чего-либо?

Приложение 2

У круга есть одна подруга,

Знакома всем ее наружность,

Она идет по краю круга,

И называется окружность.

Круг Окружность

Самая простая из кривых линий – окружность. Это одна из древнейших геометрических фигур.

Ещё вавилоняне и древние индийцы считали самым важным элементом окружности – радиус. Слово это латинское и означает “луч”. В древности не было этого термина: Евклид и другие учёные говорили просто “прямая из центра”.

ОМ – радиус

Термин “радиус” становится лишь в конце XVII в. Впервые термин “радиус” встречается в “Геометрии” французского ученого Рамса, изданной в 1569 году.

В Древней Греции круг и окружность считались венцом совершенства.

В русском языке слово “круглый” тоже стало означать высокую степень чего-либо: “круглый отличник”, “круглый сирота” и даже “круглый дурак”.

Без понятия круга и окружности было бы трудно говорить о круговращении жизни. Круги повсюду вокруг нас.

Приложение 3

Что?

Кто?

Где?

Когда?

Почему?

Зачем?

Приложение 3

Что?

Кто?

Где?

Когда?

Почему?

Зачем?

Приложение 3

Что?

Кто?

Где?

Когда?

Почему?

Зачем?

Приложение 3

Что?

Кто?

Где?

Когда?

Почему?

Зачем?

Приложение 4

Окружность – замкнутая линия…

… все точки которые находятся на одинаковом расстоянии от центра.

Круг – это часть плоскости…

… ограниченная окружностью.

Радиус – это отрезок, соединяющий…

… соединяющий центр окружности с любой точкой на окружности.

Приложение 4

Окружность – замкнутая линия…

… все точки которые находятся на одинаковом расстоянии от центра.

Круг – это часть плоскости…

… ограниченная окружностью.

Радиус – это отрезок, соединяющий…

… соединяющий центр окружности с любой точкой на окружности.

Свежие документы: Конспект урока по Геометрии "Оригами" 6 класс

Приложение 5

Отметьте в тетради точку и назовите её буквой О.
Возьмите циркуль , раздвиньте «ножки» циркуля на заданном расстоянии.
Поставьте иголку циркуля в точку О, а другой «ножкой» циркуля проведите замкнутую линию.

Приложение 5

Отметьте в тетради точку и назовите её буквой О.
Возьмите циркуль , раздвиньте «ножки» циркуля на заданном расстоянии.
Поставьте иголку циркуля в точку О, а другой «ножкой» циркуля проведите замкнутую линию.

Приложение 5

Отметьте в тетради точку и назовите её буквой О.
Возьмите циркуль , раздвиньте «ножки» циркуля на заданном расстоянии.
Поставьте иголку циркуля в точку О, а другой «ножкой» циркуля проведите замкнутую линию.

Приложение 5

Отметьте в тетради точку и назовите её буквой О.
Возьмите циркуль , раздвиньте «ножки» циркуля на заданном расстоянии.
Поставьте иголку циркуля в точку О, а другой «ножкой» циркуля проведите замкнутую линию.

Приложение 5

Отметьте в тетради точку и назовите её буквой О.
Возьмите циркуль , раздвиньте «ножки» циркуля на заданном расстоянии.
Поставьте иголку циркуля в точку О, а другой «ножкой» циркуля проведите замкнутую линию.

Приложение 6

Не нарушая закономерностей, построй радиусы в последних окружностях:

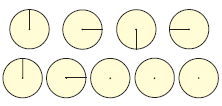
Приложение 6

Не нарушая закономерностей, построй радиусы в последних окружностях:

Приложение 7

Нарисуйте две окружности, которые имеют одну общую точку. Измерьте длины их радиусов
Нарисуйте две окружности, которые пересекаются в двух точках. Измерьте длины их радиусов.

Приложение 7

Нарисуйте две окружности, которые имеют одну общую точку. Измерьте длины их радиусов
Нарисуйте две окружности, которые пересекаются в двух точках. Измерьте длины их радиусов.

Рабочий лист.

Ф.И. ___________________________________________ дата __________________

Задание 1

Прочитай. Сделай пометки:

+ знаю

— хотел бы узнать

? не знаю

У круга есть одна подруга,

Знакома всем ее наружность,

Она идет по краю круга,

И называется окружность.

Круг Окружность

Самая простая из кривых линий – окружность. Это одна из древнейших геометрических фигур.

ОМ – радиус

В Древней Греции круг и окружность считались венцом совершенства.

Без понятия круга и окружности было бы трудно говорить о круговращении жизни. Круги повсюду вокруг нас.

Задание 2

Алгоритм

Задание 3

Не нарушая закономерностей, построй радиусы в последних окружностях:

Задание 4

Исследовательская работа.

Нарисуйте две окружности, которые имеют одну общую точку. Измерьте длины их радиусов.

Нарисуйте две окружности, которые пересекаются в двух точках. Измерьте длины их радиусов.

Самоанализ урока по математике на тему: Круг. Окружность. 4 класс.

Методической целью данного урока было показать особенности построения урока по технологии критического мышления. Рассмотреть некоторые стратегии данной технологии, возможности их применения на различных этапах урока и особенности применения их на других уроках.

Что же такое критическое мышление?
КМ – под этим понятием подразумевается самостоятельное мышление, где отправной точкой является информация. Оно начинается от постановки вопросов, строится на основе убедительной аргументации.

Особенностью данной педагогической технологии является то, что учащийся в процессе обучения сам конструирует этот процесс, исходя из реальных и конкретных целей, сам отслеживает направления своего развития, сам определяет конечный результат. С другой стороны, использование данной стратегии ориентировано на развитие навыков вдумчивой работы с информацией, с текстом.

Определения КМ обычно включает в себя умение прогнозировать ситуацию, наблюдать, обобщать, сравнивать, выдвигать гипотезы и устанавливать связи, рассуждать по аналогии и выявлять причины, а также предполагает рациональный и творческий подход к рассмотрению любых вопросов.

Восприятие информации происходит в три этапа, что соответствует таким стадиям урока:

подготовительный – стадия вызова;
восприятие нового – смысловая стадия (или стадия реализации смысла);
присвоение информации – стадия рефлексии.

Стадия

Функции
Вызов	Мотивационная (побуждение к работе с новой информацией, стимулирование интереса к новой теме). Информационная (вызов на «поверхность» имеющихся знаний по теме. Коммуникационная (бесконфликтный обмен мнениями).
Осмысление содержания	Информационная (получение новой информации по теме). Систематизационная (классификация полученной информации). Мотивационная (сохранения интереса к изучаемой теме).
Рефлексия	Коммуникационная (обмен мнениями о новой информации). Информационная (приобретение нового знания). Мотивационная (побуждение к дальнейшему расширению информационного поля). Оценочная (соотнесение новой информации и имеющихся знаний, выработка собственной позиции, оценка процесса).

Формы урока в РКМЧП отличаются от уроков в традиционном обучении. Ученики не сидят пассивно, слушая учителя, а становятся главными действующими лицами урока. Они думают и вспоминают про себя, делятся рассуждениями друг с другом, читают, пишут, обсуждают прочитанное. Тексту отводится приоритетная роль: его читают, пересказывают, анализируют, трансформируют, интерпретируют, дискутируют, наконец, сочиняют.
Роль учителя — в основном координирующая.

В технологии критического мышления существует множество методических приемов для реализации целей разных фаз базовой модели урока. Некоторые из них представлены в уроке.