Хостинг документов » 7 класс » Конспект урока по геометрии в 7 классе «Сумма углов треугольника»

Конспект урока по геометрии в 7 классе «Сумма углов треугольника»

КГУ «Первомайский комплекс «Общеобразовательная средняя школа-детский сад имени Д. М. Карбышева» отдела образования Шемонаихинского района»

Конспект урока по геометрии
в 7 классе

«Сумма углов треугольника»

подготовила

учитель математики

Беляева Елена Валерьевна

п. Первомайский,

2013

Открытый урок по теме: «Сумма углов треугольника»

Я предлагаю проверить всё ли имеется у вас на рабочих местах, что потребуется нам сегодня на уроке: рабочая тетрадь, ручка, карандаш, линейка, кроме того у вас на столах лежит необычный предмет, тайну которого мы откроем сегодня на уроке

Девиз: Да, путь познания не гладок,

Но знаем мы со школьных лет,

Загадок больше, чем отгадок,

И поискам предела нет.

Цели:

Обучающие: Практическим путем выяснить чему равна сумма углов треугольника, познакомиться с формулировкой теоремы о сумме углов треугольника, доказать теорему, доказать следствия из теоремы, научиться применять изученную теорему при решении задач
Развивающие: развитие математической речи учащихся и творческой активности учащихся.
Воспитывающие: воспитание у учащихся аккуратности, внимательности, положительного отношения к математике.

Ход урока.

1. Организационный момент.

Учитель. Здравствуйте, ребята. Сегодня мы будем изучать новую тему, но для начала поработаем устно.

Повторение. Беседа по изученному материалу.

— Что такое треугольник? (треугольник – это фигура, образованная тремя точками, не лежащими на одной прямой, и отрезками, попарно соединяющими эти точки).

В руках у учителя модель треугольника, у которого 2 угла известны. Перед учащимися ставится задача: найти величину третьего угла.

Часто знает и дошкольник,

Что такое треугольник.

А уж вам – то как не знать…

Но совсем другое дело –

Очень быстро и умело

Величины всех углов

В треугольнике узнать.

Чтобы ответить на этот вопрос, нужно выяснить, чему равна сумма всех углов треугольника. Этим мы и займёмся сегодня на уроке.

— Какие треугольники различают по сторонам? (равнобедренный, равносторонний, разносторонний)

Треугольники классифицируют не только по сторонам, но и по углам. Сначала поговорим об углах.

— Что такое угол? (Угол – это фигура, образованная двумя лучами, выходящими из одной точки. Лучи называются сторонами угла, а точку – вершиной угла.)

— Какой угол называют прямым? (угол, величина которого равна 90º)

— Какой угол называют развёрнутым? (угол, величина которого равна 180º)

— Какой угол называют острым? (угол, величина которого меньше 90º.)

— Какой угол называют тупым? (угол, величина которого больше 90º, но меньше 180º)

Таким образом углы бывают острые, прямые, тупые, развёрнутые.

Если мы начертим в тетради три угла: острый, тупой и прямой. Дополним рисунок до треугольника. Какие получатся треугольники? (тупоугольный, прямоугольный, остроугольный)

— Откройте тетради, запишите число, тему урока: Сумма углов треугольника.

Треугольники бывают разные, их различают по сторонам и углам.

На каждой парте лежат по 3 равных треугольника.

Учитель. Перед вами на столе три равных треугольника. Как можно в этом убедиться?

Наложите один треугольник на другой, и вы проверите это.

Рисунок 2

Учитель. Положите желтый треугольник на стол, а два других треугольника положите рядом с первым таким образом, чтобы у одной вершины оказалось три разных угла, а стороны их совпадали.

Учитель помогает учащимся, а затем выполняет указанные действия на доске (треугольники крепятся при помощи магнитов).

Рисунок 3

Учитель. Посмотрите внимательно, что у вас получилось? Какой угол составляют вместе 1, 2 и 3? Какова градусная мера этого угла? Значит, чему равна сумма углов 1, 2 и 3? Чему равна сумма равных им углов желтого треугольника?

Обратите внимание, что я всем выдала разные треугольники (на каждой парте). Что у вас получилось? Какова сумма углов вашего желтого треугольника? Какой теперь мы можем сделать вывод о сумме углов треугольника?

Итак, мы выяснили практическим путем, что сумма углов треугольника равна 180.

Докажем теорему.

III. Доказательство теоремы о сумме углов треугольника.

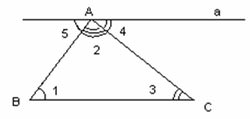
Дано: ABC
Доказать: 1+2+3=180^o
Доказательство:
1) Проведём а BC, А а
2) 5=1 – накрест лежащие углы при параллельных прямых а и ВС и секущей АВ.
3) 3=4 – накрест лежащие углы при параллельных прямых а и ВС и секущей АС.
4) 5+2+4=180^o (развёрнутый угол)
5) 1+ 2+ 3=180^o Теорема доказана.

Итак, 1) с помощью модели (путём практической работы) и…

3) путём строгого доказательства теоремы

мы пришли к выводу, что (отвечают ученики) сумма углов треугольника равна 180º.

— Как найти угол в треугольнике, если известны два других угла этого треугольника?

4. Решение задач.

1) Решение устных задач (чертеж проецируется на экран с помощью кодоскопа).

Найдите неизвестные углы треугольника (рис.5, рис.6)

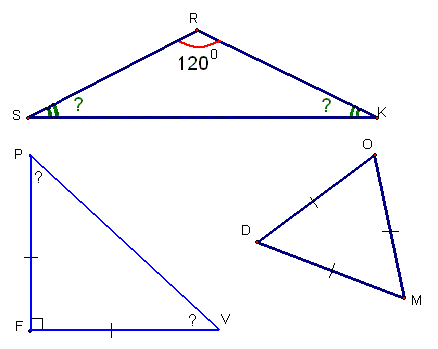
Рисунок 5 Рисунок 6

После устного рассмотрения задач в тетрадях записываются некоторые выводы:

В равностороннем треугольнике все углы равны 60.
В прямоугольном треугольнике сумма острых углов равна 90.
В прямоугольном равнобедренном треугольнике острые углы равны 45.

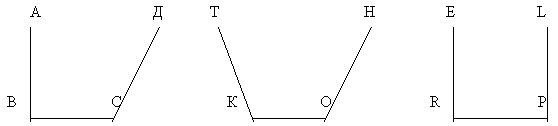
— Почему в треугольнике не может быть двух прямых углов?

— Почему в треугольнике не может быть двух тупых углов?

— Почему в треугольнике не может быть один тупой, а другой прямой угол?

3). Задача с записью в тетрадь.

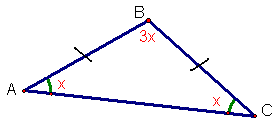
Найдите углы равнобедренного треугольника, если угол между боковыми сторонами в 3 раза больше угла при основании равнобедренного треугольника.

Дано: АВС – равнобедренный

АВ=ВС

В=3 А

___________________________

Найти: А, В, С

Рисунок 8

Решение:

Пусть А=х, тогда В = 3х.

А = С = х (так как АВС равнобедренный)

Зная, что сумма углов треугольника равна 180, составляем уравнение:

х + х + 3х = 180

5х = 180

х = 36

_____________

3х = 108.

Ответ: А = 36, В=36, С = 108.

5. Подведение итогов.

Учитель. Итак, ребята, мы заканчиваем наш урок. Вы сегодня хорошо потрудились. Сами открыли чему равна сумма углов треугольника, вместе доказали теорему, решали задачи. Так чему же равна сумма углов любого треугольника?

Запишите домашнее задание:

— выучить теорему п. 6.2, стр. 49;

— решить задачи №155, №163.

В конце урока выставляются оценки.

Список использованной литературы

Геометрия: Учебник для 7 класса общеобразовательной школы.- Алматы: Атамура, 2003.
Рабинович Е.М. Задачи и упражнения на готовых чертежах. 7-9 классы. Геометрия. – М.: Илекса, Харьков: Гимназия, 1998.
Шуба М.Ю. Занимательные задания в обучении математике: Кн. Для учителя. – М.: Просвещение, 1995.