Контрольная работа по геометрии

Геометрическое задание   ЕГЭ по математике базового уровня. Начнем с прямоугольного треугольника, ведь основная масса заданий связанна именно с ним. А значит надо знать теорему Пифагора, тригонометрические функции, тригонометрические тождества. Уметь составлять пропорцию.

По теореме Пифагора всегда можно найти третью сторону в прямоугольном треугольнике, зная две других. Сторона которая лежит напротив прямого угла называется гипотенузой, две другие — это катеты.

Например:

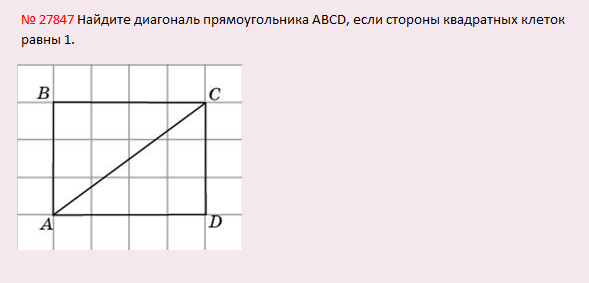
Решение: Диагональ АС является гипотенузой прямоугольного треугольника АВС или АСD (по сути все-равно, они ведь одинаковые).

Пусть, это будет треугольник АВС. Сторона АВ=3, ВС=4.

По теореме Пифагора найдем гипотенузу АС:

Достаточно много задач в ЕГЭ по математике 2012 задания В3, где в прямоугольном треугольнике необходимо найти sin, cos или tg угла.

Итак, по порядку:

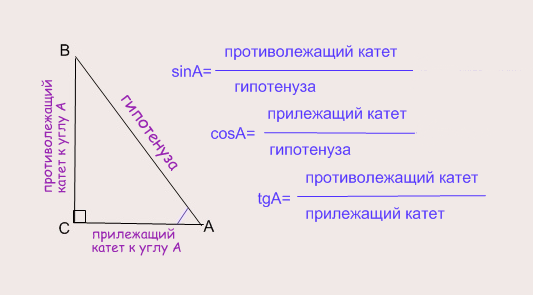
Обратите внимание на то, что для угла В прилежащий катет — это наоборот сторона ВС, а противолежащий катет — АС. Гипотенуза для любого угла  — это сторона АВ.

Например:

Решение: Данную задачу можно решать несколькими способами, но мы разберем способ с использованием теоремы Пифагора.

Итак, в задаче дан cosА, а это значит, что отношение прилежащего катета к гипотенузе равно корень из 55 делить на 8, следовательно прилежащий катет мы приравняем к корню из 55, умноженному на Х, а к гипотенузе — 8, умноженную на Х. т.е.:

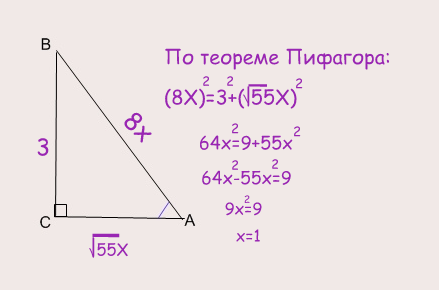
Следовательно, Ав=8х=8*1=8, ответ: 8

Разбирая задание В6 перейдем к задачам, где один треугольник содержит в себе прямоугольный треугольник: суть решения такая же, как описана выше.

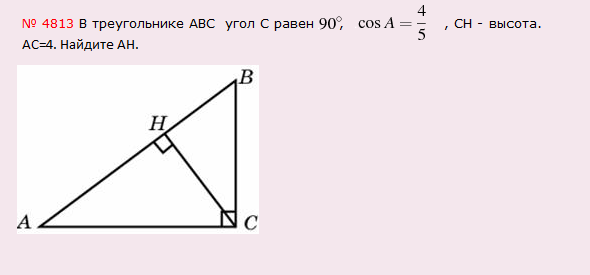
Решение: Треугольник АВС — прямоугольный, в нем проведена высота СН, а значит внутри треугольника АВС образуется еще один прямоугольный треугольник АСН. Вот его то мы и будем рассматривать. Т.к. сosА это отношение прилежащего катета к гипотенузе, где прилежащим катетом к углу А является сторона АН , а гипотенузой АС, то АН=4х, а АС=5х. В то же время по условию задачи АС=4:

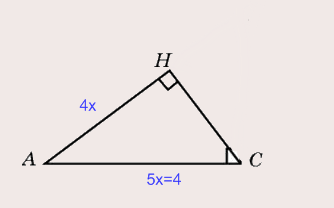
Следовательно 5х=4, а х=4/5 или х=0,8. Значит сторона АН=4*0,8=3,2.

В этой задаче внутри одного прямоугольного треугольника находился другой прямоугольный треугольник.

А теперь разберем задание, где прямоугольный треугольник образуется в равнобедренном:

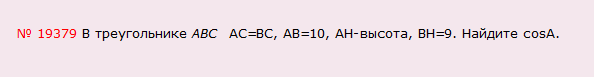
Решение: Треугольник АВС — равнобедренный, т.к. АС=ВС, а значит равны и углы при основании АВ, т.е. угол А равен углу В. Следовательно сosA=cosB. Рассмотрим прямоугольный треугольник АВН. Косинус — это прилежащий катет к гипотенузе. а значит cosB=9/10=0,9, а значит и сosA=0,9:

Для решения следующей задачи необходимо знать формулы приведения. На самом деле этих формул 32 штуки.

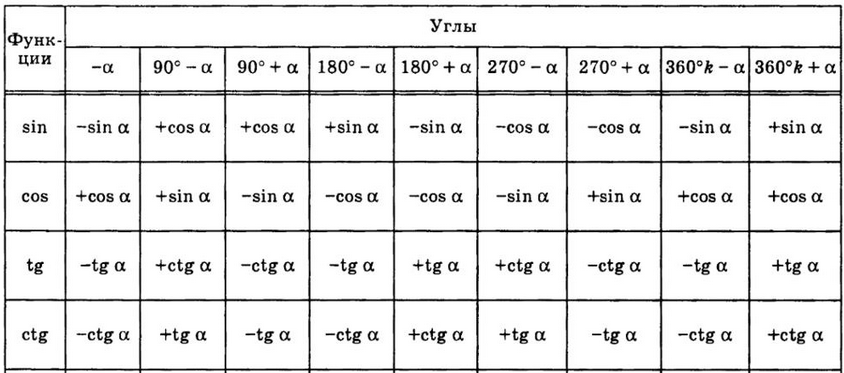
В данном задании может понадобиться всего две:

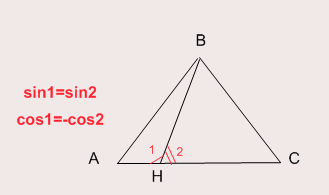
Разберем еще одну задачу:

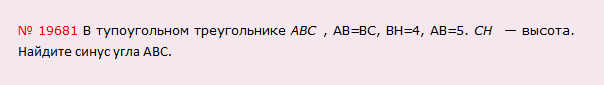
Решение: Для начала нарисуем этот тупоугольный треугольник:

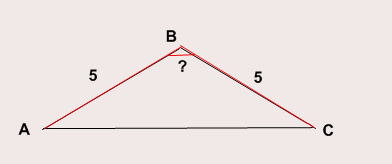
А теперь проведем высоту СН. Т.к. высота должна падать под углом в 90 градусов, то СН под этим углом к прямой АВ придется откладывать не на самую прямую АВ, а на ее продолжение:

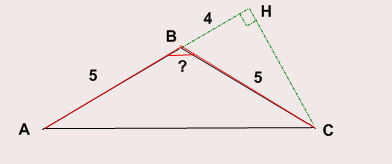
Итак, образовался прямоугольный треугольник ВСН. По условию задачи необходимо рассчитать sin В. По формулам приведения он равен sin СВН. Поэтому будем искать сначала sin CВН. Синус — это отношение противолежащего катета НС к гипотенузе ВС. НС нам не известно, а ВС=5. По теореме Пифагора найдем НС :

ВН²+НС²=ВС²

НС²=ВС²-ВН²

НС²=5²-4²=9

НС=3

Следовательно:

Sin НВС=3/5=0,6.

Продолжая тему подготовки к ЕГЭ, поговорим о четырехугольниках: трапециях и параллелограммах.

Разберем на примере:

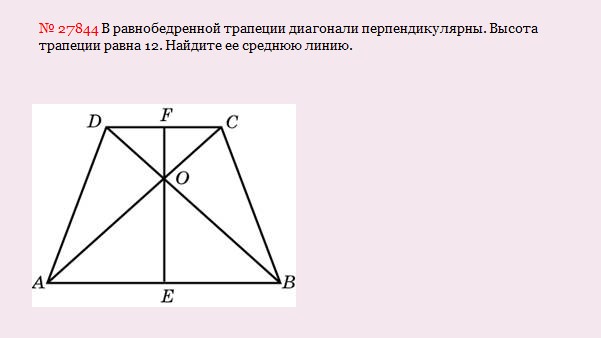
Решение: Средняя линия трапеции равна половине суммы оснований. Т.е. надо знать чему равны основания АВ и CD. Диагонали пересекаются под углами в 90 градусов, следовательно образуются 4 прямоугольных равнобедренных треугольника: DFO, FCO, AOE, EOB:

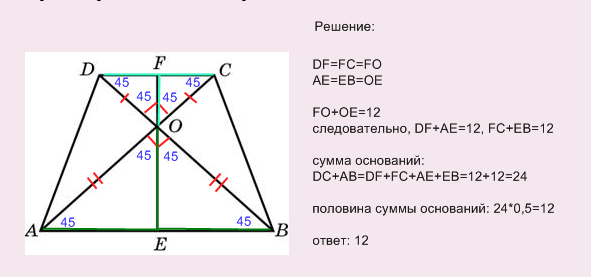
Разберем еще одну задачу:

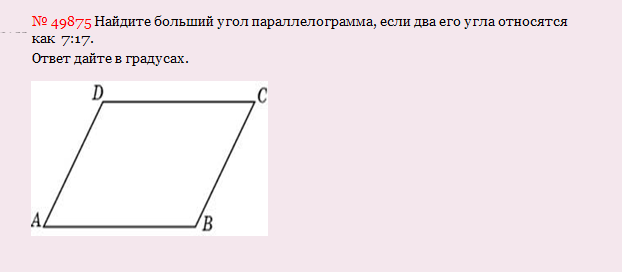
Решение: Больший угол — это угол D или В. Т.к. углы относятся как

7 к 17, то пусть угол А= 7х, а угол D=17x. Сумма этих углов 180 градусов, следовательно 7х+17х=180, 24х=180, х=7,5, а угол D=7,5*17=127,5

В базе ЕГЭ по математике 2012  встречаются и задачи на тему вписанных и описанных окружностей, поэтому стоит обратить на это особое внимание.

Вписанные окружность — это окружность, которая вписаны внутри многоугольника и важно, чтобы каждая вершина многоугольника касалась окружности.

Описанная окружность — это окружность, которая описана около многоугольника и важно, чтобы каждая вершина многоугольника касалась окружности.

Сначала немного об окружностях:

Например, внутренний угол АСВ в два раза меньше центрального угла АОВ, оба угла опираются на дугу АВ.

Разберем на примере:

Решение: На дугу АВ опираются два угла: внутренний АСВ и центральный АОВ, значит центральный угол в два раза больше вписанного, а значит равен 16*2=32 градуса. Т.к. DВ — диаметр, то углы DOA и АОВ — смежные, а значит в сумме равны 180 градусов, если угол АОВ=32, то угол DOB=180-32=148 градусов.

Разберем еще один пример:

Решение: Проведем радиусы ВО и АО, полученный треугольник АВО — равнобедренный:

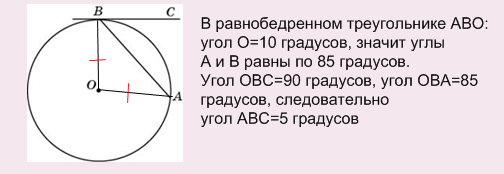
В одном из вариантов диагностической работы за 3 марта 2011 года была предложена такая задача В6, которая вызвала у многих сложность, поэтому хочу сегодня разобрать решения подобных ей задач.

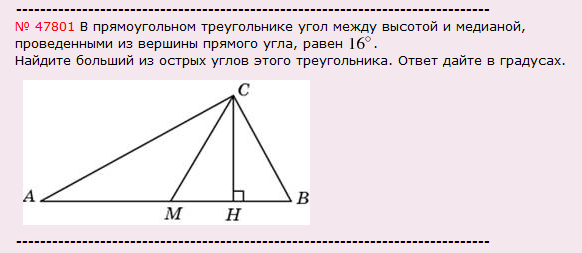
Решение: В данной задаче даны медиана и высота. Задача не такая уж и сложная, но при условии, если вы помните, что медиана, выходящая из прямого угла равна половине гипотенузы. В нашем случае, это значит, что АМ=МВ=СМ. Следовательно треугольники АМС и МСВ — равнобедренные, а значит углы при основании этих треугольников тоже равны. Я обозначила их за х и y:

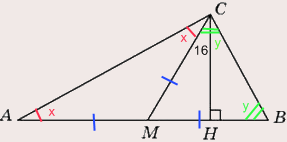
Рассмотри прямой угол С (х+y=90). Угол ВСH=90-y, в то же время угол BCH=y-16 (т.к. СH — высота). Приравняем: 90-y=y-16. Следовательно, 2y=106, y=54. Значит х=90-54=36. Больший из острых углов равен 54.

Рассмотрим еще одну задачу:

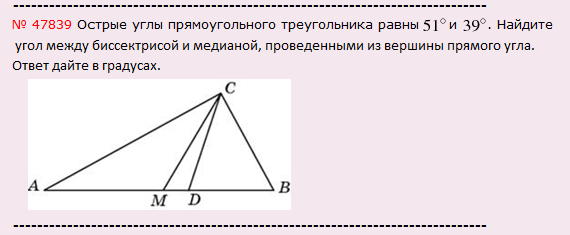
Решение: В данной задаче даны медиана и биссектриса. Медиана из прямого угла в этой задаче тоже равна половине гипотенузы. Значит, что АМ=МВ=СМ. Следовательно треугольники АМС и МСВ — равнобедренные, а значит углы при основании этих треугольников тоже равны:

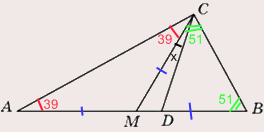
Т.к. CD — биссектриса, то углы ВСD и АСD равны. Это значит 39+х=51, значит х=51-39, х=12.