Невозможные треугольники, 6 класс

МБСКОУ СКОШ № 36

г. Озерска Челябинской области

Невозможный треугольник

выполнил Кормаков Никита,

ученик 6 класса

руководитель

Клокова Татьяна Юрьевна,

учитель математики

Содержание

1.Введение ………………………………………………….……3

Актуальность: Математика – предмет, изучающийся с первого по выпускной класс. Многие ученики считают его сложным, неинтересным и ненужным. Но если заглянуть за страницы учебника, почитать дополнительную литературу, математические софизмы и парадоксы, то изменится представление о математике, появится желание изучать больше, чем изучается в школьном курсе математики.

Цель работы:

показать, что существование невозможных фигур расширят кругозор, развивает пространственное воображение, применяется не только математиками, но и художниками.

Задачи:

1. Изучить литературу по данной теме.

2. Рассмотреть невозможные фигуры, сделать модель невозможного треугольника, доказать, что невозможный треугольник не существует на плоскости.

3. Сделать развертку невозможного треугольника.

4. Рассмотреть примеры использования невозможного треугольника в изобразительном искусстве.

Введение

Исторически, математика играла важную роль в изобразительном искусстве, в частности при изображении перспективы, подразумевающем реалистичное изображение трехмерной сцены на плоском холсте или листе бумаги. Согласно современным взглядам, математика и изобразительное искусство очень удаленные друг от друга дисциплины, первая — аналитическая, вторая — эмоциональная. Математика не играет очевидной роли в большинстве работ современного искусства, и, фактически, многие художники редко или вообще никогда не используют даже использование перспективы. Однако, есть много художников, у которых математика находится в центре внимания. Несколько значительных фигур в изобразительном искусстве проложили дорогу этим индивидуумам.

Вообще-то не существует каких-либо правил или ограничений на использование различных тем в математическом искусстве, таких как, невозможные фигуры, лента Мебиуса, искажение или необычные системы перспективы, а также фракталы.

История невозможных фигур

Невозможные фигуры — определённый вид математических парадоксов, состоящих из регулярных деталей, соединённых в нерегулярном комплексе. Если попытаться сформулировать определение термина «невозможные объекты» он бы, наверно, звучал примерно так — физически возможные фигуры, собранные в невозможном виде. Но смотреть на них гораздо приятнее, составления определений.

Ошибки пространственного построения встречались у художников и тысячу лет тому назад. Но первым построившим и проанализировавшим невозможные объекты по праву считается шведский художник Оскар Рейтерсвэрд, нарисовавший в 1934г. первый невозможный треугольник, состоявший из девяти кубиков.

Треугольник Рейтерсвэрда

Независимо от Рейтерсвэрда английский математик и физик Роджер Пенроуз повторно открывает невозможный треугольник и публикует его изображение в британском журнале по психологии в 1958г. В иллюзии использована «ложная перспектива». Иногда такую перспективу называют китайской, так как подобный способ рисования, когда глубина рисунка «двусмысленна», часто встречался в работах китайских художников.

Водопад Эшера

В 1961г. голландец М. Эшер, вдохновленный невозможным треугольником Пенроуза, создает известную литографию «Водопад». Вода на картине течет бесконечно, после водяного колеса она проходит дальше и попадает обратно в исходную точку. По сути, это изображение вечного двигателя, но любая попытка в реальности построить данную конструкцию обречена на неудачу.

Еще один пример невозможных фигур представлен на рисунке «Москва», на котором изображена не совсем обычная схема московского метрополитена. Сначала мы воспринимаем изображение целиком, но прослеживая взглядом отдельные линии, убеждаемся в невозможности их существования.

«Москва», графика (тушь, карандаш), 50х70 см, 2003 г.

Рисунок «Три улитки» продолжает традиции второй знаменитой невозможной фигуры — невозможного куба (ящика).

«Три улитки» Невозможный куб

Дональд Симанек высказал мнение, что понимание визуальных парадоксов является одним из признаков того вида творческого потенциала, которым обладают лучшие математики, ученые и художники. Многие работы с парадоксальными объектами можно отнести к «интеллектуальным математическим играм». Современная наука говорит о 7-мерной или 26-мерной модели мира. Моделировать подобный мир можно только с помощью математических формул, человек представить его просто не в состоянии. И здесь оказываются полезными невозможные фигуры.

Третьей популярной невозможной фигурой является невероятная лестница, созданная Пенроузом. Вы будете по ней непрерывно или подниматься (против часовой стрелки) или спускаться (по часовой стрелке). Модель Пенроуза легла в основу знаменитой картины М. Эшера «Вверх и вниз» Невероятная лестница Пенроуза

Невозможный трезубец

«Чертова вилка»

Существует еще одна группа объектов, реализовать которые не получится. Классической фигурой является невозможный трезубец, или «чертова вилка». При внимательном изучении картинки можно заметить, что три зубца постепенно переходят в два на едином основании, что приводит к конфликту. Мы сравниваем количество зубцов сверху и снизу и приходим к выводу о невозможности объекта. Если закрыть рукой верхнюю часть трезубца, то мы увидим вполне реальную картину — три круглых зуба. Если закрыть нижнюю часть трезубца, то мы тоже увидим реальную картину — два прямоугольных зубца. Но, если рассматривать всю фигуру целиком, то получается что три круглых зубца постепенно превращаются в два прямоугольных.

Таким образом, можно увидеть, что передний и задний планы данного рисунка конфликтуют. То есть, то, что было изначально на переднем плане уходит назад, а задний план (средний зуб) вылезает вперед. Кроме смены переднего и заднего планов в данном рисунке присутствует еще один эффект  – плоские грани верхней части трезубца становятся круглыми в нижней части.

Основная часть.

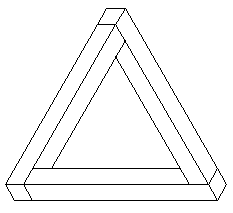
Треугольник – фигура, состоящая из 3-х примыкающих частей , которая с помощью неприемлемых соединений этих частей создаёт иллюзию с математической точки зрения невозможной структуры. По-другому ещё этот трехбалочник называют угольником Пенроузов

Графический принцип, скрывающийся за этой иллюзией, обязан своей формулировкой психологу Л.С. Пенроузу и его сыну Роджеру, физику. Угольник Пенрузов состоит из 3-х брусков квадратного сечения, расположенных в 3-х взаимно-перпендикулярных направлениях ; каждый соединяется со следующим под прямым углом , всё это помещается в трёхмерном пространстве . Вот простой рецепт , как нарисовать эту изометрическую проекцию угольника Пенрузов:

• Обрежьте углы у равностороннего треугольника по линиям, параллельным сторонам;

• Проведите внутри обрезанного треугольника параллели к сторонам;

• Ещё раз обрежьте углы;

• Ещё раз проведите внутри параллели;

• Представьте себе в одном из углов какой-нибудь из двух возможных кубов;

• Продолжите его L — образной “штукой”;

• Прогоните эту конструкцию по кругу.

• Если бы мы выбрали другой куб, то угольник был бы “закручен” в другую сторону.

Развертка невозможного треугольника.

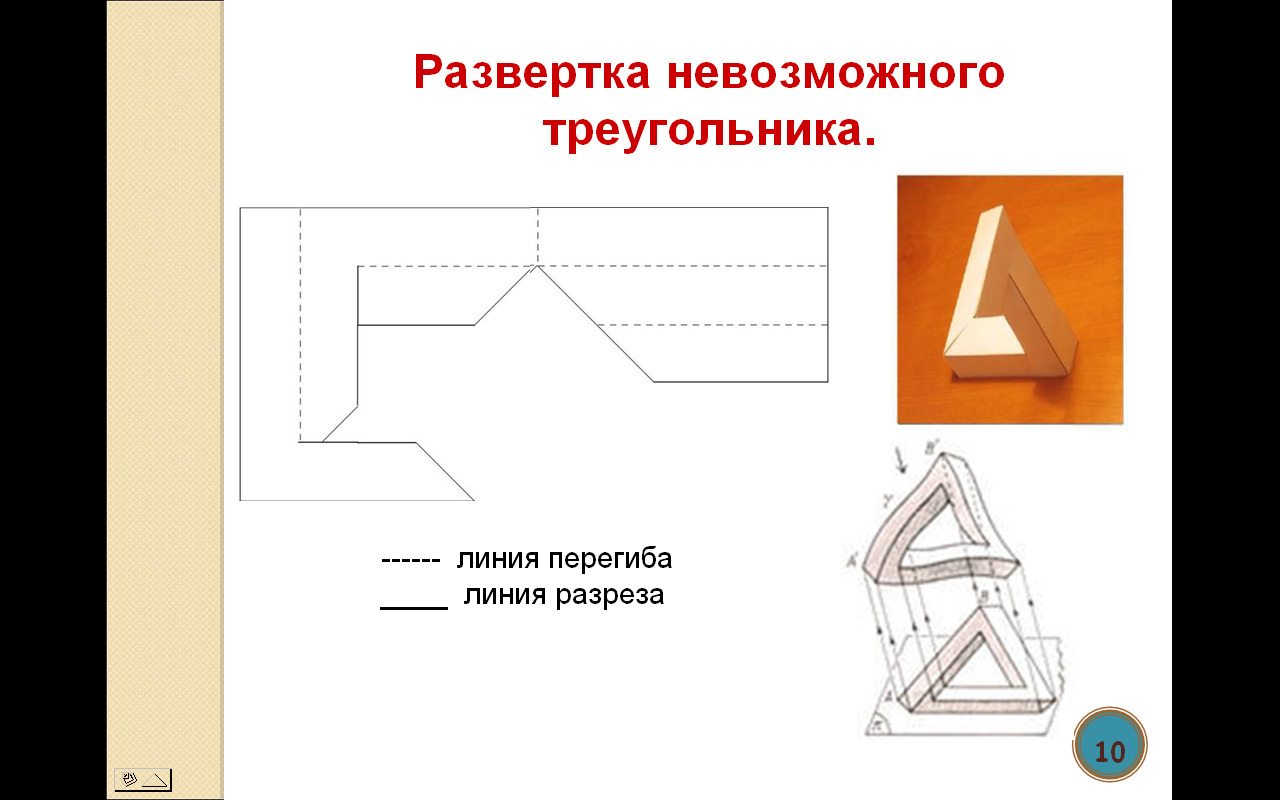
—— линия перегиба

____ линия разреза

Из каких элементов строится невозможный треугольник? Точнее, из каких элементов он кажется нам (именно кажется!) построенным? В основе конструкции лежит прямоугольный уголок, который получается соединением под прямым углом двух одинаковых прямоугольных брусков. Таких уголков требуется три штуки, а брусков, стало быть, шесть штук. Эти уголки надо определенным образом зрительно «соединить» один с другим так, чтобы они образовали замкнутую цепь. То, что получится, и есть невозможный треугольник.

Первый уголок поместим в горизонтальной плоскости. К нему присоединим второй уголок, направив одно из его ребер вверх. Наконец, к этому второму уголку пристроим третий уголок так, чтобы его ребро было параллельно исходной горизонтальной плоскости. При этом два ребра первого и третьего уголков будут параллельны и направлены в разные стороны.

А теперь попробуем мылено посмотреть на фигуру из разных точек пространства (или сделайте реальный макет из проволоки). Представьте, как она выглядит из одной точки, из другой, из третьей… При изменении точки наблюдения (или – что то же самое – при повороте конструкции в пространстве) будет казаться, что два «концевых» ребра наших уголков перемещаются относительно друг друга. Нетрудно подобрать такое положение, при котором они соединятся (конечно, при этом ближний уголок будет казаться нам толще, чем более длинный).

Но если расстояние между ребрами намного меньше расстояния от уголков до точки, из которой мы рассматриваем нашу конструкцию, то оба ребра будут иметь для нас одинаковую толщину, и возникнет представление о том, что эти два ребра – на самом деле продолжение один другого.

Кстати, если мы одновременно посмотрим на отображение конструкции в зеркале, то там замкнутой цепи не увидим.

А из выбранной точки наблюдения мы собственными глазами видим свершившееся чудо: имеется замкнутая цепь из трех уголков. Только не меняйте точку наблюдения, чтобы эта иллюзия (на самом деле именно иллюзия!) не разрушилась. Теперь можно нарисовать видимый вам объект или поместить в найденную точку объектив фотоаппарата и получить фотографию невозможного объекта.

Первыми этим явлением заинтересовались Пенроузы. Они использовали возможности, которые возникают при отображении трехмерного пространства и трехмерных объектов на двумерную плоскость (то есть при проектировании) и обратили внимание на некоторую неопределенность проектирования – незамкнутая конструкция из трех уголков может восприниматься как замкнутая цепь.

Как уже говорилось, из проволоки можно легко изготовить простейшую модель, в принципе поясняющую наблюдаемый эффект. Возьмите прямолинейный кусок проволоки и разделите его на три равные части. Затем согните крайние части так, чтобы они образовали прямой угол со средней частью, и поверните друг относительно друга на 90 . Теперь поворачивайте эту фигурку и наблюдайте за ней одним глазом. При некотором ее положении будет казаться, что она образована из замкнутого куска проволоки. Включив настольную лампу, можно понаблюдать за тенью, падающей на стол, которая также при определенном расположении фигуры в пространстве превращается в треугольник.

Впрочем, эту особенность проектирования можно наблюдать и в другой ситуации. Если сделать кольцо из проволоки, а затем его развести в разные стороны, то получится один виток цилиндрической спирали. Этот виток, разумеется , разомкнут. Но при проектировании его на плоскость можно получить замкнутую линию.

Мы еще раз убедились, что по проекции на плоскость, по рисунку трехмерная фигура восстанавливается неоднозначно. То есть в проекции заключена некоторая двусмысленность, недосказанность, которые и порождают «невозможный треугольник».

И можно сказать, что «невозможный треугольник» Пенроузов, как многие другие оптические иллюзии, стоит в одном ряду с логическими парадоксами и каламбурами.

Доказательство невозможности треугольника Пенроузов

Анализируя особенности двумерного изображения трехмерных объектов на плоскости, мы поняли, как особенности этого отображения приводят к невозможному треугольнику.

Доказать, что невозможный треугольник не существует, крайне легко, ведь каждый его угол прямой, а их сумма равна 270 вместо «положенных» 180.

Более того, даже если мы будем рассматривать невозможный треугольник, склеенный из уголков, меньших 90, то и в этом случае можно доказать, что невозможный треугольник не существует.

Рассмотрим ещё один треугольник, который состоит из нескольких частей. Если части, из которого он состоит, расположить по другому, то получится точно такой же треугольник, но с одним маленьким изъяном. Не будет хватать одного квадрата. Как такое возможно? Или все-таки это  иллюзия.

Использование феномена восприятия

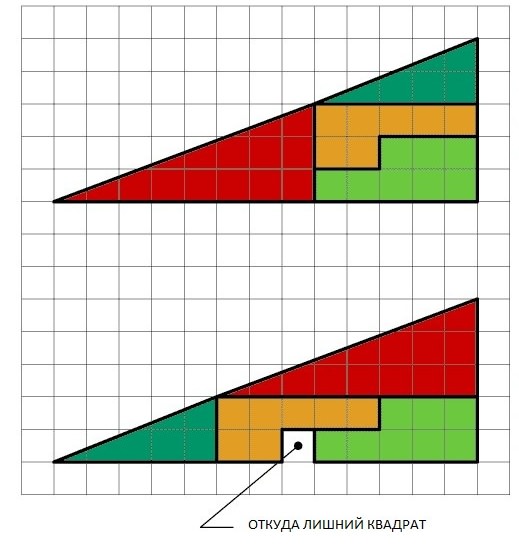
Можно ли как-нибудь усилить эффект невозможности? «Невозможнее» ли одни объекты, чем другие? И тут на помощь приходят особенности человеческого восприятия. Психологами установлено, что глаз начинает осмотр объекта (картины) с левого нижнего угла, затем взгляд скользит направо к центру и опускается в правый нижний угол картины. Такая траектория, возможно, связана с тем, что наши предки при встрече с противником сначала смотрели на самую опасную правую руку, а затем взгляд перемещался влево, на лицо и фигуру. Таким образом, художественное восприятие будет существенно зависеть от того, как строится композиция картины. Эта особенность в Средние века ярко проявилась при изготовлении гобеленов: их рисунок был зеркальным отражением оригинала, и впечатление, которое производят гобелены и оригиналы, различается.

Данное свойство можно с успехом использовать при создании творений с невозможными объектами, увеличивая или уменьшая «степень невозможности». Открывается также перспектива получать интересные композиции с использованием компьютерных технологий либо из нескольких картин, повернутых (может быть, с использованием различного вида симметрий) одна относительно другой, создающих у зрителей различное впечатление от объекта и более глубокое понимание сущности замысла, либо из одной, поворачивающейся (постоянно или рывками) при помощи нехитрого механизма на некоторые углы.

Такое направление можно назвать полигональным (многоугольным). На иллюстрациях представлены изображения, повернутые одно относительно другого. Композиция создавалась следующим образом: рисунок на бумаге, выполненный тушью и карандашом, сканировался, переводился в цифровую форму и обрабатывался в графическом редакторе. Можно отметить закономерность — повернутая картинка обладает большей «степенью невозможности», чем исходная. Это легко объяснимо: художник в процессе работы подсознательно стремится создать «правильное» изображение.

Заключение

Использование различных математических фигур и законов не ограничивается лишь вышеприведенными примерами. Внимательно изучая все приведенные фигуры, можно обнаружить и другие, не упомянутые в данной статье, геометрические тела или визуальную интерпретацию математических законов.

Математические изобразительное искусство процветает сегодня, и многие художники создают картины в стиле Эшера и в своем собственном стиле. Эти художники работают в различных направлениях, включая скульптуру, рисование на плоских и трехмерных поверхностях, литографию и компьютерную графику. А наиболее популярными темами математического искусства остаются многогранники, невозможные фигуры, ленты Мебиуса, искаженные системы перспективы и фракталы.

Выводы:

1. Итак, рассмотрение невозможных фигур развивают наше пространственное воображение, помогают «выйти» из плоскости в трехмерное пространство, что поможет при изучении стереометрии.

2. Модели невозможных фигур помогают рассматривать проекции на плоскости.

3. Рассмотрение математических софизмов и парадоксов прививают интерес к математике.

При выполнении данной работы

1. Я узнал — как, когда, где и кем была впервые рассмотрены невозможные фигуры, что таких фигур много, эти фигуры постоянно пытаются изображать художники.

2. Я, вместе с папой сделал модель невозможного треугольника, рассмотрел её проекции на плоскость, увидел парадокс данной фигуры.

3. Рассмотрел репродукции художников, на которых изображены данные фигуры

4. Мои исследования заинтересовали одноклассников.

В дальнейшем полученные знания я буду использовать на уроках математики и меня заинтересовали, а существуют ли другие парадоксы?

ЛИТЕРАТУРА

1. Кандидат технических наук Д. РАКОВ История невозможных фигур

2. Рутесвард О. Невозможные фигуры. — М.: Стройиздат, 1990.

3. Сайт В. Алексеева Невозможный треугольник Иллюзии · 7 Comments

4. Дж. Тимоти Анрах. – Удивительные фигуры.
   (ООО «Издательство АСТ», ООО «Издательство Астрель», 2002, 168 с.)

5. М. К. Эшер. – Графика.
   (Арт-Родник, 2001)

6. Даглас Хофштадтер. – Гедель, Эшер, Бах: эта бесконечная гирлянда.
   (Издательский дом «Бахрах-М», 2001)

7. А. Коненко – Тайны невозможных фигур
   (Омск:Левша, 199)