Тест по геометрии в 8 классе «Вписанная и описанная окружности»

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа №3»

г. Исилькуль, Омской области

Зинченко Елена Владимировна, учитель математики и информатики

Тест по теме «Вписанная и описанная окружности»

8 класс.

Цель данного теста – проверить уровень усвоения теоретического материала по данной теме.

Ключ к тесту:

I вариант 1б; 2а; 3в; 4в; 5б; 6в; 7а; 8б.

II вариант 1в; 2а; 3а; 4б; 5а; 6б; 7б; 8в.

Тест по теме «Вписанная и описанная окружности».

Вариант I.

1. Каждая точка биссектрисы неразвернутого угла равноудалена от его

а) углов; б) сторон; в) вершин.

2. Каждая точка серединного перпендикуляра к отрезку

а) равноудалена от концов этого отрезка;

б) равноудалена от середины этого отрезка;

в) равноудалена от углов.

3. Если все стороны многоугольника касаются окружности, то окружность называется

а) описанной около многоугольника;

б) вписанной в треугольник;

в) вписанной в многоугольник.

4. В любой треугольник можно вписать только

а) две окружности;

б) три окружности

в) одну окружность.

5. В любом вписанном четырехугольнике сумма противолежащих углов равна

а) 360; б) 180; в) 90.

6. Центр вписанной окружности лежит в точке пересечения

а) медиан;

б) серединных перпендикуляров;

в) биссектрис.

7. Описанная около треугольника окружность изображена на рисунке:

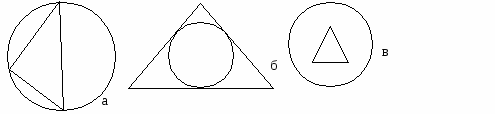
8. Вписанная в четырехугольник окружность изображена на рисунке:

Тест по теме «Вписанная и описанная окружности».

Вариант II.

1. Каждая точка, равноудаленная от сторон угла, лежит на его

а) медиане; б) высоте; в) биссектрисе.

2. Серединным перпендикуляром к отрезку называется прямая,

а) проходящая через середину данного отрезка и перпендикулярная к нему;

б) проходящая через середину данного отрезка;

в) перпендикулярная к отрезку.

3. Если все вершины многоугольника лежат на окружности, то окружность называется

а) описанной около многоугольника;

б) описанной около треугольника;

в) вписанной в многоугольник.

4. Около любого треугольника можно описать только

а) две окружности;

б) одну окружность;

в) три окружности.

5. В любом описанном четырехугольнике суммы противолежащих сторон

а) равны; б) равны радиусу; в) равны периметру.

6. Центр описанной окружности лежит в точке пересечения

а) медиан;

б) серединных перпендикуляров;

в) биссектрис.

7. Вписанная в треугольник окружность изображена на рисунке:

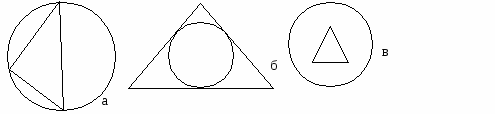
8. Описанная около четырехугольника окружность изображена на рисунке:

Литература.

1. Л.С. Атанасян, В.Ф. Бутузов и др. «Геометрия 7-9», учебник для общеобразовательных учреждений, Москва, «Просвещение», 2012 г.

2. Н.Ф. Гаврилова «Поурочные разработки по геометрии 8 класс», Москва, «ВАКО», 2006 г.