Конспект урока на тему «Вычитание многозначных чисел. Алгоритм действий»

Настрой на урок. Проверка рабочих мест и посадки детей.

Девиз урока: «То, что мы усвоили, не забудем никогда»

— Урок математики.

— Как называется тема, над которой мы работали последние уроки? (Сложение многозначных чисел)

— Кто из вас считает, что освоил эту тему хорошо и разобрался во всех особенностях сложения многозначных чисел, достиг успеха? (Поднимают руку)

— Кто считает, что в сложении многозначных чисел еще остались трудности?

— Контрольная работа показала, что вы все с успехом справляетесь с данной темой.

— Что необходимо помнить для успешного выполнения сложения? (алгоритм)

• Поработаем в группах. Необходимо записать алгоритм выполнения сложения многозначных чисел. (На листах для каждой группы запись алгоритма с пропусками):

1. Поставить ________________ и показать, какие _____________ переполняются.

Узнать, сколько _____________ будет в сумме.

Определить цифру в каждом ____________.

— Предлагаю мастер-класс. От каждого ряда по 3 человека на выполнение 3-х шагов алгоритма и по 3 человека на решение выражения. Выполнить письменный приём сложения многозначных чисел.

(На доске в столбик записаны выражения для 2-х команд-рядов):

434₅ + 321₅

245₆ + 532₆

422₇ + 521₇

Подведение итога.

— А в какой системе вам легче выполнять сложение? (в десятичной)

— Какие же могут быть ошибки при нахождении суммы?

1. Ошибка в записи.

Как это показать графически? (Заранее заготовлены разные модели, дети выбирают подходящую)

— Записывать нужно поразрядно!

2. Не определили переполнение разрядов.

3. Не прибавили единицу.

— На экране схема №1. Составьте выражение по данной схеме.

6718 3622

X

+

(Учащиеся выполняют решение по отработанному алгоритму).

2. Ситуация неуспеха (разрыва).

— Схема №2. Выполнить аналогичную работу.

X 3622

6718

(Выясняется, что найти неизвестное учащиеся не могут, т.к. необходимо выполнить вычитание)

3. Контроль способа.

— Еще раз скажем, что выполнять сложение мы в данном случае не можем, т.к. нам необходимо найти часть целого, а часть находится вычитанием. Т.е. изученный способ не подходит.

4. Перевод частной проблемы в общую.

— Чего мы не знаем для решения данной проблемы?

(Как выполнить вычитание, т.е. алгоритм)

5. Постановка учебной задачи (мотивация)

— Какова же будет учебная задача урока? (Познакомиться с алгоритмом вычитания многозначных чисел)

6. Решение учебной задачи.

На доске модель.

— Даны величины А и В. Назовите величины числом. (246 и 182).

— Какая величина больше и на сколько?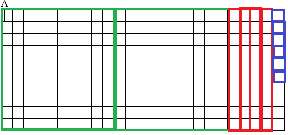

В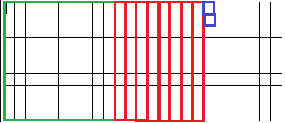

Величина А Величина В

E _{3 =} 2 Е ₃ = 1

E ₂ = 4 Е ₂ = 8

E ₁ = 6 Е ₁ = 2

— Как нам поступить?

— Какие могут быть предположения ваших действий? (дети выдвигают гипотезы)

— Предлагаю вам поработать в группах и найти путь решения проблемы.

На столах у детей заготовки-модели величин, ножницы, карандаши. Учащиеся работают, высказывают предположения. Далее идет отчет групп. Оформление общего результата работы.

7. Обобщение знаний. Моделирование.

— На какие вопросы мы должны будем отвечать, чтобы научиться вычитать многозначные числа? (т.е. алгоритм) Сначала выслушать детей. Затем попросить восстановить алгоритм:

1. Определить, какие разряды («разбиваются») и поставить стрелки.

2. Определить, сколько (цифр) будет в результате и сделать заготовку.

3. Определить цифру в каждом (разряде).

—

Первичное закрепление.

Вычисления выполняют столбиком в тетради (сколько успеют)

603 – 196 539 — 436

1612 – 534 602 — 540

4270 – 809 478 — 32

8027 – 768 577 — 328

9. Рефлексия

— Подтвердилась ли ваша гипотеза?

— Есть ли среди нас человек, которому все, о чем мы сегодня говорили, было недоступно?

— Есть ли человек среди вас, которому было сегодня скучно?

— Есть ли тот, кто все уже и до урока знал?

— Кому-нибудь это показалось бесполезным?

— Стало ли проблем больше/меньше?

— Определим задачу на следующий урок.