Разработка урока математики на тему: «Последовательности. Способызадания и свойства числовых последовательностей» 10-11 класс

Областное государственное бюджетное образовательное учреждение среднего профессионального образования

«Белгородский строительный колледж»

Разработка занятия по дисциплине «Математика»

для студентов СПО 1 курса

(применима для 10-11 класса общеобразовательной школы)

по теме:

Последовательности. Способы задания и свойства числовых последовательностей.

Подготовила:

преподаватель математики и информатики БСК

Кобзева Ирина Алексеевна

Белгород

2013 г.

Тема: Последовательности. Способы задания и свойства числовых последовательностей.

Цели:

Обучающая: дать понятие и определение числовой последовательности, рассмотреть способы задания числовых последовательностей, решать упражнения.

Развивающая: развивать логическое мышление, познавательные навыки, техники вычисления, навыки сравнения при выборе формул, навыки учебного труда

Воспитательная: воспитание положительных мотивов к учебе, добросовестного отношения к труду, дисциплинированности.

Тип занятия: комбинированный урок.

Оборудование: интерактивная доска, раздаточный материал, презентация.

План урока

1. Орг. момент.

2. Изучение нового материала.

3. Закрепление.

4. Подведение итогов.

Ход урока

I. Организационный момент.

Отметить отсутствующих, сообщить студентам цели и задачи занятия.

В 9 классе на уроках алгебры вы уже встречались с понятием числовой последовательности. Рассматривали свойства некоторых последовательностей, способы их задания. Арифметическая и геометрическая прогрессии нами были изучены более подробно. Вы познакомились с формулами n-го члена прогрессии, суммы n первых членов прогрессии. Настало время вспомнить и обобщить изученный материал, систематизировать его и применить к более сложным понятиям. На последующих занятиях нам предстоит рассмотреть одну из важнейших тем математического анализа – «Пределы». Сегодняшнее занятие будет подготовкой к изучению этой темы, т.е. фундаментом, на котором потом выстроится здание с названием «Предел».

II. Изучение нового материала.

Обратимся к следующим примерам числовых последовательностей:

1, 2, 4, 8, 16, 32, 64, 128, …                                (1)     

5, 7, 9, 11, 13, 15, 17, 19, …                                (2)

1, 4, 9, 16, 25, 36, 49, 64, …                                (3)

1,  √2,  √3, 2,  √5,  √6,  √7,  2√2, …                    (4)   

                                  (5)   

2, 0, -2, -4, -6, -8, -10, -12, …                                (6)    

                                (7)    

                                        (8)

                                (9)    

                             (10)

Внимательно посмотрите на эти примеры. Что у них общего? В каждом примере выписано по восемь членов последовательности. Могли бы вы написать, например, девятые члены?

Значит, во всех приведенных примеров последовательностей налицо определенный закон, который позволяет нам дописать девятые, десятые и прочие члены последовательностей. Правда, надо заметить, что задание некоторого конечного числа членов может и не выявить закона, по которому построена бесконечная последовательность.

В данном случае эти законы хорошо просматриваются. В примере (1) перед нами члены бесконечной геометрической прогрессии со знаменателем 2. В примере (2) имеем последовательно расположенные нечетные числа, начиная с 5. В примере (3) последовательно расположенные квадраты натуральных чисел…

Будем рассуждать более строго. Пронумеруем все члены последовательности по порядку: 1, 2, 3, …, n, …

Существует некий закон (некое правило), по которому каждому из этих натуральных чисел ставится в соответствие определенное число (соответствующий член последовательности). В примере (1) это соответствие выглядит так:

          (члены последовательности)

1  2  3  4  5    6   …  n …             (номера мест)

Для задания последовательности достаточно указать, какой член последовательности соответствует числу n, т.е. стоит на n-ом месте. Можно сформулировать следующее определение последовательности.

Говорят, что задана числовая последовательность, если всякому натуральному числу (номеру места) по какому-либо закону однозначно поставлено в соответствие определенное число (член последовательности).

В общем виде указанное соответствие можно изобразить так: 

1    2     3     4    5 … n …  

Число есть n-ый член последовательности. Всю последовательность обычно обозначают .

Возвращаясь к нашим примерам последовательностей, рассмотрим в каждом случае аналитическое выражение (формулу) для n-го члена.

В примере (1) имеем . В примере (2): . В примере (3): .В примере (4): . В примере (5): . В примере (6): . В примере (7):. В примере (8):   если п = 2к ; и , если п = 2к — 1. Важно заметить, что способ задания последовательности при помощи формулы для её n-го члена не является единственным.
Наряду со способом, рассмотренным выше, применяют рекуррентное (латинское слово recurrere – «возвращаться») задание последовательности. В этом случае для задания последовательности надо указать первый (или несколько первых) член последовательности и рекуррентное соотношение, выражающее n-ый член последовательности через предыдущий (или несколько предыдущих).

Используя рекуррентный способ, представим последовательность (1) так: . Последовательность (2):

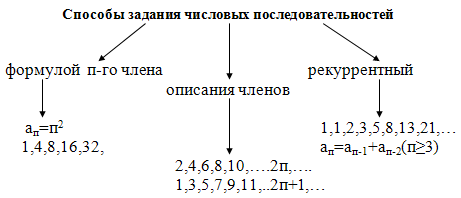
Пользуясь рекуррентным способом, определим одну любопытную последовательность:. Вот ее первые члены:

1, 1, 2, 3, 5, 8, 13, 21, …           (11)  

Она известна как последовательность чисел Фибоначчи.

Может быть, кто-то из вас слышал о задаче с кроликами Фибоначчи. От этой задачи, сформулированной итальянским математиком  XIII века Фибоначчи, и происходит название последовательности. Задача такова:

Некто поместил пару новорожденных кроликов в огороженный загон и хочет знать, сколько кроликов у него будет через некоторое время. Условия задачи таковы: пара кроликов начинает давать потомство через два месяца после своего рождения, и каждый месяц появляется одна пара кроликов. В начале (в первом месяце) мы имеем в загоне одну пару кроликов (у₁ = 1), во втором месяце имеем по прежнему одну пару (у₂ = 1), в третьем месяце появляется приплод, поэтому число пар кроликов в загоне становится равным двум (у₃ = 2), в четвертом месяце появляется еще один приплод от первой пары кроликов (у₄ = 3), в пятом месяце появляется приплод как от первой, так и от второй пар кроликов (у₅ = 5) и т.д.

Увеличение пар кроликов в загоне от месяца к месяцу хорошо иллюстрирует рисунок. Можно видеть, что число пар кроликов подсчитываемые каждый месяц образуют последовательность (11), т.е. последовательность чисел Фибоначчи.

Последовательность чисел Фибоначчи любопытна вовсе не потому, что описывает упрощенную схему размножения кроликов. Оказывается, что эта последовательность загадочным образом возникает в самых неожиданных ситуациях. Например, в настоящее время числа Фибоначчи применяются при обработке информации с помощью ЭВМ, при поиске оптимальных методов программирования. Впрочем, это уже отдельная тема для разговора.

Свойства

Определение:

Последовательность (у_n), называют ограниченной сверху, если все ее члены не больше некоторого числа.

Последовательность (у_n) ограничена сверху, если существует число М такое, что для любого n выполняется неравенство уn ≤ М. Число М называют верхней границей последовательности.

Например: -1, -4, -9, -16,…, — n² ,…

Верхняя граница: -1

Определение:

Последовательность (у_n), называют ограниченной снизу, если все ее члены не меньше некоторого числа.

Последовательность (у_n) ограничена снизу, если существует число m такое, что для любого n выполняется неравенство у_n ≥ m. Число m называют верхней границей последовательности.

Например: 1, 4, 9, 16,…,n²,…

Нижняя граница: 1

Если последовательность ограничена и снизу и сверху, то ее называют ограниченной последовательностью.

Ограниченность последовательности означает, что все члены последовательности принадлежат некоторому отрезку.

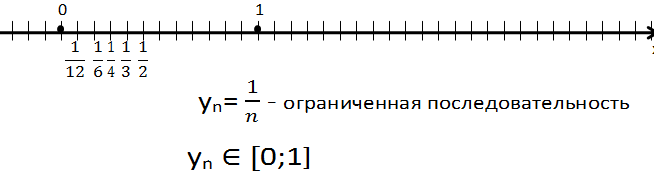III. Закрепление.

1. Выполнить задания со слайда.

Продолжите ряд: 1, 10, 3, 9, 5, 8, 7, 7, 9, 6…

Ответ: Ряд состоит из двух частей: числа на нечетных местах: 1, 3, 5, 7, 9…; числа на четных местах: 10, 9, 8, 7

Продолжите ряд 77, 49, 36, 18…

Ответ: Перемножаются две цифры, входящие в предыдущее число.

2) Напишите первые пять членов последовательности.

1. а_n=2ⁿ+1/2ⁿ

2. х_n=3n²+2n+1

1. Решение:

а_n=2ⁿ+1/2ⁿ

Ответ:

2. Решение:

X_n=3n²+2n+1

n=1, x₁=3*1²+2*1+1=3+2+1=6

n=2, x₂=3*2²+2*2+1=3*4+4+1=12+5=17

n=3, x₃=3*3²+2*3+1=27+6+1=34

n=4, x₄=3*4²+2-4+1=3*16+8+1=48+9=57

n=5, x₅=3*5²+2*5+1=3*25+10+1=75+11=86

Ответ: 6,17,34,57,86…….

3). Напишите формулу общего члена последовательности натуральных чисел, кратных 3.

Ответ: 0,3,6,9,12,15,…. 3n, а_n =3n

4). Напишите формулу общего члена последовательности натуральных чисел, кратных 7.

Ответ: 0,7,14,25,28,35,42…. 7n, а_n =7n

5). Напишите формулу общего члена последовательности натуральных чисел, которые при делении на 4 дают в остатке 1.

Ответ:5,9,13,17,21……. 4_n +1 , а_n =4n+1

6). Напишите формулу общего члена последовательности натуральных чисел, которые при делении на 5 дают в остатке 2.

Ответ: а_n =5n+2, 7.12,17,22, 27,…. 5_n +2

7). Напишите формулу общего члена последовательности.

1) 5,9,13,17,……

Ответ: а_n =4n+1

2)

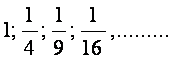
Решение:

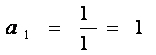
Ответ:

8) Фронтальный опрос.

1. Что называется числовой последовательностью?

Ответ: Множество чисел, элементы которого можно пронумеровать.

2. Приведи пример числовой последовательности.

Ответ:

2,4,6,8,10,…..
1,3,5,7,9,11,…..
3,6,9,12,15,….

3. Что называется членами числовой последовательности?

Ответ: Числа, составляющие числовую последовательность.

а₁=2,а₂=4,а₃=6,а₄=8,….
а₁=1,а₂=3,а₃=5,а₄=7,….
а₁=3,а₂=6,а₃=9,а₄=12,….

4. Что такое общий член числовой последовательности?

Ответ: а_n называется общим членом последовательности ,а саму последовательность коротко обозначают через {а_n}.

5. Как обозначают числовую последовательность?

Ответ: Обычно числовую последовательность обозначают малыми буквами латинского алфавита с индексами, указывающими на номер этого члена в последовательности: а₁,а₂,а₃,а₄,….,а_n,…

IV. Подведение итогов.

Выставление оценок.