Модули. ЕГЭ.
Автор – Прокофьева Тамара Александровна,
учитель МБОУ СОШ №12 г. Дзержинска Нижегородской обл.
Тема «Абсолютная величина» включена в список тем, проверяемых на ЕГЭ 2013.
Тему «Модули» можно углубленно изучать в средней школе:
во время предпрофильной подготовки в 8-9 классах в рамках элективного курса «Модуль» — 8 часов, автор Студенецкая В.Н.;
во время изучения элективного курса «Алгебра +», автор Земляков А.Н. учащиеся работают с темами «Уравнения с модулями. Раскрытие модулей — стандартные схемы. Метод интервалов при раскрытии модулей. Неравенства с модулями. Схемы освобождения от модулей в неравенствах. Эквивалентные замены разностей модулей в разложенных и дробных неравенствах («правило знаков»). Задачи с модулями и параметром»;
во время непрерывного повторения;
на уроках итогового повторения и обобщения.
Правила решений.
Уравнения:
1) ![]() , где
, где ![]()
![]()
![]()
2)![]()
1 способ. По определению модуля данное уравнение равносильно совокупности двух систем:
1) 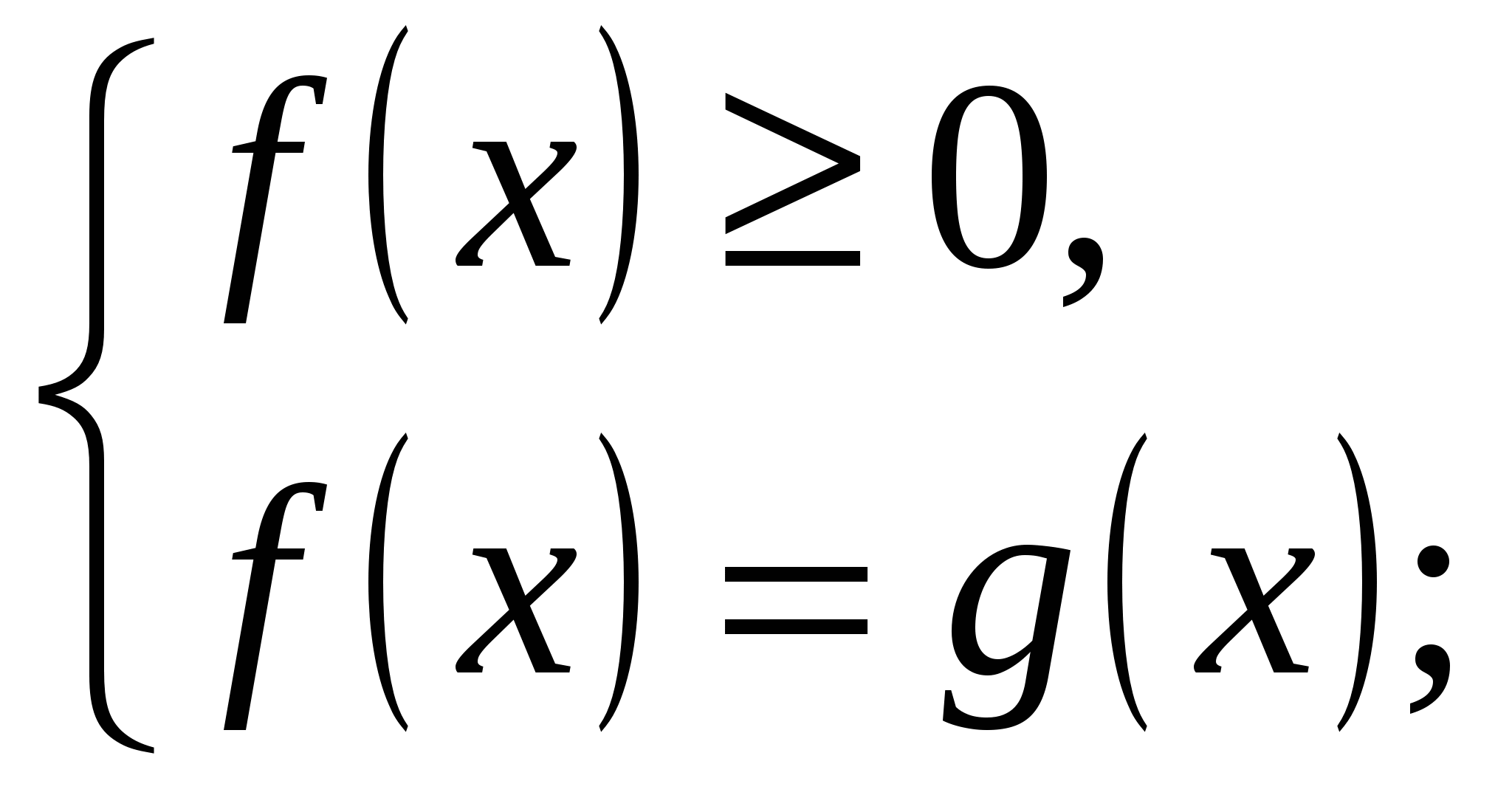 2)
2) 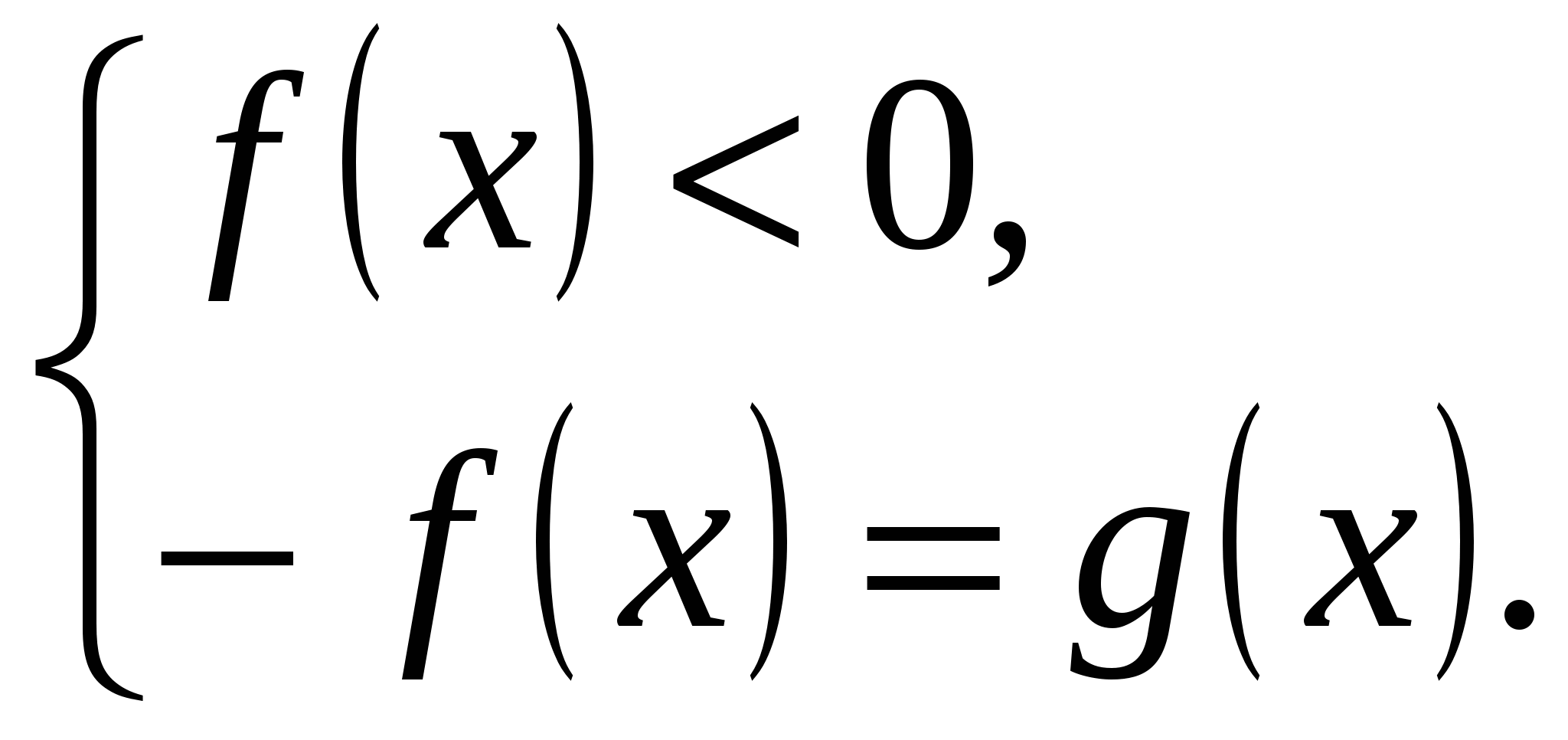 «раскрытие модуля изнутри»;
«раскрытие модуля изнутри»;
2 способ. По свойству модуля данное уравнение равносильно совокупности двух систем:
1) 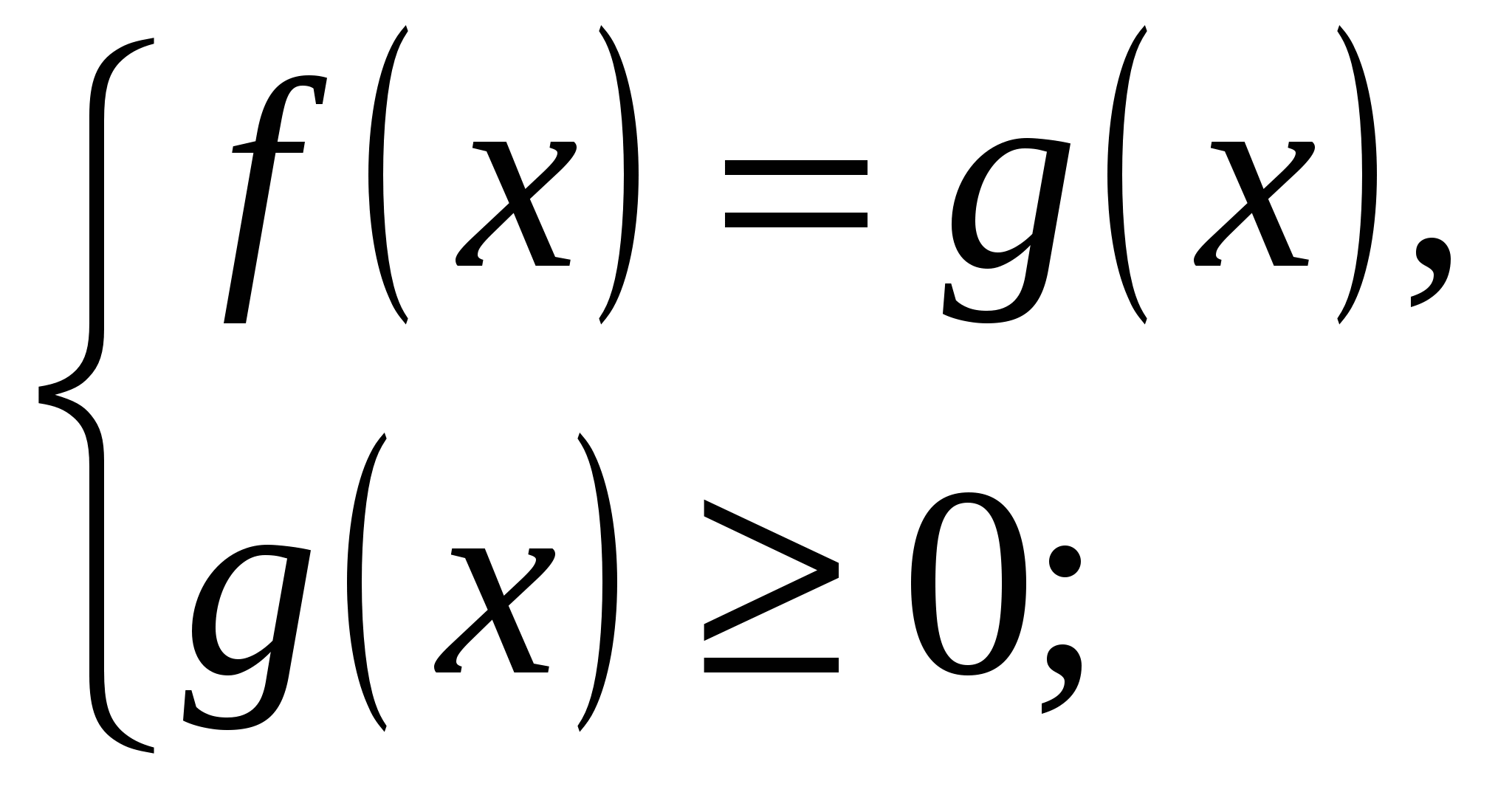 2)
2) 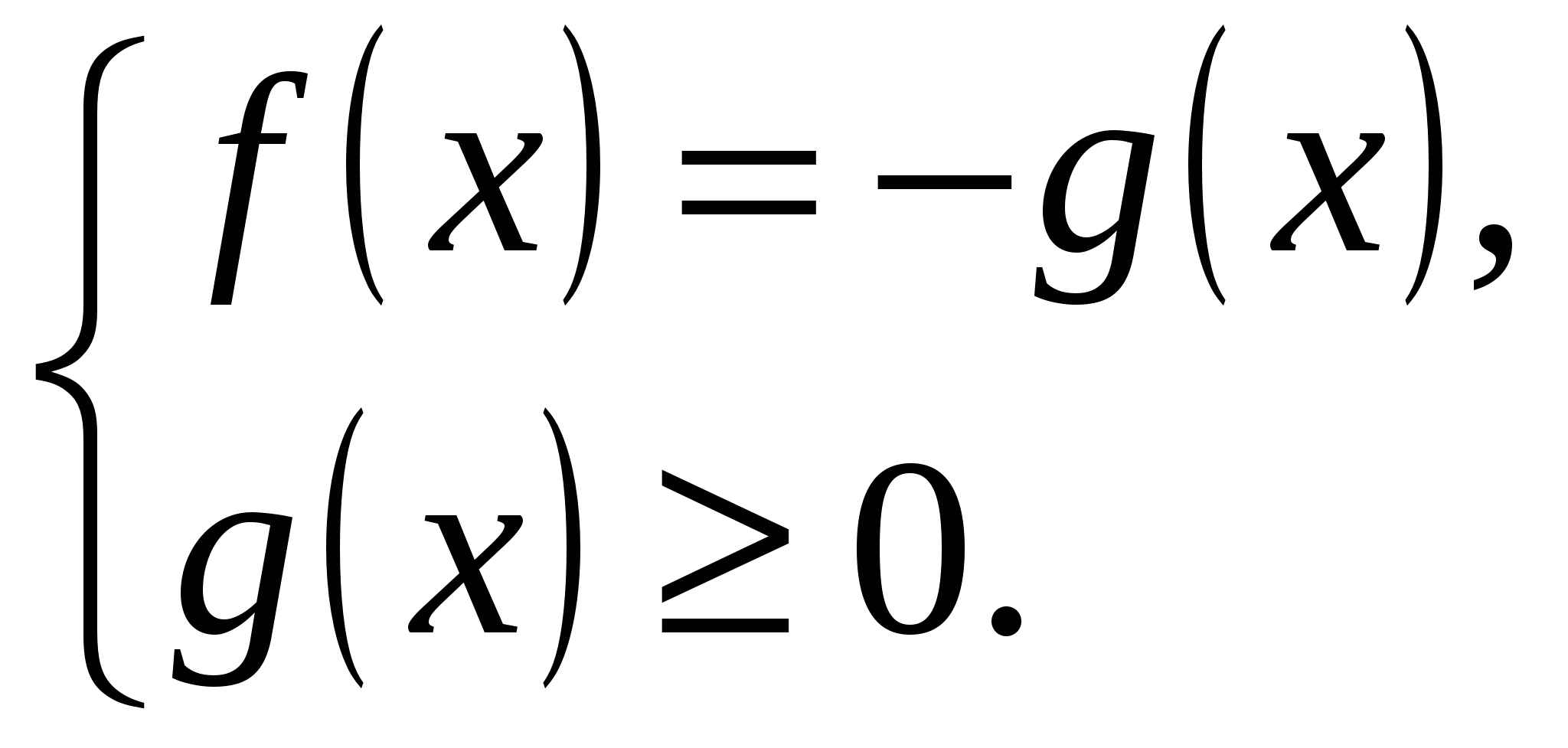 «раскрытие модуля снаружи»;
«раскрытие модуля снаружи»;
3) ![]()
![]()
![]()
4) ![]()
![]()
![]() .
.
Неравенства:
1) ![]() , если
, если ![]() , то
, то ![]() .
.
2) ![]() , где
, где ![]()
![]()
![]() .
.
3) ![]() .
.
1 способ. По определению модуля данное неравенство равносильно совокупности систем неравенств: а) 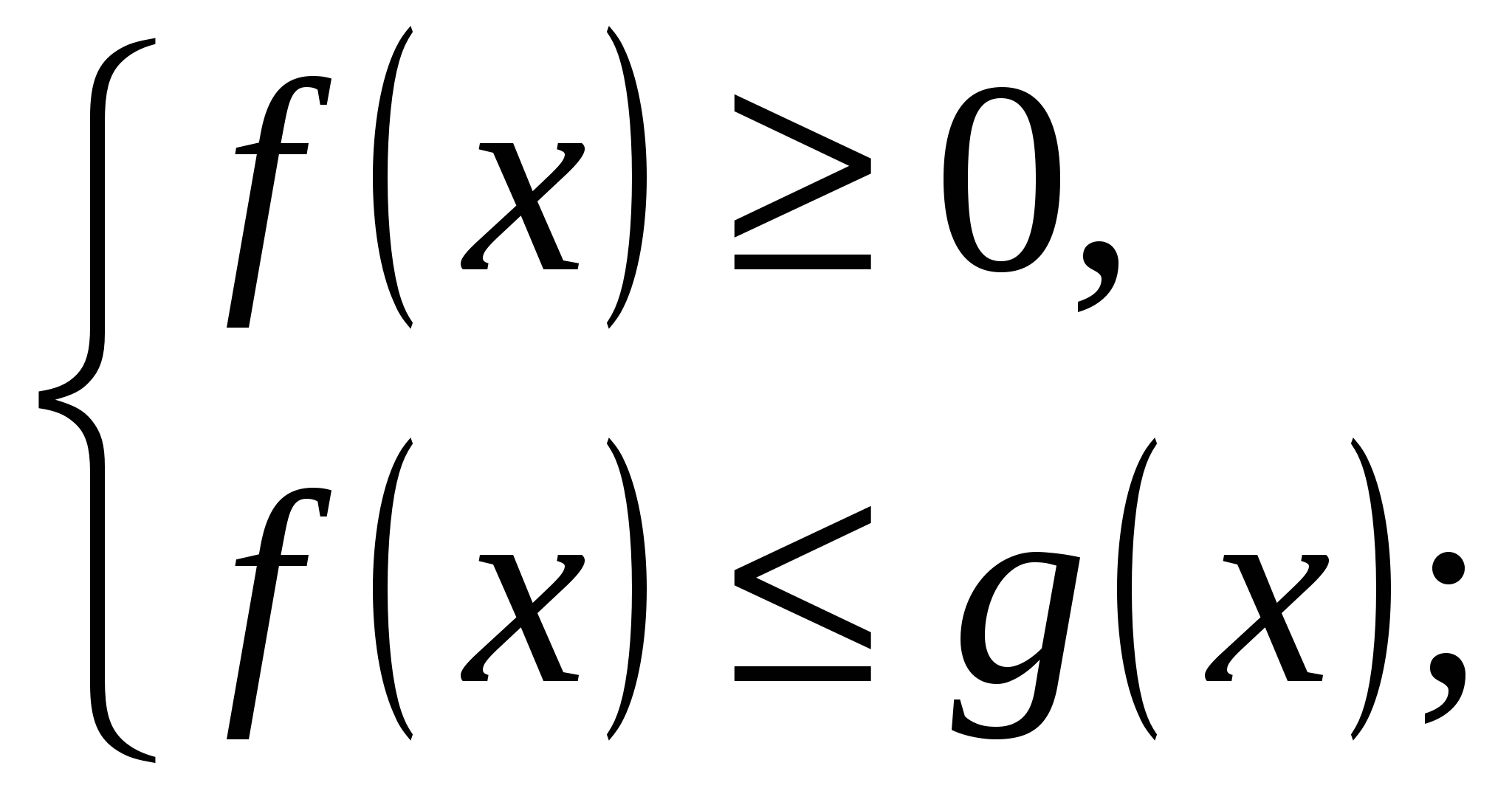 б)
б) 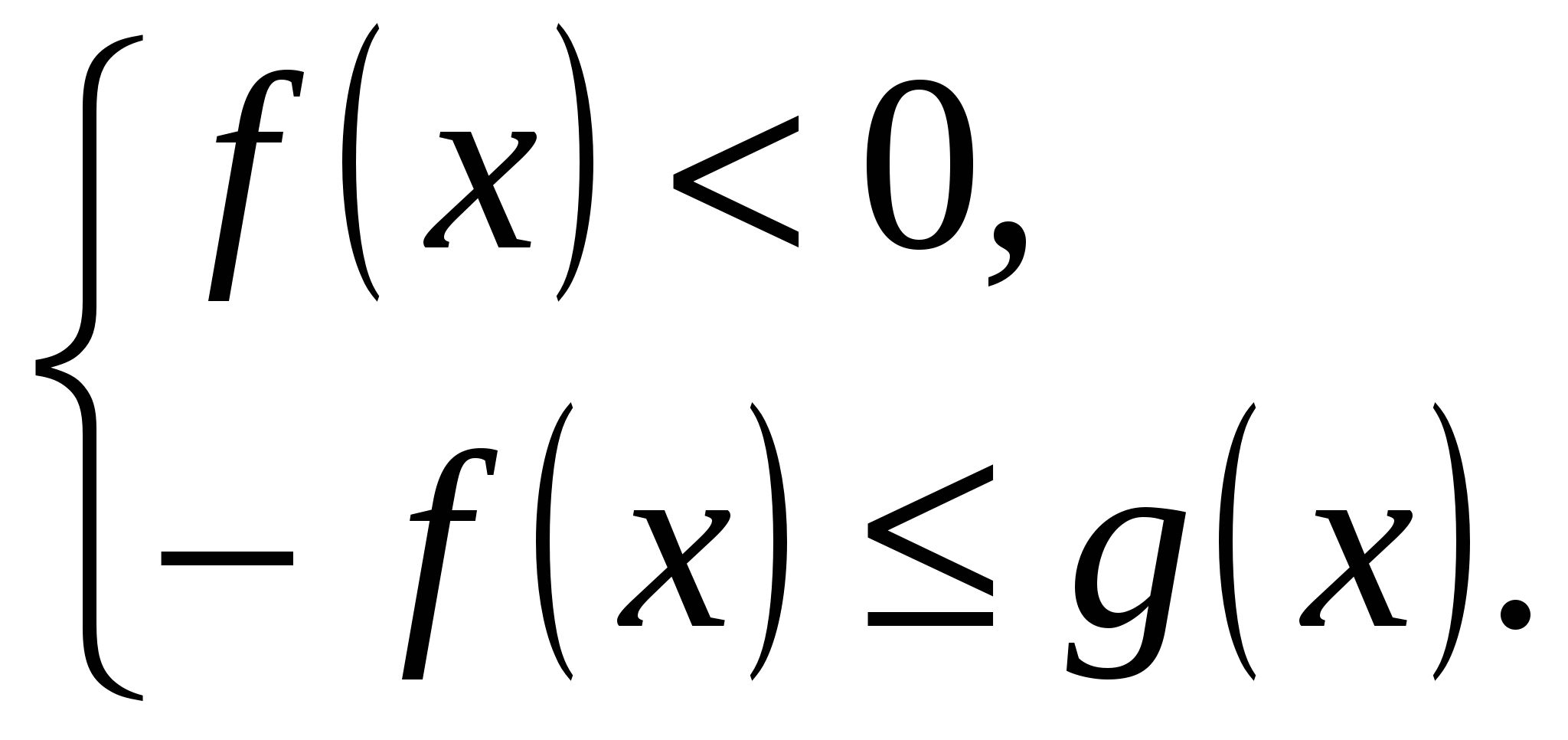 Это «раскрытие модуля изнутри».
Это «раскрытие модуля изнутри».
2 способ. По свойству модуля от неравенства ![]() переходим к системе неравенств
переходим к системе неравенств 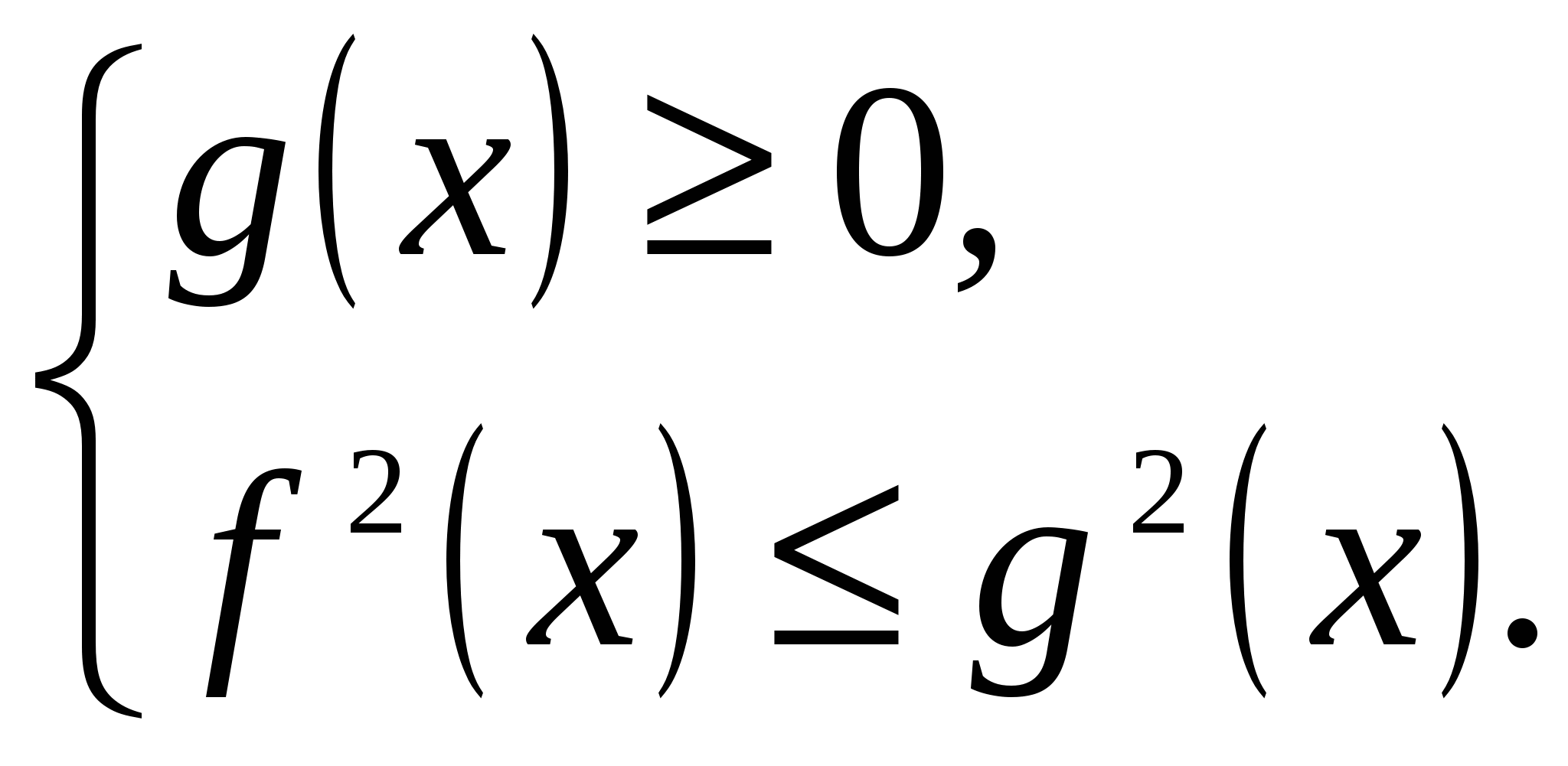
3 способ. «Раскрытие модуля снаружи».
![]()
![]()
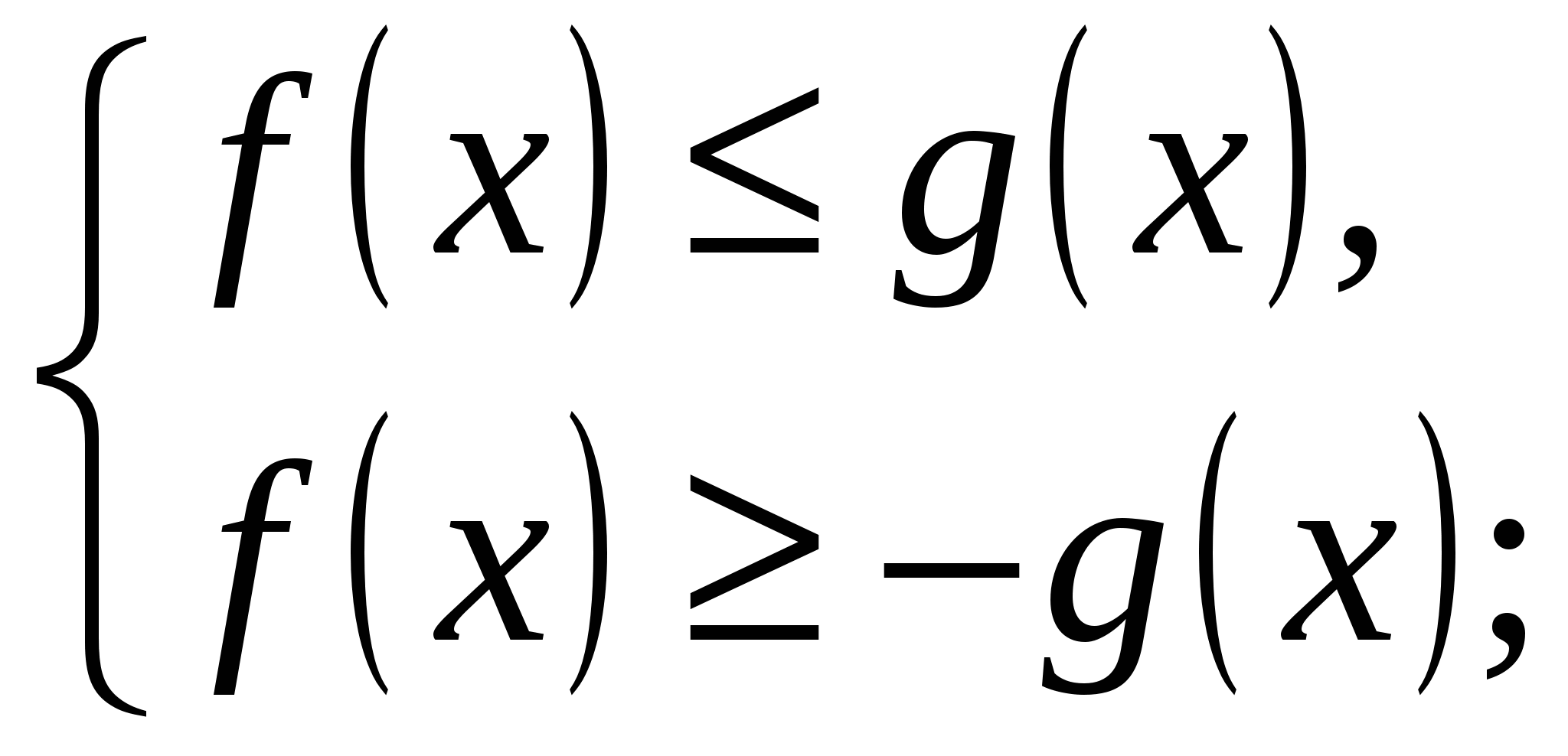
![]()
![]() .
.
4) ![]()
![]()
![]()
5) ![]()
![]()
![]() .
.
6) ![]()
![]()
![]() .
.
Особые свойства модуля:
1) ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() ,
,
2) ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() и
и ![]() ,
,
3) ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() .
.
Выражения, содержащие модули.
1) Найти целое число, равное разности ![]() .
.
Решение.
Сравним числа ![]() и
и ![]() . Возведем их в квадрат
. Возведем их в квадрат ![]() ,
, ![]() , тогда
, тогда
![]() и
и ![]() ,
, ![]() .
.
![]() =
= ![]() ,
, ![]() .
.
1 способ.
Преобразуем подкоренные выражения:
![]() ,
,
![]() .
.
![]() .
.
2 способ.
Возведем равенство в квадрат:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() т. к.
т. к. ![]() , то
, то ![]() .
.
Ответ. -10
2) Упростить выражение ![]() при
при ![]() .
.
Решение.
![]()
![]() =
=![]()
![]() .
.
![]() , тогда
, тогда ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
![]() .
.
Ответ.10
3) Упростить выражение ![]() при всех допустимых значениях переменной.
при всех допустимых значениях переменной.
Решение.
Пусть ![]() =
=![]() , тогда
, тогда
![]() .
.
Найдем нули подмодульных выражений:
![]()
![]()
Найденные значения ![]() разбивают числовую ось на три числовых промежутка.
разбивают числовую ось на три числовых промежутка.
Определим знаки подмодульных выражений на этих числовых промежутках:
|
|
|
| |
|
| — | — | + |
|
| — | + | + |
а) если ![]() , то
, то ![]() ,
,
б) если ![]() , то
, то ![]() ,
,
в) если ![]() , то
, то ![]()
![]() .
.
Ответ. ![]() , если
, если ![]() ;
; ![]() , если
, если ![]() ;
; ![]() , если
, если ![]() .
.
Уравнения с модулями.
1) Решите уравнение ![]() . В ответе укажите наименьший положительный корень (в градусах).
. В ответе укажите наименьший положительный корень (в градусах).
Решение.
Модуль, равный 3 имеют два числа, поэтому рассмотрим два случая:
а) ![]() , б)
, б) ![]() ,
,
![]() ,
, ![]() ,
,
корней нет; ![]() — наименьший положит. корень.
— наименьший положит. корень.
Ответ. 270
2) Решите уравнение ![]() . (Если уравнение имеет более одного корня, то в бланке ответов запишите сумму всех его корней.)
. (Если уравнение имеет более одного корня, то в бланке ответов запишите сумму всех его корней.)
Решение.
Рассмотрим способ «раскрытия модуля снаружи». Данное уравнение равносильно совокупности двух систем:
а)  б)
б) 
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
корней нет при ![]() ;
; ![]() удовлетворяет условиям системы.
удовлетворяет условиям системы.
Ответ. 0
3) Решите уравнение ![]() . В ответе укажите наименьший положительный корень (в градусах).
. В ответе укажите наименьший положительный корень (в градусах).
Решение.
Раскроем модуль по определению. Этот способ называется «раскрытие модуля изнутри».
Данное уравнение равносильно совокупности двух систем:
а) 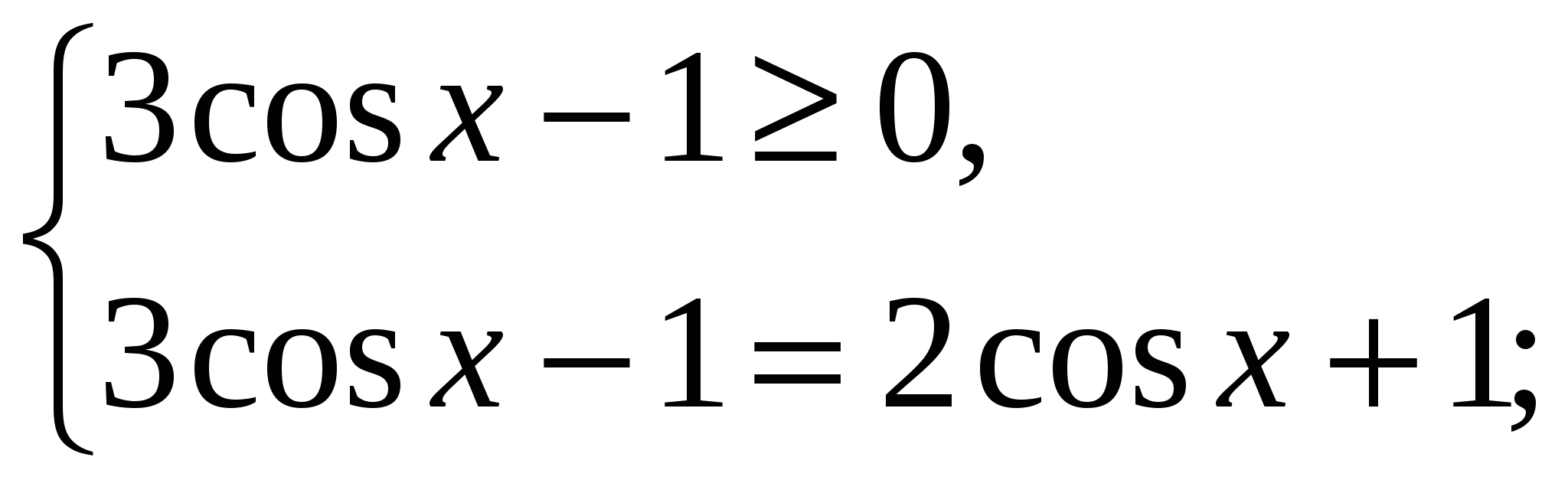 б)
б) 
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
корней нет при ![]() ;
; ![]() ,
,
![]()
![]() ;
;

![]() .
.
![]() — наибольший отрицательный корень.
— наибольший отрицательный корень.
Ответ. -90
4) Укажите наибольшее решение уравнения ![]() .
.
Решение.
Область определения уравнения ![]() .
.
Перепишем уравнение в другом виде: ![]() .
.
По определению модуля: ![]() при
при ![]() ,
,
тогда данное уравнение равносильно условию:
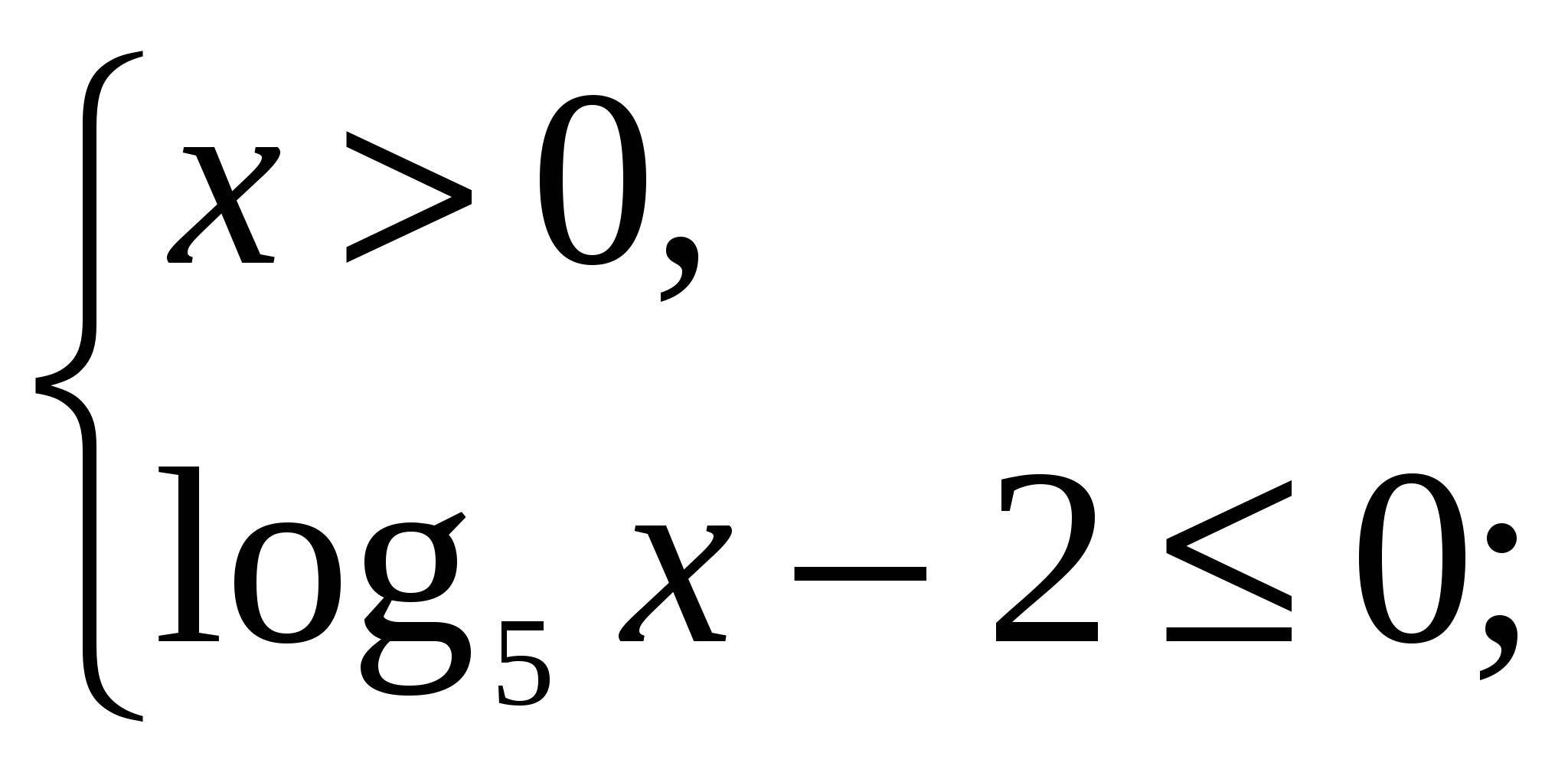
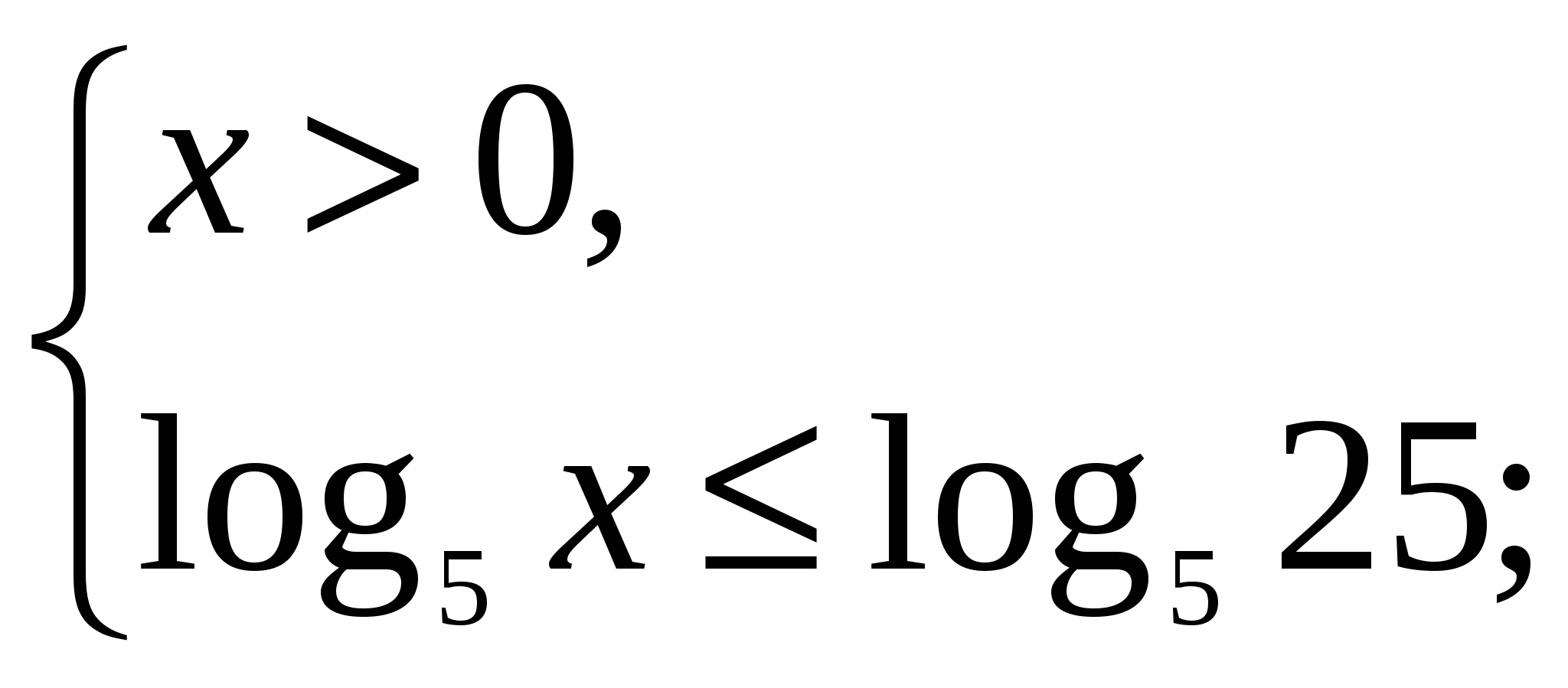
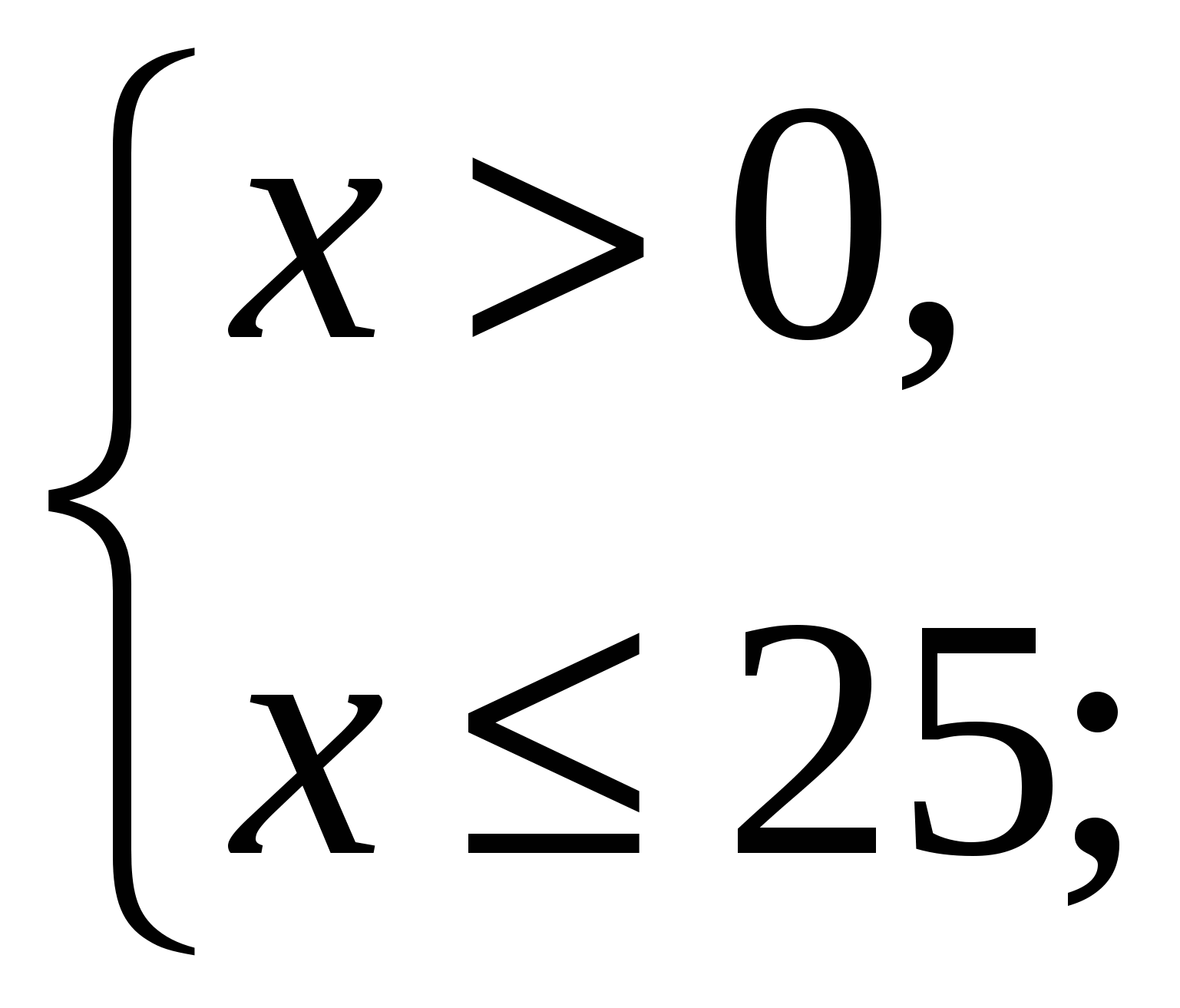
![]() ;
;
![]() — наибольшее решение уравнения.
— наибольшее решение уравнения.
Ответ. 25
5) Решите уравнение ![]() . (Если уравнение имеет более одного корня, то в бланке ответов запишите произведение всех его корней.)
. (Если уравнение имеет более одного корня, то в бланке ответов запишите произведение всех его корней.)
Решение.
Данное уравнение равносильно совокупности двух уравнений:
а) ![]() , б)
, б) ![]() ,
,
![]() ,
, ![]() ,
,
корней нет; ![]() ,
, ![]() .
.
Ответ. 2
6) Решите уравнение ![]() .
.
Решение.
Область определения уравнения: ![]() .
.
Рассмотрим решение уравнения методом интервалов.
Найдем нули подмодульных выражений:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Полученные значения разбивают область определения уравнения на три числовых промежутка. Определим знаки подмодульных выражений на полученных промежутках:
|
|
|
| |
|
| — | + | + |
|
| — | — | + |
1) 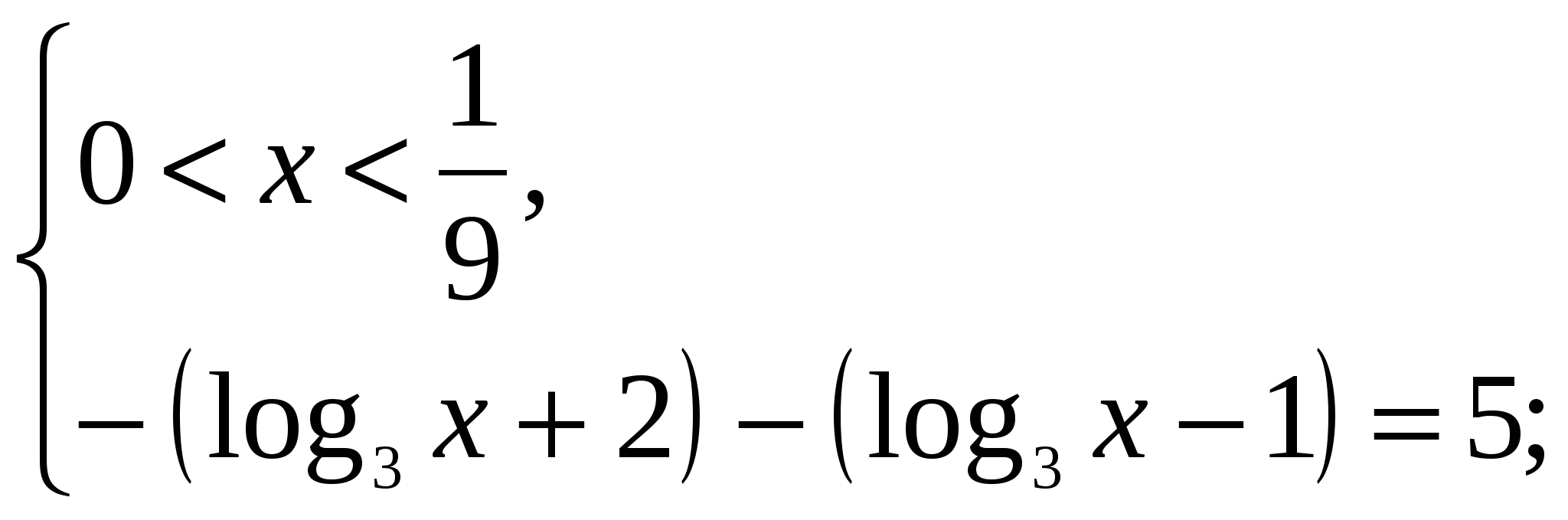
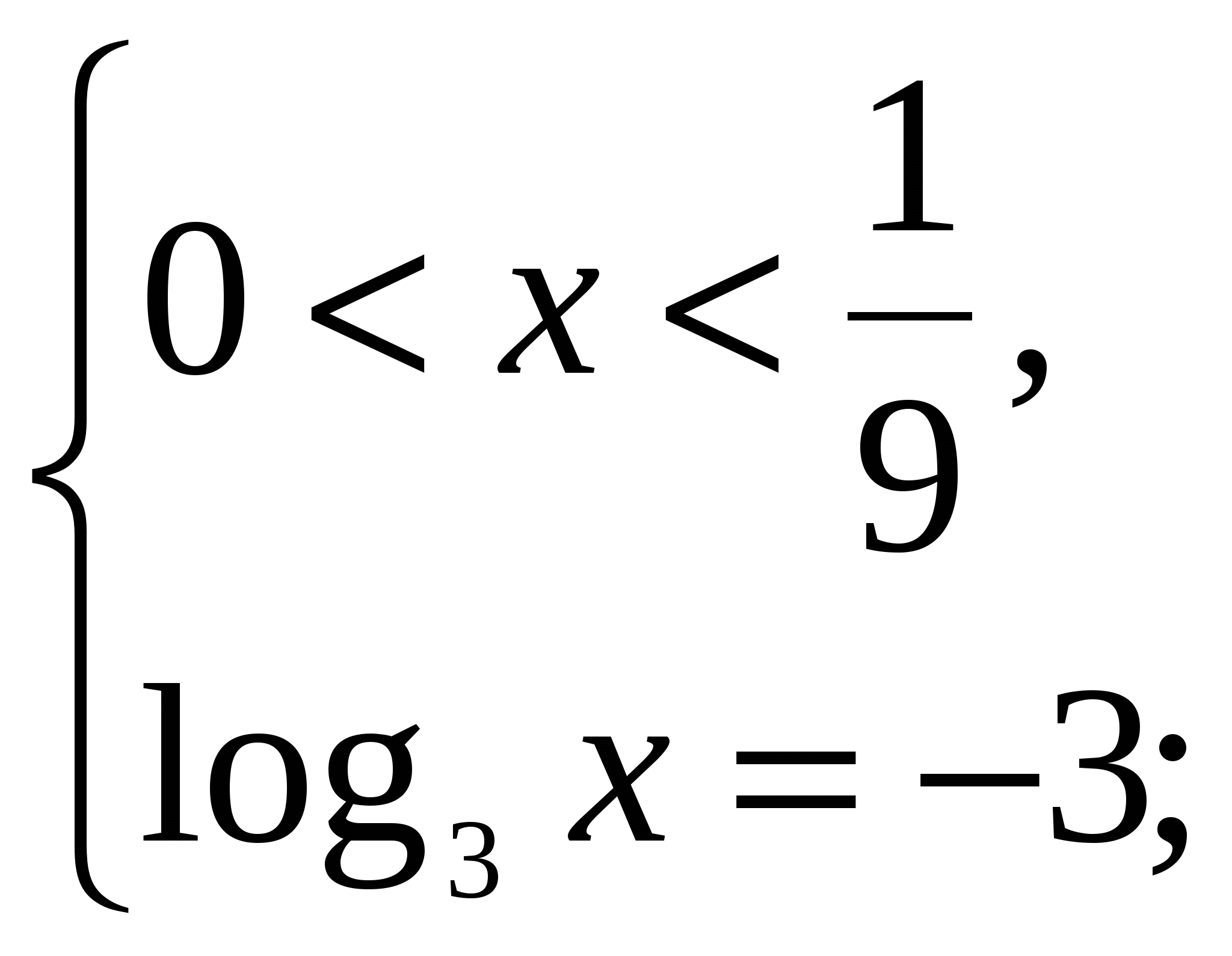
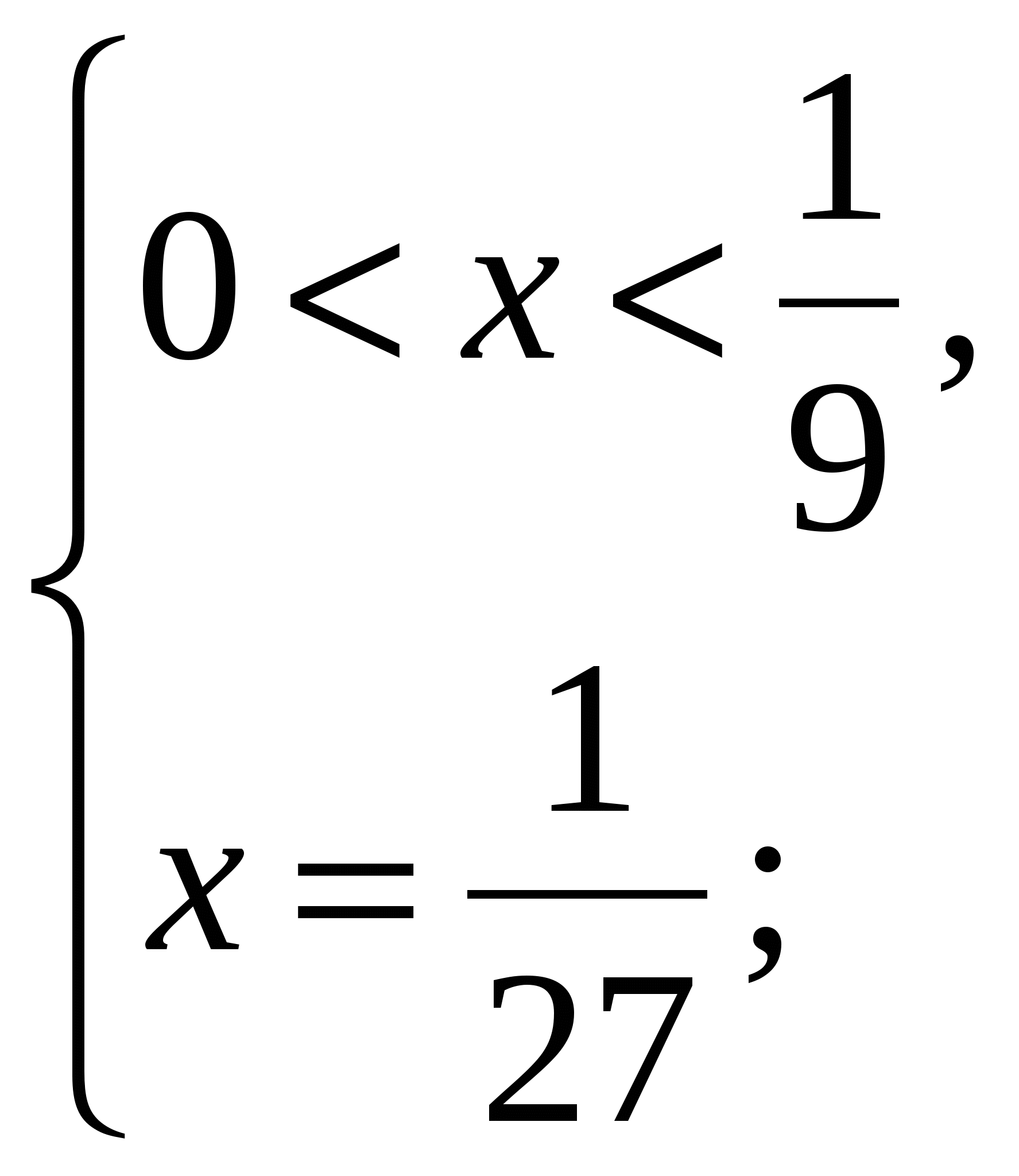
![]() ;
;
2) 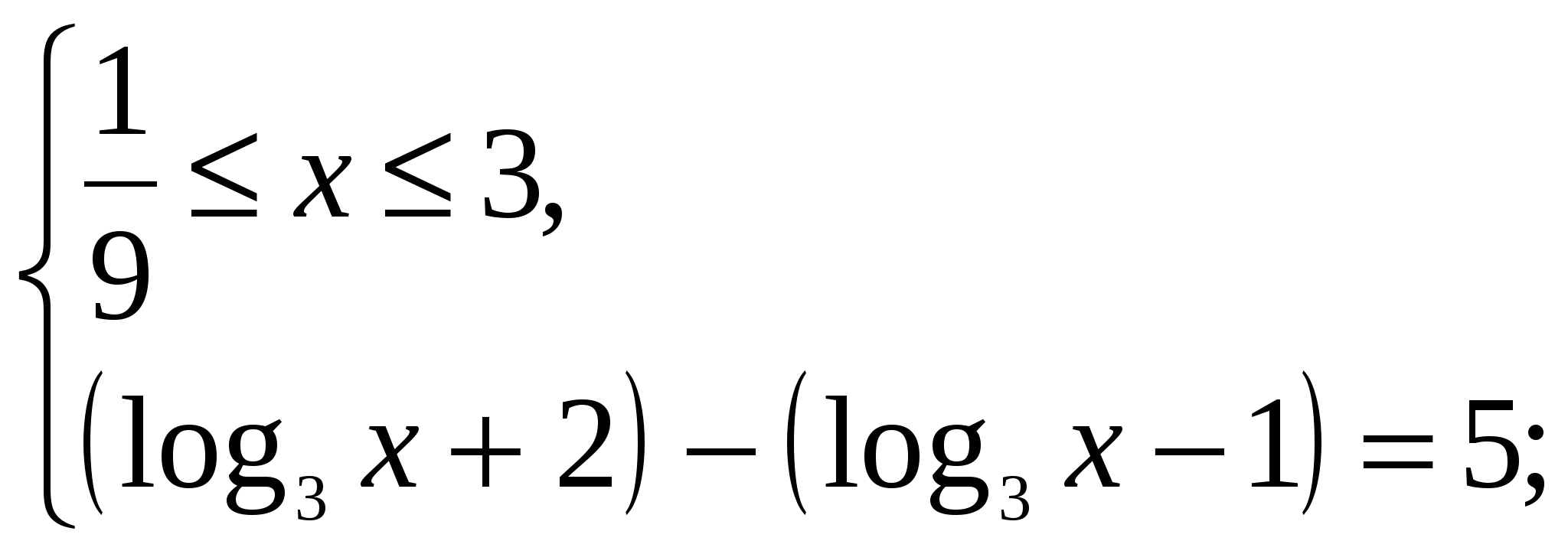
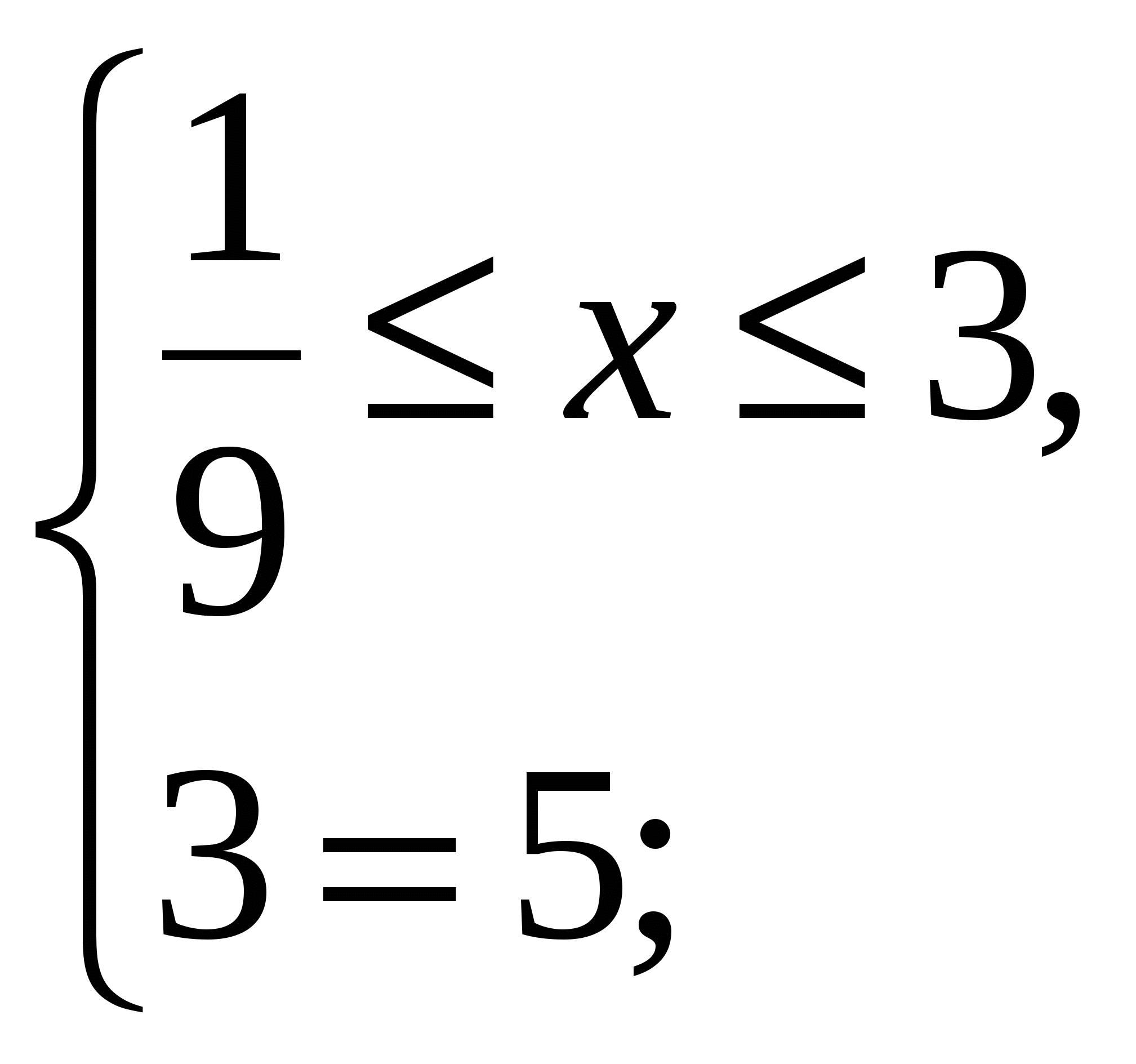 решений нет;
решений нет;
3) 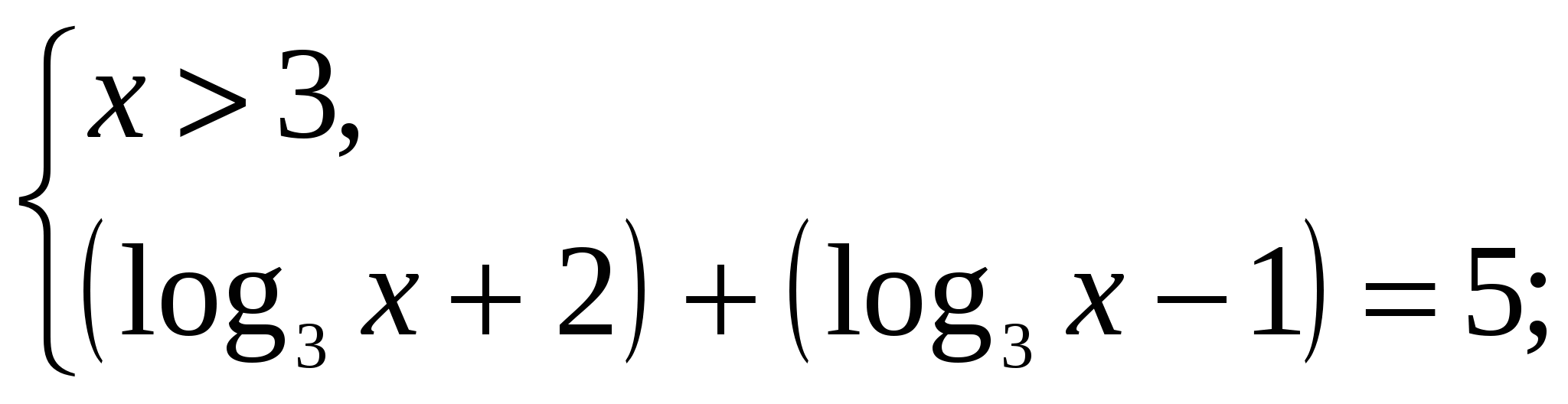

![]()
![]() .
.
Ответ находим как объединение полученных значений ![]() и
и ![]() .
.
Ответ. ![]() ,
, ![]() .
.
7) Решите уравнение ![]() .
.
Решение.
Область определения определяется условием ![]() ,
, ![]() при
при ![]() .
.
Запишем уравнение с учетом формулы сокращенного умножения в виде:
![]() ,
, ![]() .
.
Нули выражений, стоящих под знаками модулей:
![]() ,
, ![]() ,
,
![]() ;
; ![]() .
.
Числовая ось разбивается полученными значениями на три числовых промежутка, на которых подмодульные выражения сохраняют знак.
|
|
|
| |
|
| — | + | + |
|
| — | — | + |
Раскроем в уравнении знаки модулей на полученных промежутках по определению:
1) 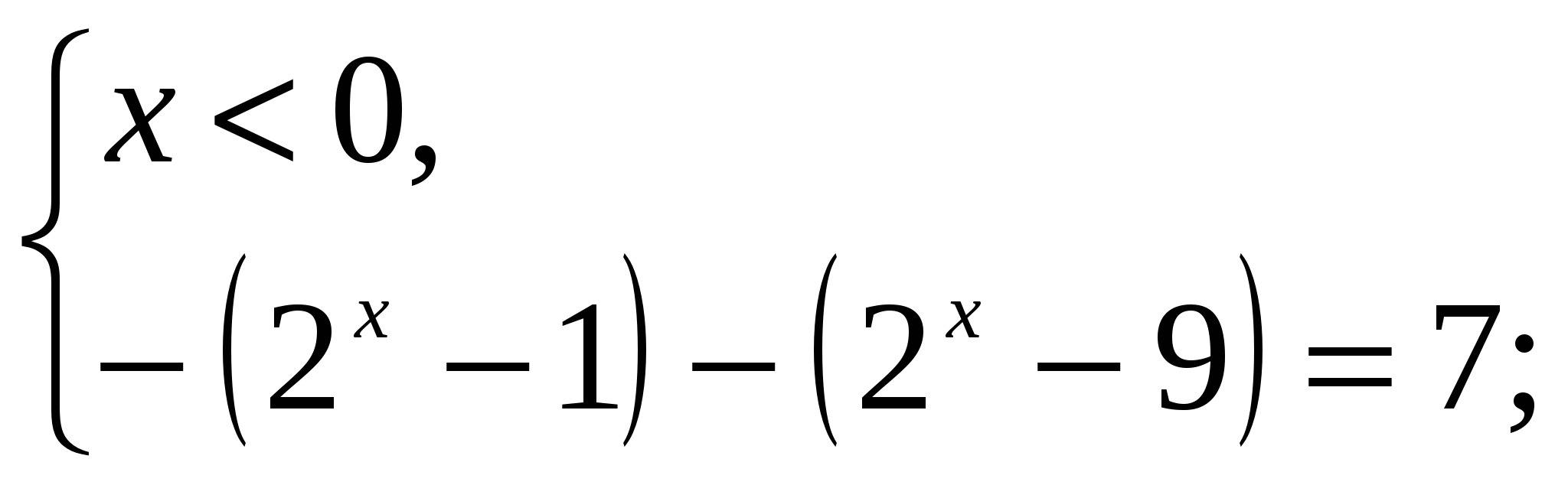

 решений нет;
решений нет;
2) 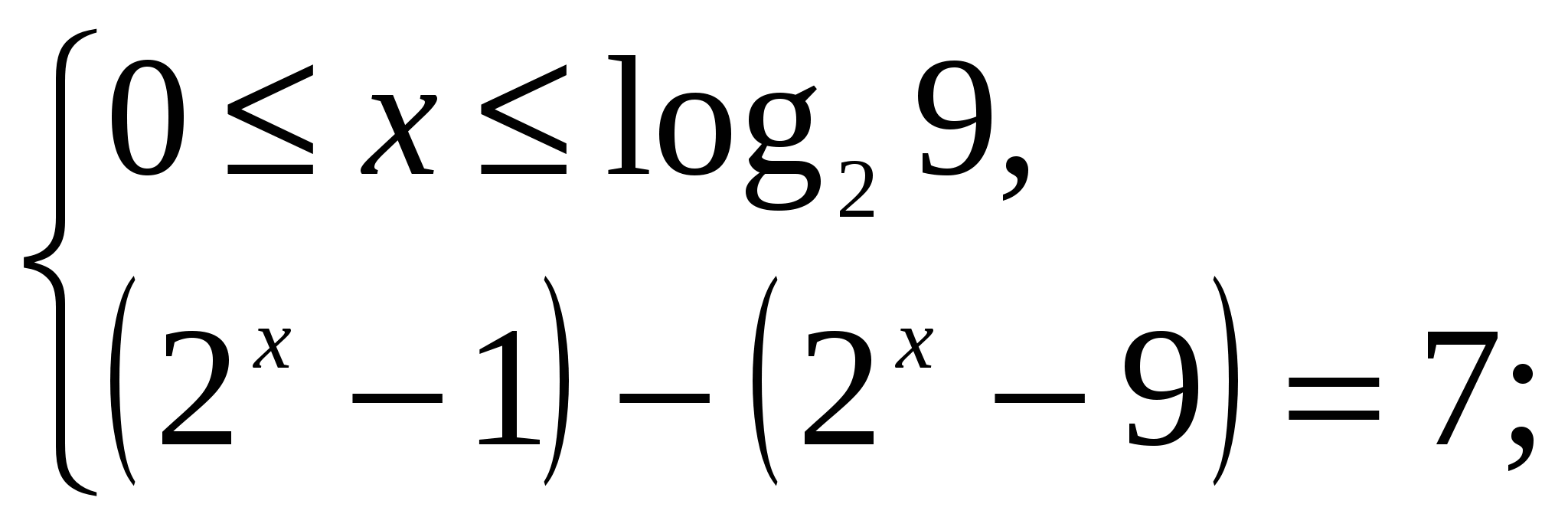
 решений нет;
решений нет;
3) 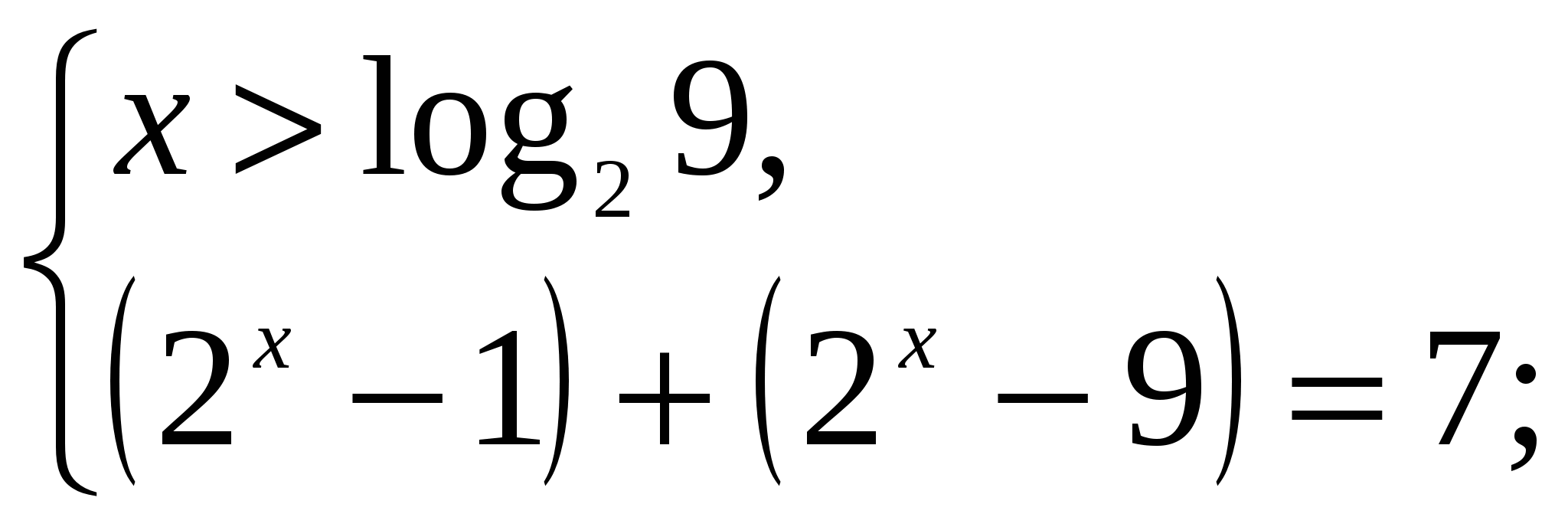
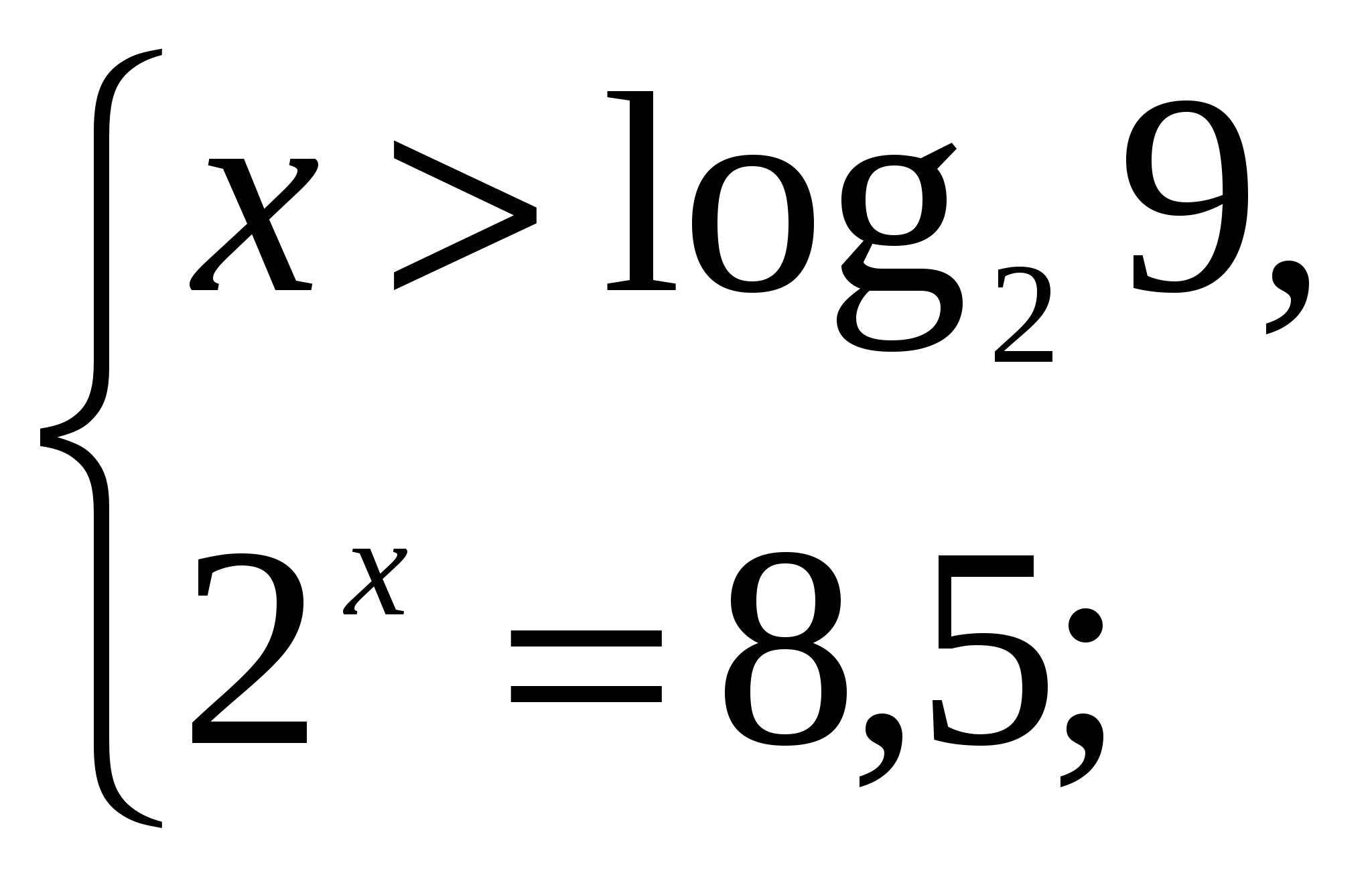
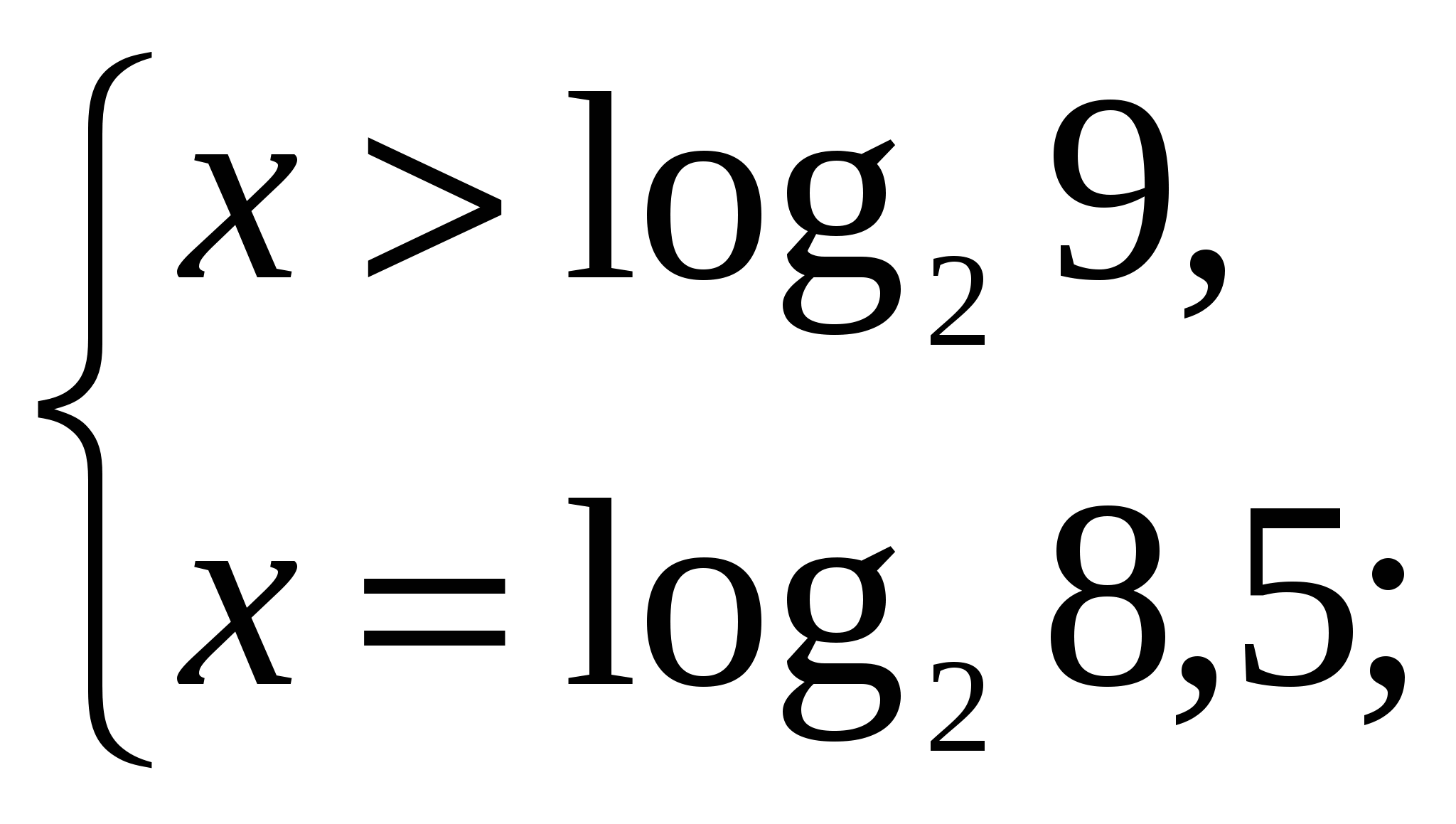 решений нет.
решений нет.
Ответ. Корней нет.
8) Решите уравнение ![]() .
.
Решение.
Это задание относится к типу «модуль под модулем», или уравнение с «вложенными модулями», которые нужно последовательно раскрыть.
В данной задаче посмотрим способ раскрытия внешнего модуля.
Уравнение равносильно совокупности двух уравнений:
а) ![]() , б)
, б) ![]() ,
,
![]() ,
, ![]() ,
,
корней нет, т. к. ![]() при
при ![]() ;
; ![]() ,
,
![]() ,
, ![]() .
.
Ответ. ![]() ,
, ![]() .
.
9) Решите уравнение ![]()
Решение.
Область определения уравнения находится из условия ![]() ,
, ![]() ,
,
получаем ![]() и
и ![]() .
.
По свойству модулей ![]()
![]()
![]()
Данное уравнение равносильно системе: 
![]() ,
,
![]() , с учетом возрастания логарифмической функции с основанием 3 на всей области определения, получаем
, с учетом возрастания логарифмической функции с основанием 3 на всей области определения, получаем ![]() ,
, ![]() , т. е.
, т. е.
![]() и
и ![]() .
.

![]() .
.
Ответ. ![]() .
.
Неравенства с модулями.
1) Решите неравенство ![]() .
.
Решение.
С учетом формулы квадрата суммы, получаем равносильное неравенство
![]() или
или ![]() .
.
Решим полученное неравенство с модулями методом интервалов:
![]() ,
, ![]() ,
, ![]() ,
,
![]() ;
; ![]() ;
; ![]() .
.
Полученные значения разбивают числовую ось на четыре числовых промежутка. Определим знаки подмодульных выражений на этих промежутках знакопостоянства:
|
|
|
|
| |
|
| — | — | — | + |
|
| — | — | + | + |
|
| — | + | + | + |
Раскроем знаки модулей на полученных числовых промежутках по определению модуля:
1) 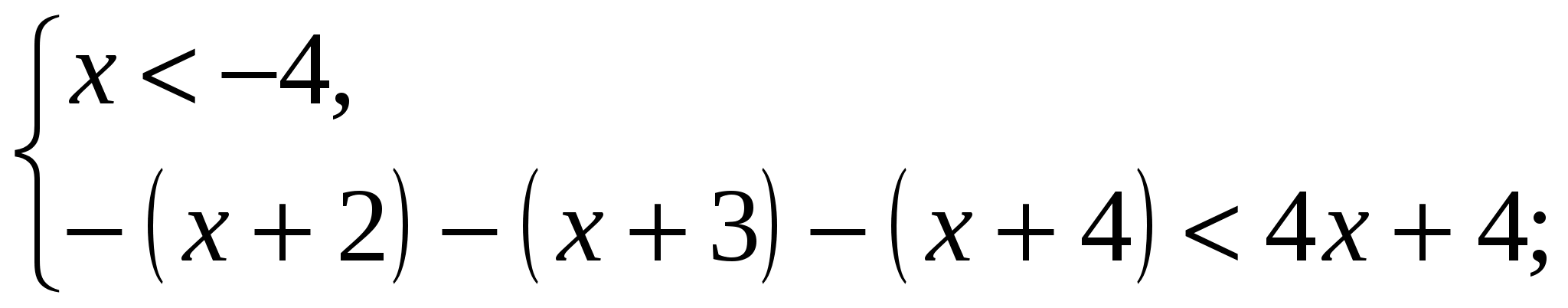
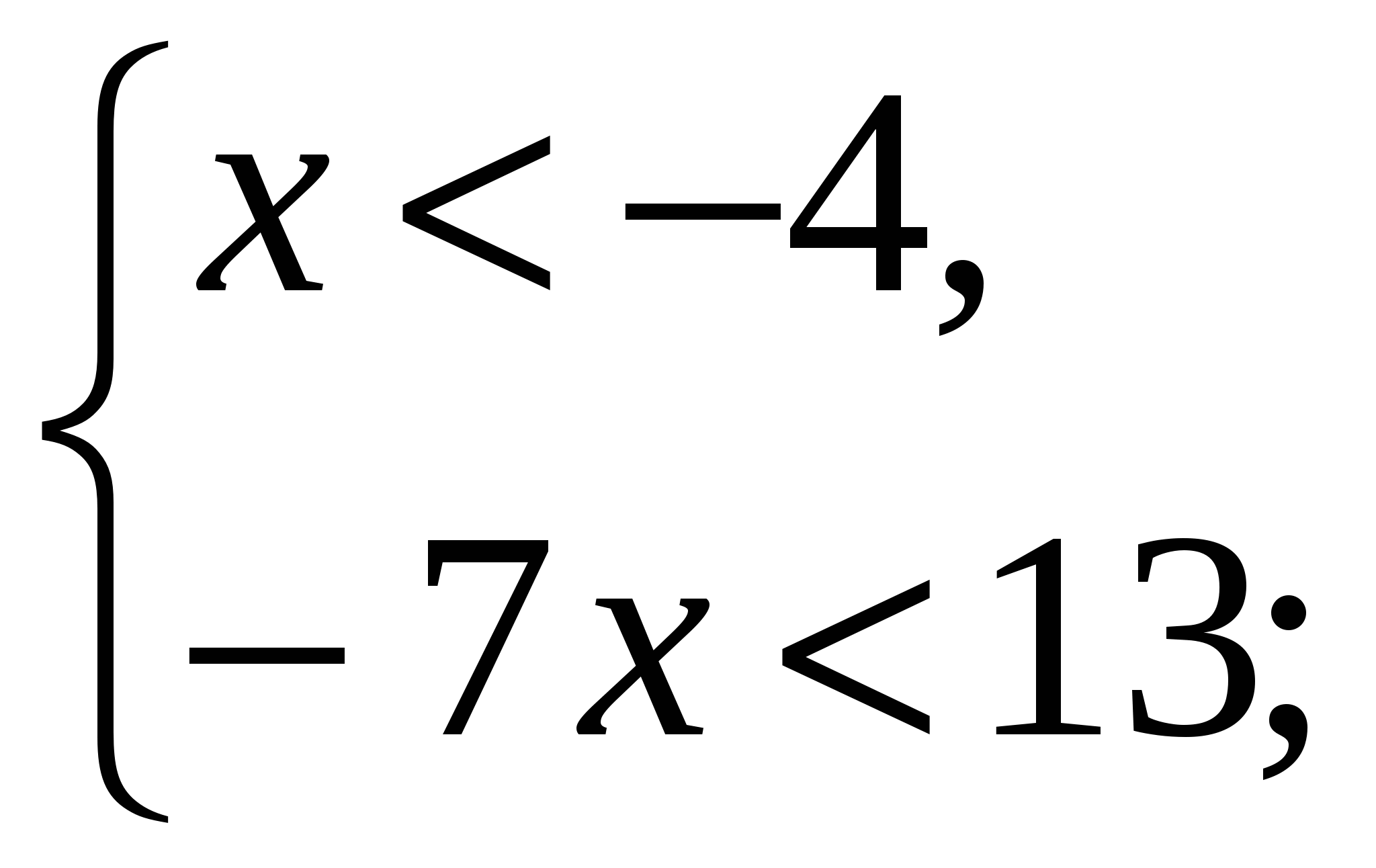
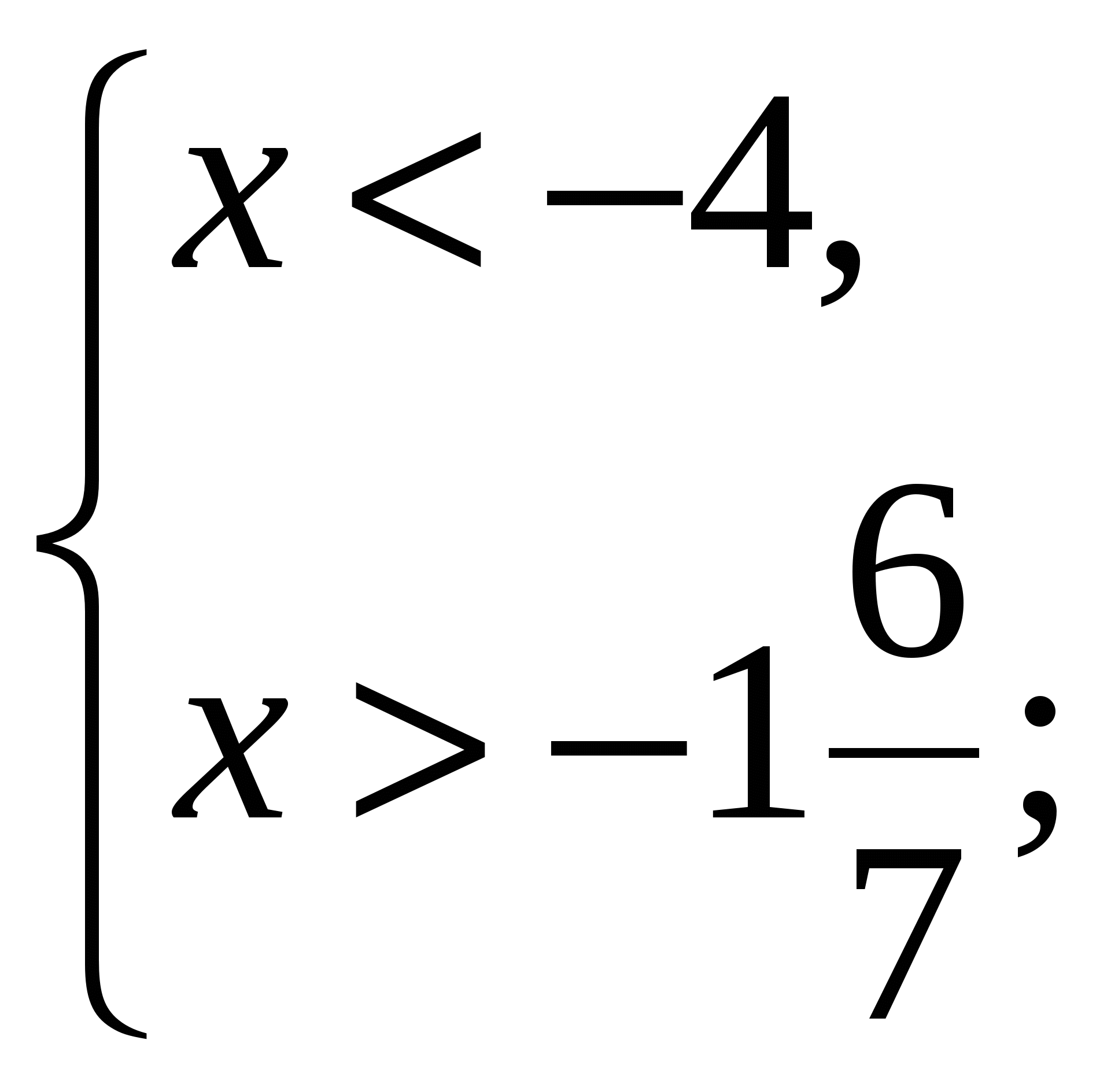 решений нет;
решений нет;
2) 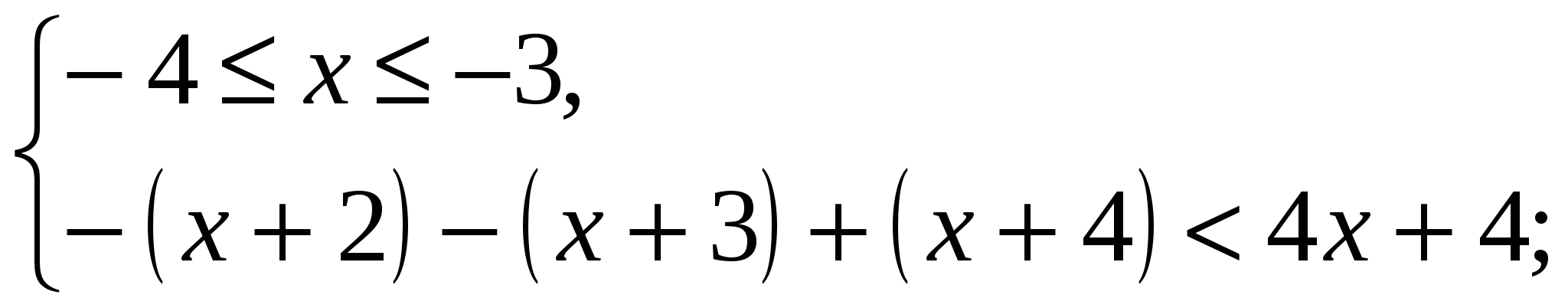
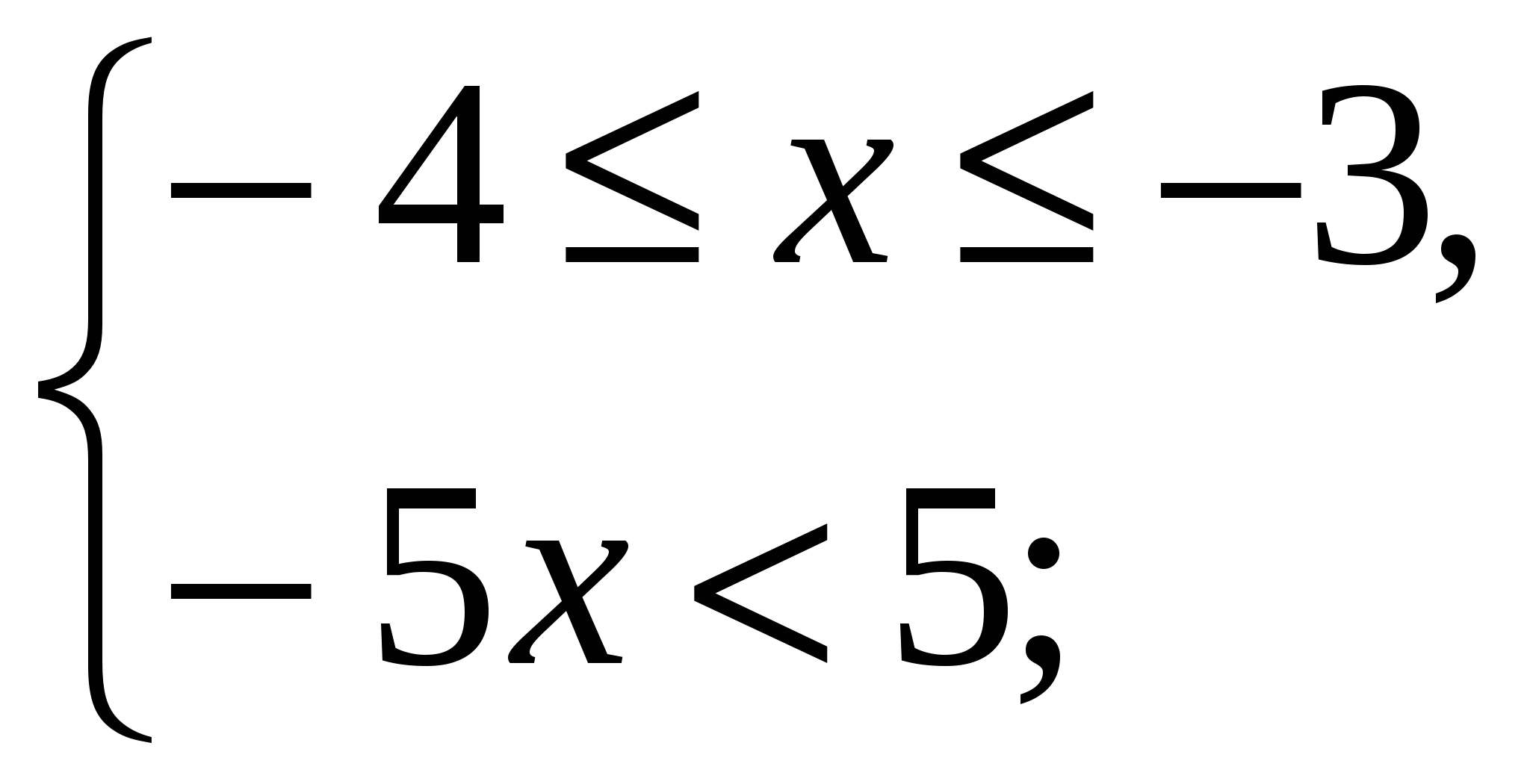
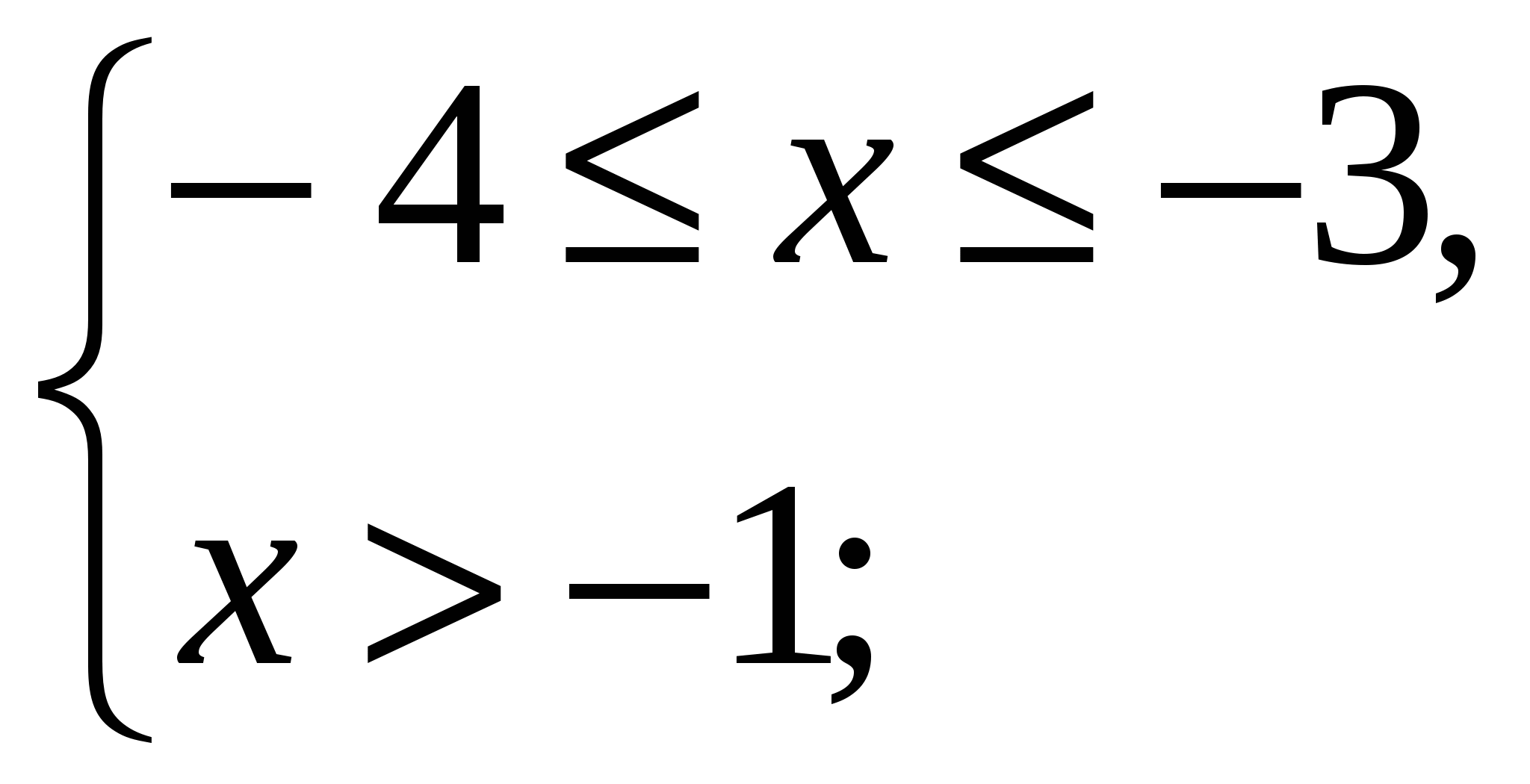 решений нет;
решений нет;
3) 
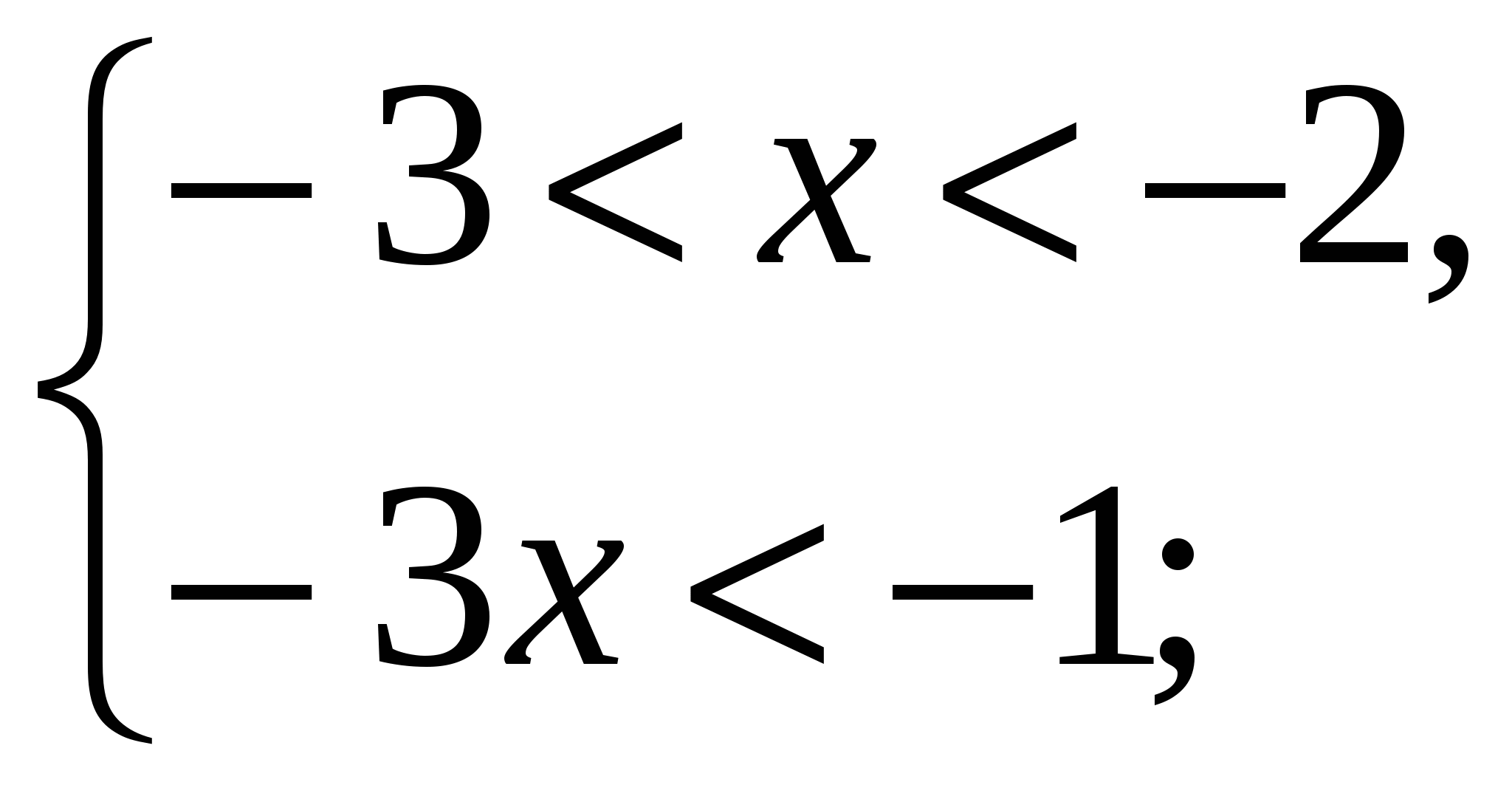
 решений нет;
решений нет;
4) 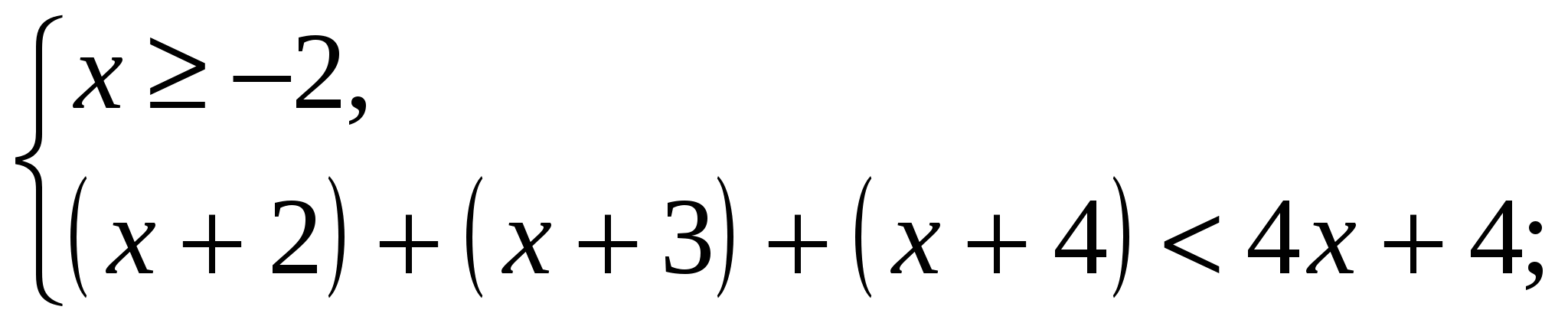

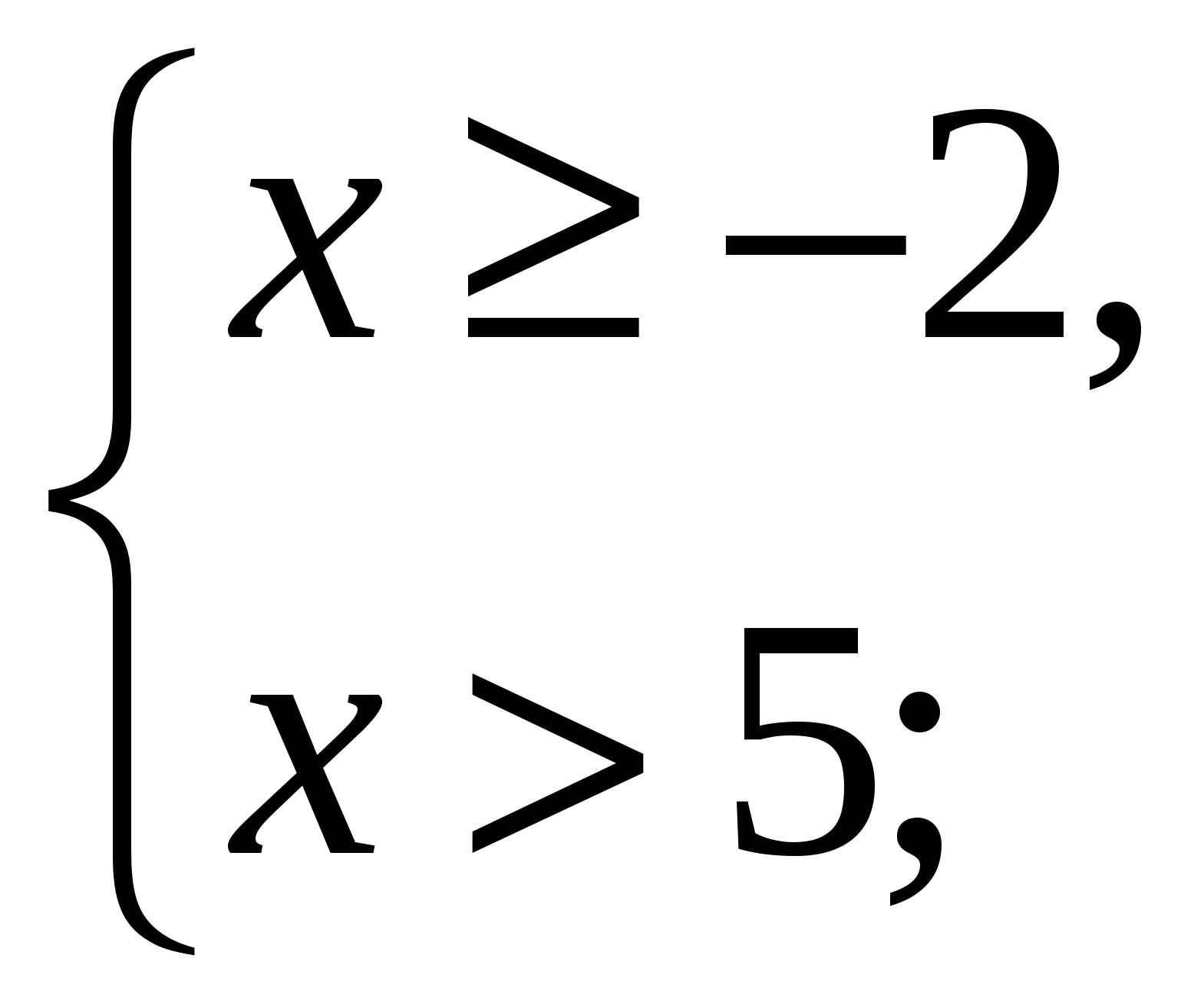
![]() .
.
Ответ. ![]() .
.
2) Укажите наибольшее целое число, которое не входит в область определения функции ![]() .
.
Решение.
В область определения данной функции входит множество положительных чисел, следовательно, любое отрицательное число и ноль не входят в область определения этой функции. Составим неравенство ![]() или
или ![]() . Полученное неравенство равносильно двойному неравенству
. Полученное неравенство равносильно двойному неравенству ![]() ,
,
![]() ,
, ![]() . Наибольшее целое решение неравенства – число 13.
. Наибольшее целое решение неравенства – число 13.
Ответ. 13
3) Найти наименьшее и наибольшее целые числа, являющиеся решениями неравенства ![]() .
.
Решение.
Раскроем внешний модуль. Данное неравенство равносильно двойному неравенству ![]() или системе неравенств:
или системе неравенств:
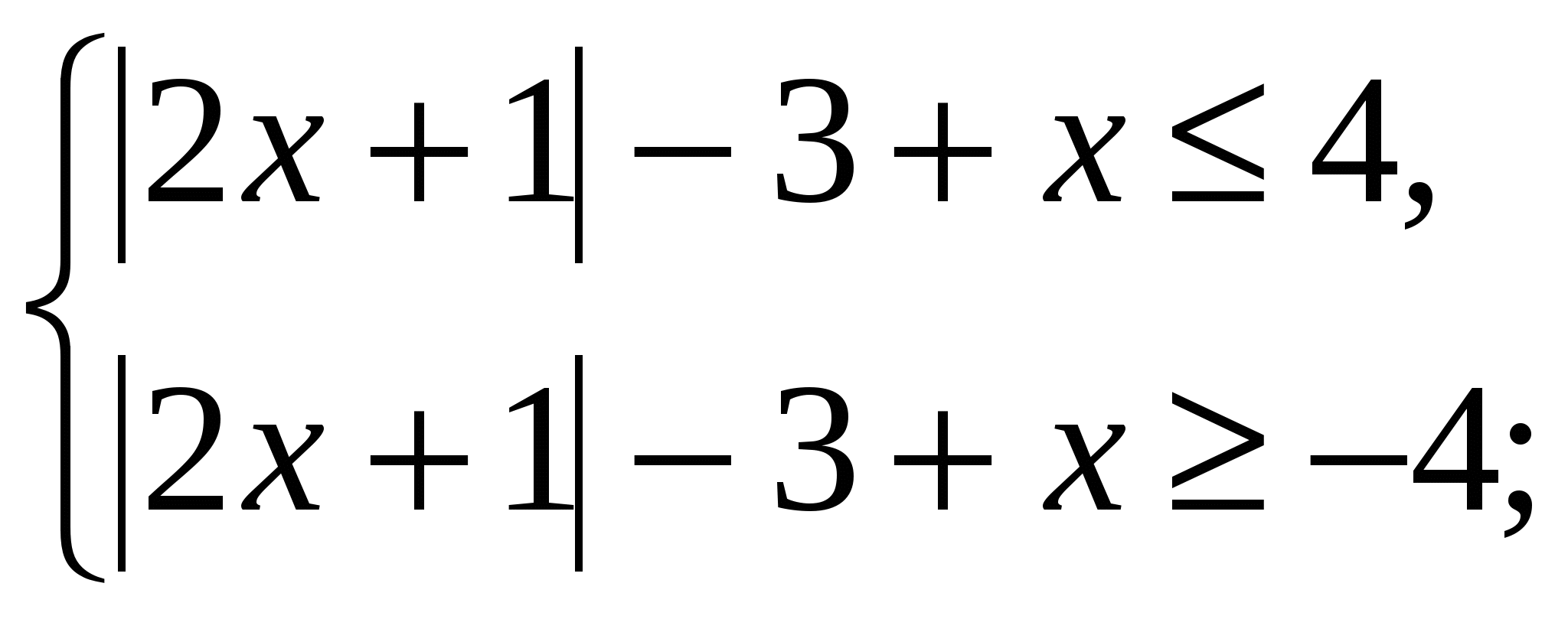
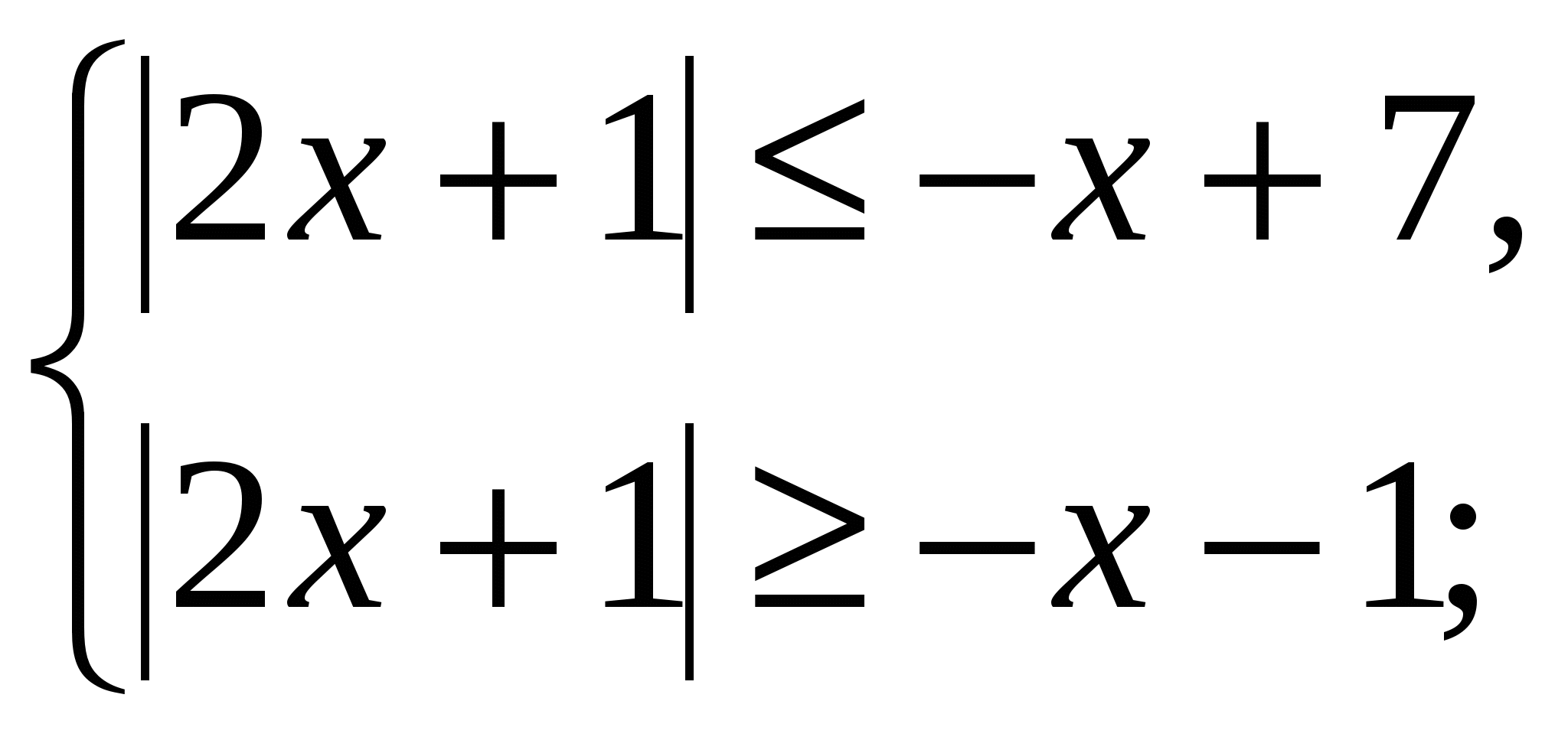
решим отдельно каждое неравенство системы:
а) ![]() , используем правило «раскрытия модуля снаружи», получаем равносильное неравенство
, используем правило «раскрытия модуля снаружи», получаем равносильное неравенство ![]() или
или
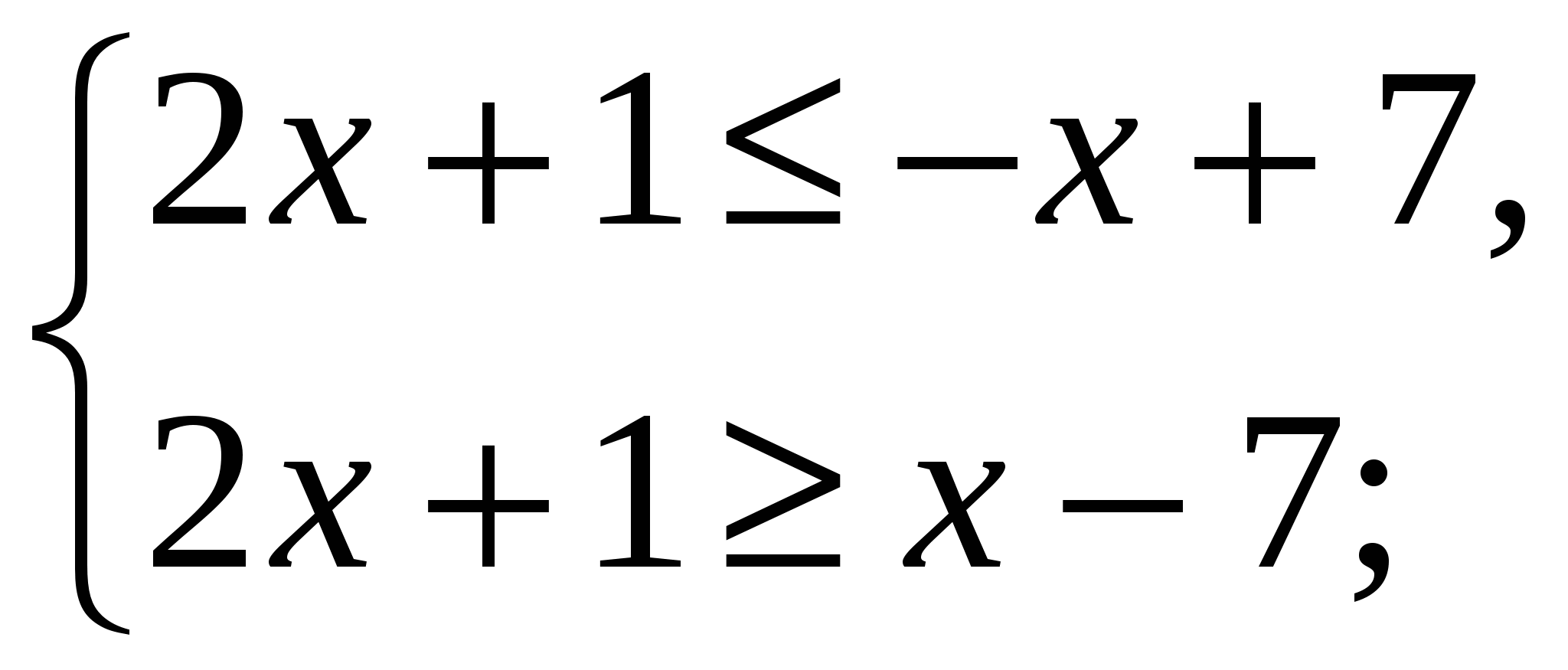

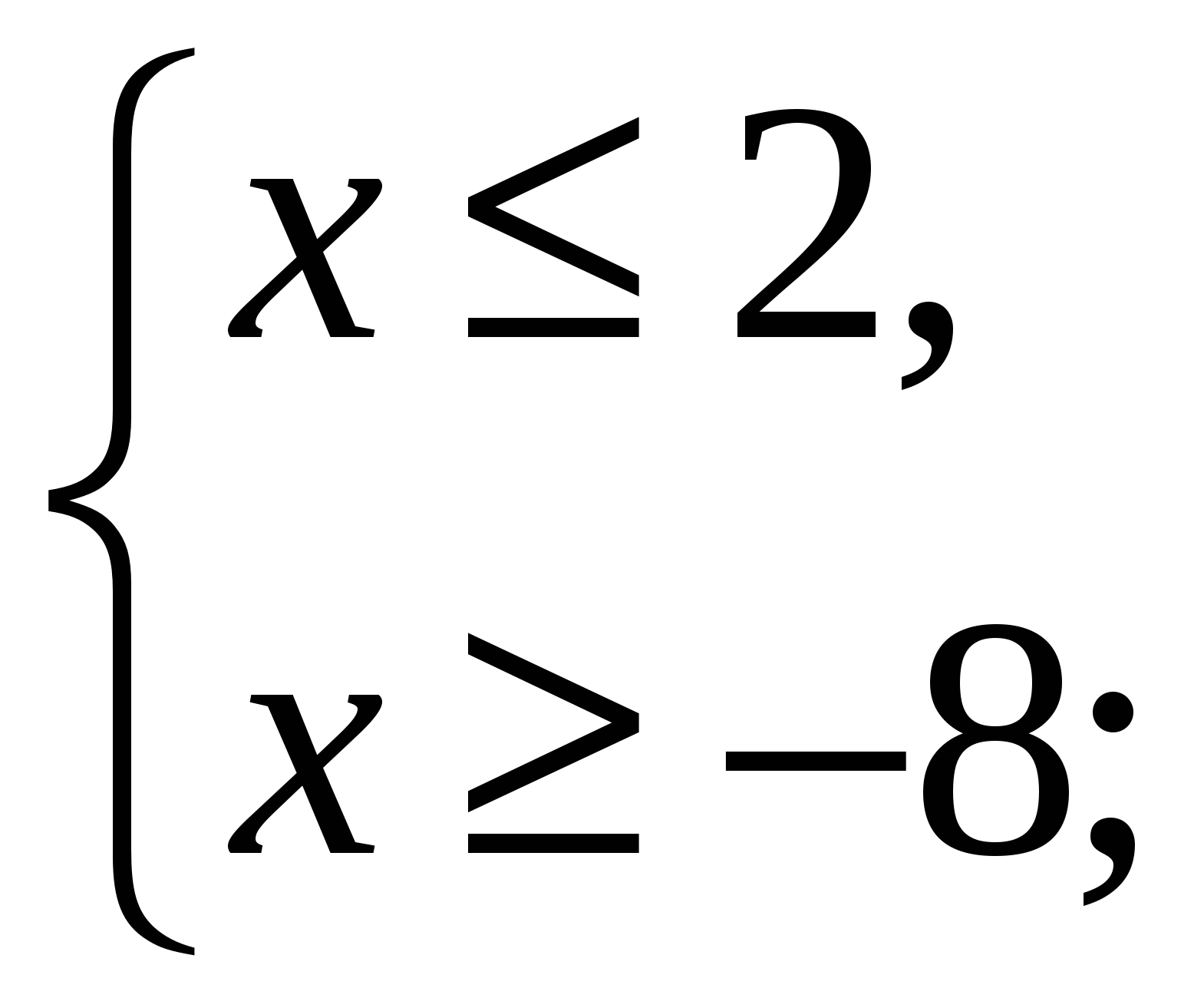
![]() ;
;
б) ![]() , используем правило «раскрытия модуля снаружи», получаем равносильную совокупность неравенств:
, используем правило «раскрытия модуля снаружи», получаем равносильную совокупность неравенств:
![]()
![]()
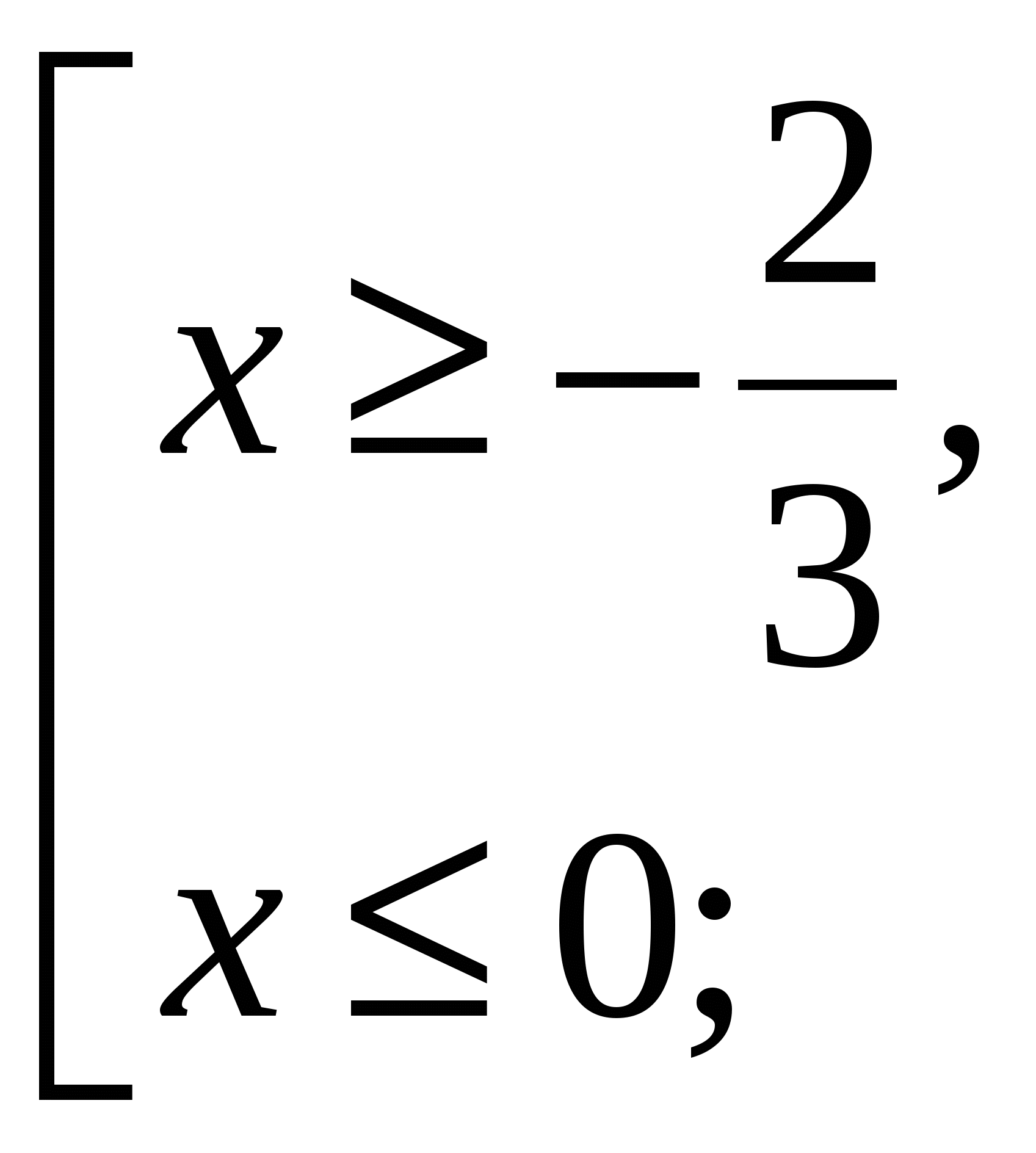
![]() ;
;
найдем решения полученной системы: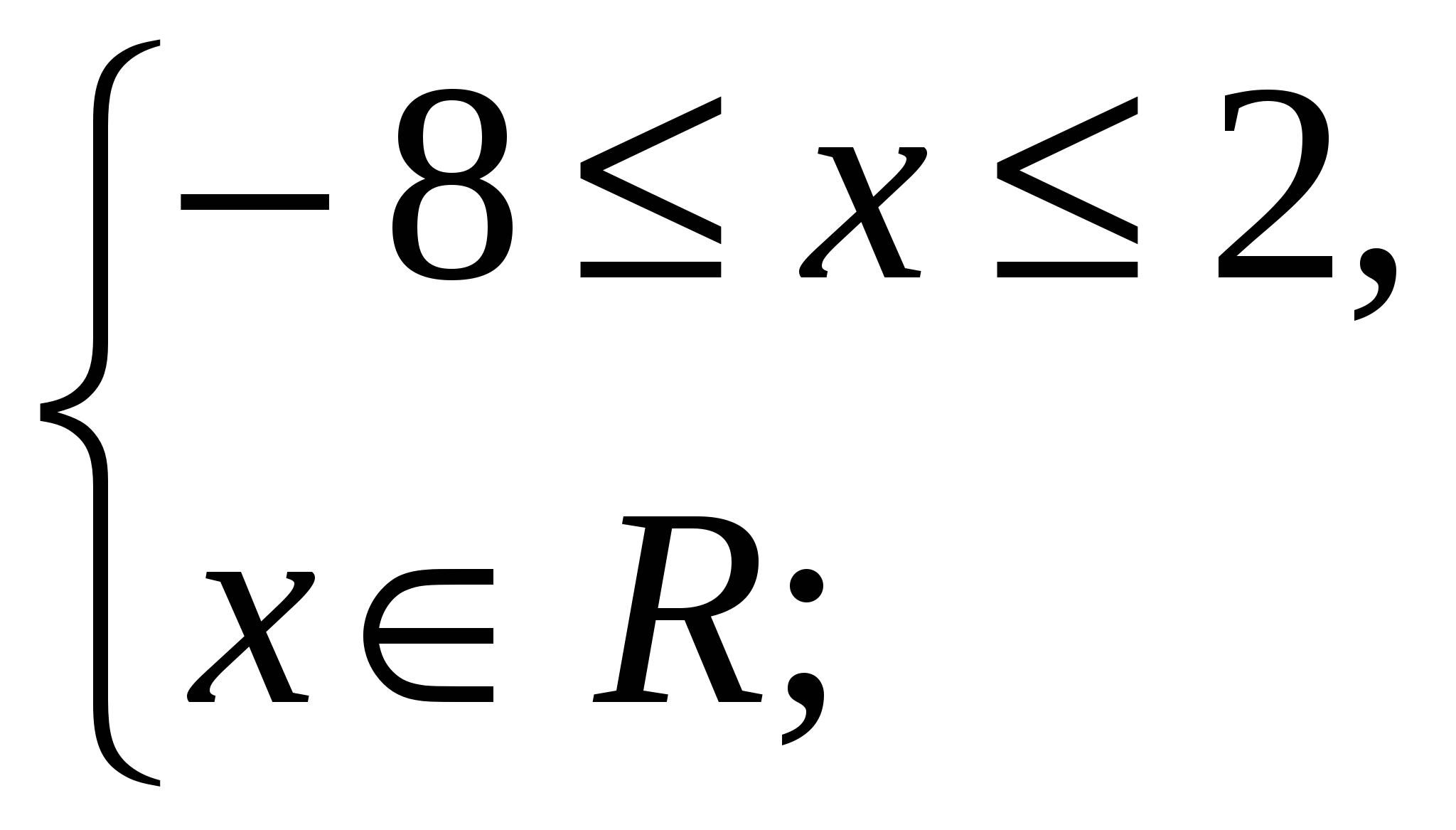
![]() .
.
Наименьшее и наибольшее целые числа, являющиеся решениями неравенства: ![]() и
и ![]() .
.
Ответ.![]() ;
; ![]() .
.
4) Решить неравенство ![]() .
.
Решение.
Область определения неравенства: ![]() .
.
Данное неравенство равносильно неравенству ![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
1)![]() не является решением неравенства;
не является решением неравенства;
2) при ![]() : а)
: а) ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , тогда
, тогда
![]() при
при ![]() и, следовательно,
и, следовательно,
![]() — решения неравенства;
— решения неравенства;
б) ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() , тогда
, тогда ![]() ,
,
![]() при
при ![]() и, следовательно,
и, следовательно,
![]() — решения неравенства;
— решения неравенства;
получаем, что ![]() — решения неравенства;
— решения неравенства;
3) функция ![]() является четной, т. к.
является четной, т. к. ![]() , тогда
, тогда
![]() являются решениями неравенства.
являются решениями неравенства.
Ответ. ![]() ,
, ![]() .
.
5) Решить неравенство ![]() .
.
Решение.
Неравенство вида ![]() можно решить по алгоритму:
можно решить по алгоритму:
если ![]() то все
то все ![]() из области определения системы – решения неравенства;
из области определения системы – решения неравенства;
если ![]() то
то ![]() .
.
Область определения неравенства определяется условием ![]() , т. е.
, т. е. ![]() .
.
1) если ![]() ,
,
![]() ,
,
если ![]() , то нет решений полученного неравенства,
, то нет решений полученного неравенства,
если ![]() , то обе части неравенства положительные и можно возвести в квадрат, получаем
, то обе части неравенства положительные и можно возвести в квадрат, получаем ![]() ,
, ![]() ,
,
![]() и
и ![]() , т. к.
, т. к. ![]() , то
, то
![]() — решения неравенства;
— решения неравенства;
2) если ![]() , т. е.
, т. е. ![]() , то обе части исходного неравенства можно возвести в квадрат, получаем:
, то обе части исходного неравенства можно возвести в квадрат, получаем:
![]() ,
,
![]() ,
,
![]() , тогда
, тогда ![]() ,
, ![]() ;
;
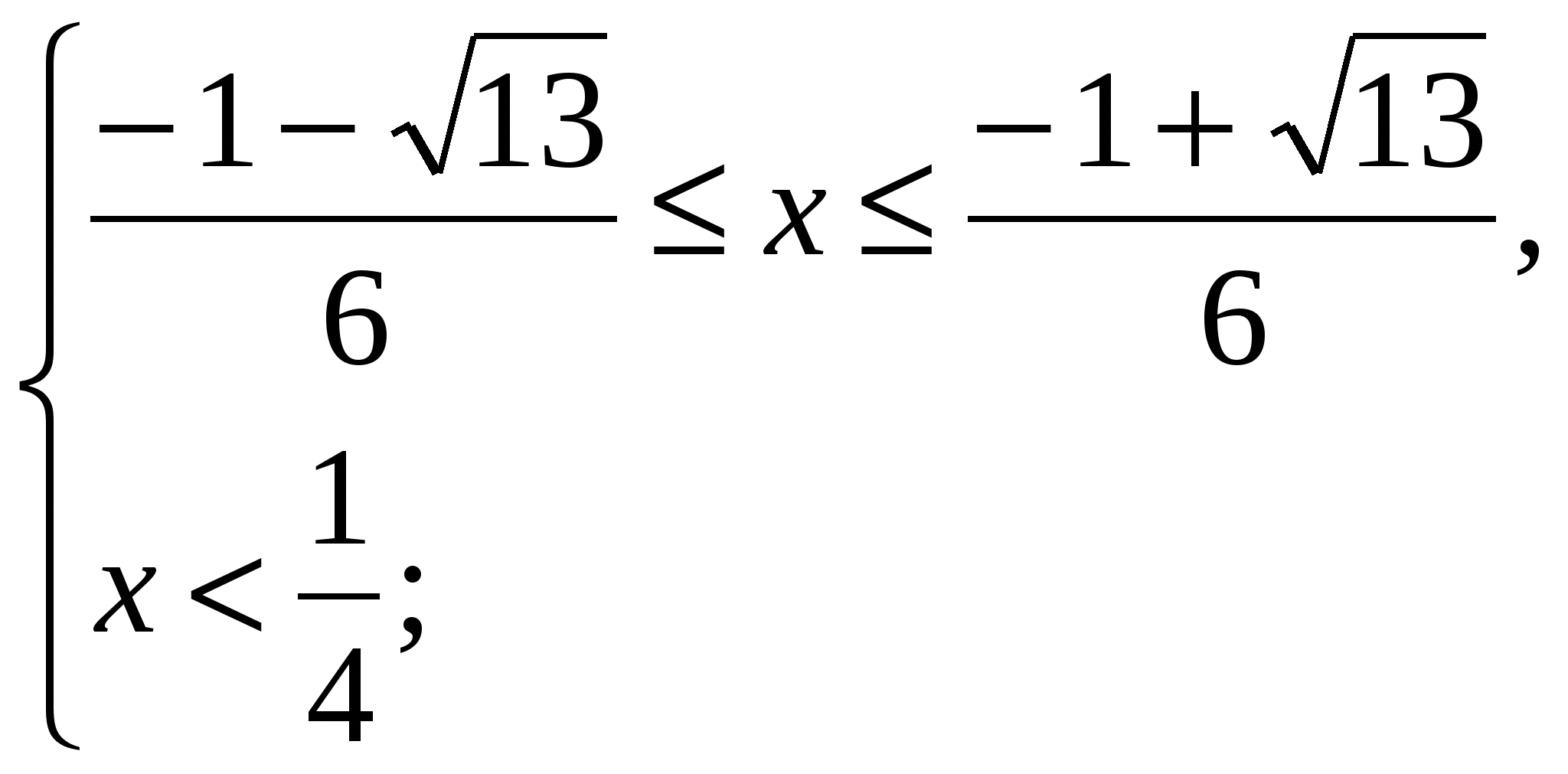
![]() .
.
Объединяя условия ![]() и
и ![]() получаем решения исх. нерав.
получаем решения исх. нерав. ![]() .
.
Ответ. ![]() .
.
Задания с параметрами.
1) При каких значениях ![]() уравнение
уравнение ![]() а) не имеет корней;
а) не имеет корней;
б) корни принадлежат отрезку ![]() .
.
Решение.
Пусть ![]() . Найдем нуль подмодульного выражения
. Найдем нуль подмодульного выражения
![]() ,
, ![]() .
.
если ![]() , то
, то ![]() ,
, ![]() , угловой коэффициент полученной прямой отрицательный, тогда функция убывает до
, угловой коэффициент полученной прямой отрицательный, тогда функция убывает до ![]() ;
;
если ![]() , то
, то![]() ,
,![]() , угловой коэффициент полученной прямой положительный, тогда функция возрастает от
, угловой коэффициент полученной прямой положительный, тогда функция возрастает от ![]() .
.
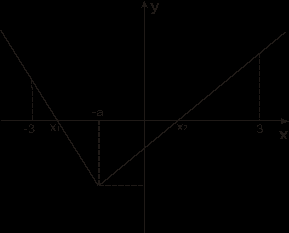
а) чтобы данное уравнение не имело корней, необходимо и достаточно, чтобы наименьшее значение функции было положительным, т. е. ![]() .
.
![]() , это условие выполняется при
, это условие выполняется при ![]() и
и ![]() .
.
б) чтобы существовали корни, достаточно требовать ![]() ,
, ![]() и
и![]() .
.

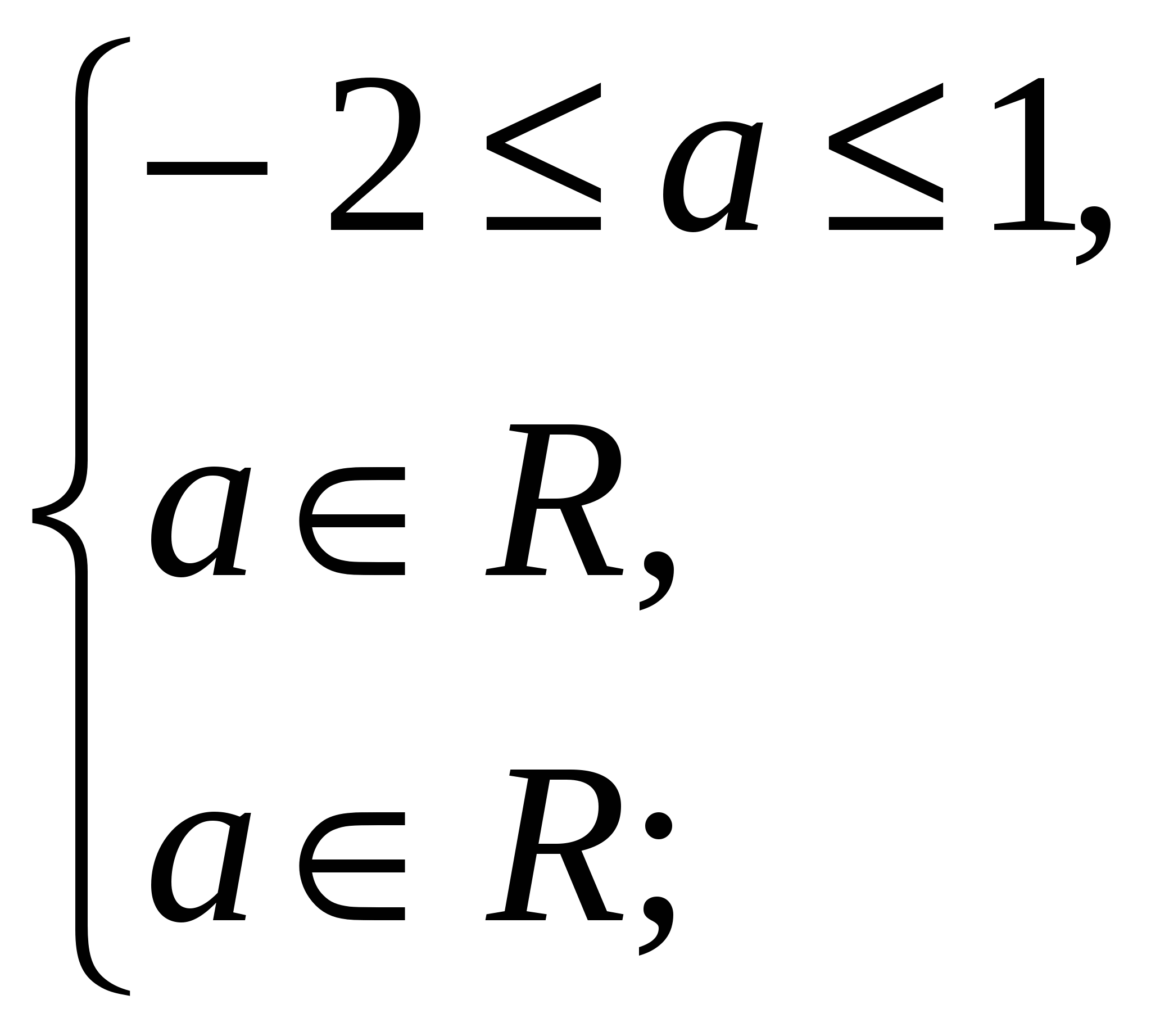
![]() .
.
Ответ. а) ![]() ,
, ![]() ; б)
; б) ![]() .
.
2) Найти все значения ![]() , при каждом из которых неравенство
, при каждом из которых неравенство ![]() выполняется для любого
выполняется для любого ![]() .
.
Решение.
Рассмотрим функцию ![]() , нужно найти все значения
, нужно найти все значения ![]() , при которых
, при которых ![]() .
.
Найдем нули подмодуульных выражений:


1) Если ![]() и
и ![]() , то функция
, то функция ![]() ,
,
![]() убывает и принимает наименьшее значение при
убывает и принимает наименьшее значение при ![]() или
или ![]() ;
;
2) если ![]() находится на отрезке с концами
находится на отрезке с концами ![]() и
и ![]() , то функция монотонно возрастает;
, то функция монотонно возрастает;
3) если ![]() и
и ![]() , то функция
, то функция ![]() ,
, ![]() возрастает и принимает наименьшее значение при
возрастает и принимает наименьшее значение при ![]() или
или ![]() .
.
Тогда функция ![]() принимает наименьшее значение при
принимает наименьшее значение при ![]() или
или ![]() .
.
Чтобы выполнялось при всех ![]() условие
условие ![]() , нужно, чтобы наименьшее значение этой функции было положительным, т. е.
, нужно, чтобы наименьшее значение этой функции было положительным, т. е. 
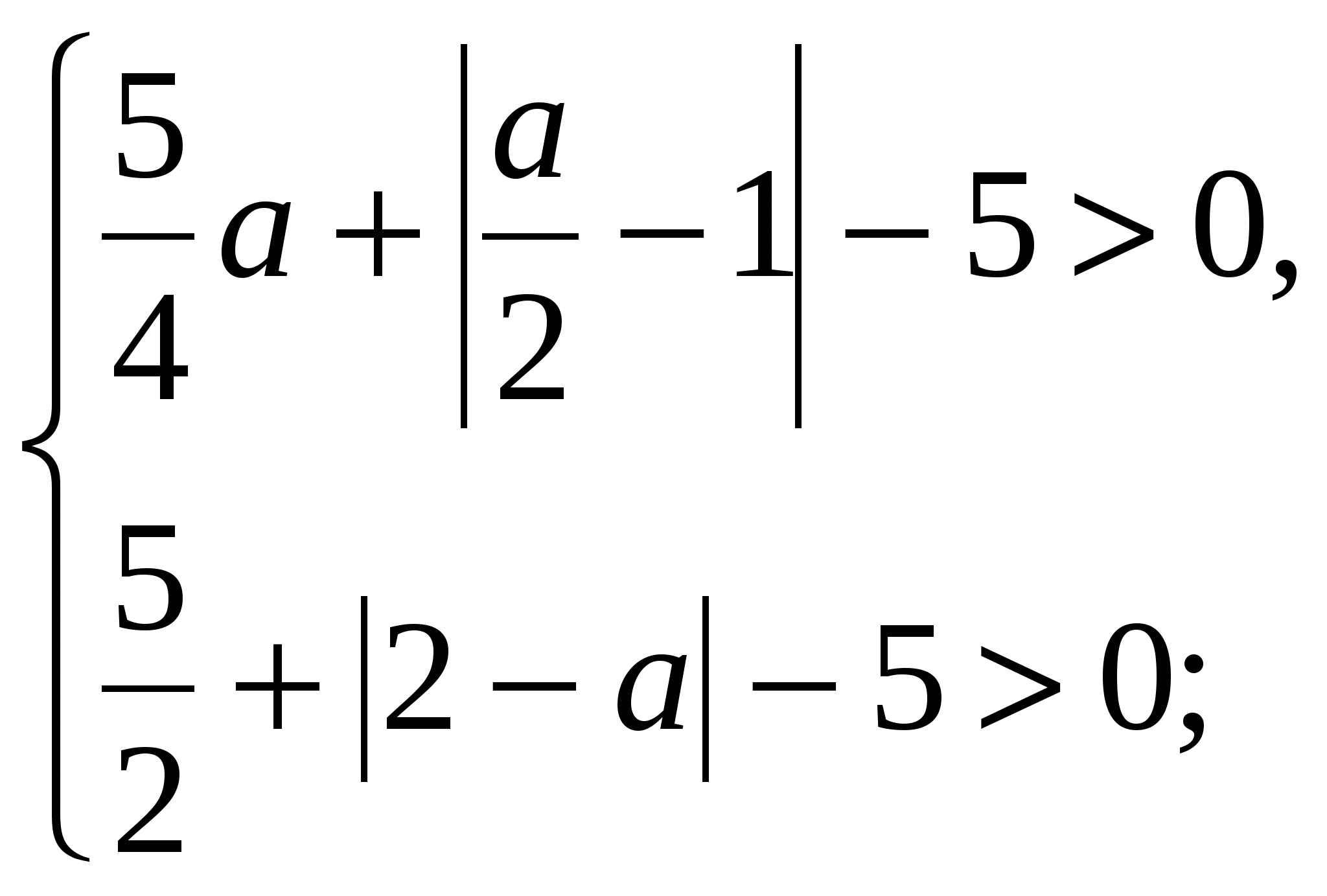

![]() .
.
Ответ. ![]() 3) Найти все значения
3) Найти все значения ![]() , при каждом из которых функция
, при каждом из которых функция ![]() имеет ровно три нуля функции.
имеет ровно три нуля функции.
Решение.
Составим уравнение ![]() , запишем его в виде
, запишем его в виде ![]() и решим графическим способом.
и решим графическим способом.
Пусть ![]() и
и ![]() . Необходимо найти условие пересечения графиков в трех точках. Тогда у уравнения
. Необходимо найти условие пересечения графиков в трех точках. Тогда у уравнения ![]() будет три корня и у функции
будет три корня и у функции ![]() ровно три нуля.
ровно три нуля.
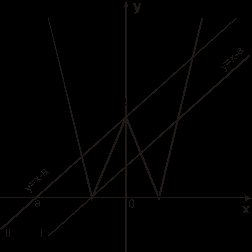
При ![]() уравнение имеет единственный корень.
уравнение имеет единственный корень.
Из семейства параллельных прямых ![]() нас интересуют только те, которые пересекают построенный график в трех точках. Очевидно, что таких прямых только две. Они и построены на рисунке.
нас интересуют только те, которые пересекают построенный график в трех точках. Очевидно, что таких прямых только две. Они и построены на рисунке.
Для прямой I имеем ![]() , тогда
, тогда ![]() .
.
Для прямой II имеем ![]() , тогда
, тогда ![]()
Ответ. ![]() ,
, ![]() .
.
Литература.
Виленкин Н. Я. Алгебра и математический анализ. 10 класс. Учебник для углубленного изучения математики в общеобр. учрежд. – М.: Мнемозина, 2005 – 335 с.
Глазков Ю. А. Математика. ЕГЭ: сборник заданий и методических рекомендаций.- М.: Экзамен, 2010.-333 с.
Горнштейн П.И. и др. Задачи с параметрами. М.: Илекса, 1999.- 336 с.
Григорьева Т. П. и др. Пособие по элементарной математике: методы решения задач. Часть 2. – Н. Новгород: НГПУ, 2001.- 101 с.
Жафяров А. Ж. Математика. ЕГЭ. Решение задач уровня С1. Учебное пособие.- Новосибирск: Сиб. унив. изд-во, 2009.-181 с.
Жафяров А.Ж. Математика. ЕГЭ 2010. Экспресс-консультация.-Новосибирск: Сиб. унив. изд-во, 2010.-218 с.
Кочагин В. В. ЕГЭ 2010. Математика: Сборник заданий. – М.: Эксмо, 2009. – 208 с.
Макарычев Ю. Н. и др. Алгебра. 9 кл.: Учебник для школ и классов с углубленным изучением математики.- М.: Мнемозина, 2004. – 439 с.
Макарычев Ю. Н. и др. Алгебра: Дополнительные главы к школьному учебнику 9 кл. – М.: Просвещение, 2000. – 224 с.
Математика. 8-9 классы: сборник элективных курсов. Вып.1/ авт.-сост.В. Н. Студенецкая, Л. С. Сагателова.- Волгоград: Учитель, 2007.-205 с.
Мерзляк А. Г. и др. Алгебраический тренажер: Пособие для школьников и абитуриентов. М.: Илекса, 2005. – 320 с.
Олехник С. Н. и др. Уравнения и неравенства. Нестандартные методы решения. 10-11 классы: Учебно-метод пособие.- М.: Дрофа, 2001. – 192 с.
Олехник С. Н. и др. Уравнения и неравенства. Нестандартные методы решения. 10-11 классы: Учебно- метод. пособие. М.: Дрофа, 2001.- 192 с.
Садовничий Ю. В. Алгебра. Конкурсные задачи с решениями: учебное пособие. – М.: Экзамен, 2007. – 445 с.
Черкасов О. Ю., Якушев А. Г. Математика: Справочник для старшеклассников и поступающих в вузы. М.: АСТ-ПРЕСС ШКОЛА, 2004.- 640с.
11
