МЕТОДЫ РЕШЕНИЯ ЛОГИЧЕСКИХ ЗАДАЧ.
Подготавливая учащихся к ГИА и ЕГЭ по математике, я столкнулась с проблемой неумения учащимися решать логические задачи. В современных учебниках, начиная с 5 класса, на их решение отводится очень мало времени, и ученики не отрабатывают должным образом навыки решения логических задач. А ведь логические задачи составляют неотъемлемую часть математического образования любого школьника. Они заостряют интеллект и развивают логическое мышление, что очень важно при их подготовке к будущему обучению.
Решить такие задачи в уме, наверное, кто-то и сможет, но понятно, что не каждому это под силу. Однако решение становится прозрачным и легким для всех, если освоить несколько приемов решения логических задач.
Есть несложные задачи, для решения которых достаточно хорошей смекалки, другие задачи требуют уже более серьезной подготовки: владение техникой решения подобных задач и умением организовать работу над задачей (выявить важные условия, подобрать способ решения).
Что же представляют собой логические задачи? Логические задачи или, как их еще иногда называют, нечисловые, представляют собой текстовые задачи, в которых требуется распознать объекты или расположить их в определенном порядке по имеющимся свойствам. При этом часть утверждений условия задачи может выступать с различной истинностной оценкой (быть истинной или ложной). К классу логических задач относятся также задачи на переливания и взвешивания (фальшивые монеты и т.п.). Далее речь пойдет о методах и приемах решения таких задач.
Выделим основные методы решения логических задач и рассмотрим их подробнее по отдельности:
МЕТОД РАССУЖДЕНИЙ.
Метод рассуждений является самым простым и примитивным из всех перечисленных, потому что не требует каких-то особенных знаний и навыков. Он заключается в проведении рассуждения, используя все условия задачи, в результате которого мы приходим к результату, который и будет искомым решением. Применяя этот метод, мы можем решить относительно несложные задачи.
Задача: Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский». Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?
Решение: Имеется три утверждения. Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно. Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно. Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.
В качестве результата делаем вывод: Сергей изучает китайский язык, Михаил — японский, Вадим — арабский.
МЕТОД ТАБЛИЦ.
Метод таблиц является более сложным относительно метода рассуждений, но так же не требует от нас определенных знаний: только способность логически рассуждать и правильно оценивать условия задачи. Данный метод имеют преимущество перед методом рассуждений, так как таблицы, составляемые в ходе решения задач, позволяют наглядно представить нам условие задачи. Рассмотрим решение логической задачи методом таблиц на примере.
Задача: Жили-были две девочки: Катя и Валя. На их улице было 3 дома: один дом был с окном и трубой, другой — с окном, но без трубы, а третий — с трубой, но без окна. Каждая девочка жила в своем доме. Катя и Валя жили в домах с окнами. Валя любила тепло и часто топила печку. Кто в каком доме жил?
Решение: Составим таблицу, в клетках которой будем ставить – (ложное высказывание) эти пункты противоречат условию задачи, и ставить +(истинное высказывание), если условие совпадает. В итоге получим таблицу:
дом с окном и трубой | дом с окном, но без трубы | дом с трубой, но без окна | | Катя | _ | + | _ |
| Валя | + | _ | _ |
В результате получаем ответ: Катя живет в доме с окном, но без трубы, а Валя — в доме с окном и трубой.
МЕТОД ГРАФОВ.
Метод графов уже требует определенных знаний и навыков. Прежде чем перейти к решению задачи ответим на простой вопрос: «А что такое граф?».
Графом называется способ представления, при котором объекты изображаются точками, а связи между ними линиями или стрелками. Примером графа может служить схема метро. Точки называются вершинами графа, а линии – ребрами.
Решение задач этим методом заключается в построении графа по условию задачи: дело нелегкое, но интересное.
Задача: Встретились три друга: Белов, Краснов и Чернов. Один из них был в черной рубашке, другой в красной, а третий в белой. Мальчик в красной рубашке говорит Чернову: «Нам надо поменяться рубашками, а то цвет наших рубашек не соответствует нашим фамилиям». Кто из мальчиков в какую рубашку был одет?
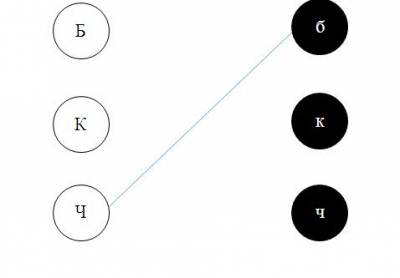
Решение: Здесь мы имеем два равночисленных множества: множество фамилий и множество цветов рубашек. Между этими множествами надо установить взаимно-однозначное соответствие. Для этого построим граф. Пусть белые кружочки Б, К и Ч изображают элементы первого множества (Белов, Краснов и Чернов), а черные кружочки б, к и ч – элементы второго множества – белая, красная и чёрная. Условимся соединять эти кружочки тонкой синей линией, если между ними нет соответствия. Если же соответствие между кружочками установлено правильно, то будем соединять их жирной черной линией.
Из первого условия получаем, что мальчик в белой рубашке может быть Черновым:
И з второго условия (цвет рубашки не соответствует фамилии) следует, что Б не соответствует б, К – к и Б – б:
з второго условия (цвет рубашки не соответствует фамилии) следует, что Б не соответствует б, К – к и Б – б:
Т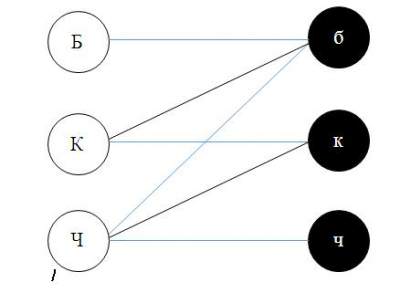 еперь из чертежа видно, что кружку Ч может соответствовать лишь кружок к, а кружку б только – только кружок К. Отметим эти соответствия черными линиями:
еперь из чертежа видно, что кружку Ч может соответствовать лишь кружок к, а кружку б только – только кружок К. Отметим эти соответствия черными линиями:
Теперь становится ясным, что кружок Б может соответствовать только кружку ч:
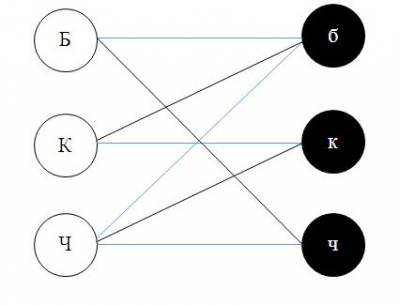
Следовательно, Белов одет в чёрную рубашку, Чернов одет в красную рубашку и Краснов – в белую.
МЕТОД КРУГОВ ЭЙЛЕРА.
Метод кругов Эйлера является еще одним наглядным и довольно интересным способом решения логических задач. В основе этого метода лежит построение знаменитых кругов Эйлера, обычно обозначающих какое-либо множество. Разберем пример применения данного метода.
Задача: Все мои подруги выращивают в своих квартирах какие-нибудь растения. У шестерых из них лилии, а у пяти — фиалки. И только у двоих есть и фиалки и лилии. Угадайте, сколько у меня подруг?
Р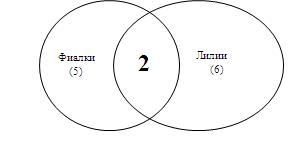 ешение: Итак, мы имеем, что фиалки растут у пяти подруг, а лилии – шести. Условие, что только у двоих есть и фиалки и лилии, позволяет нам применить круги Эйлера:
ешение: Итак, мы имеем, что фиалки растут у пяти подруг, а лилии – шести. Условие, что только у двоих есть и фиалки и лилии, позволяет нам применить круги Эйлера:
СРЕДСТВА АЛГЕБРЫ ЛОГИКИ.
Метод решения логических задач – решение задач средствами алгебры логики становится возможным только после изучения алгебры логики. Поэтому данный метод вызывает некоторые сложности, но на практике находит широкое применение при решении большого круга задач.
МЕТОД БЛОК — СХЕМ.
Идея метода: описать последовательность выполнения операций, определить порядок их выполнения и фиксировать состояния.
|
Более систематический подход к решению задач «на переливание» заключается в использовании блок-схем. Суть этого метода состоит в следующем. Сначала выделяются операции, которые позволяют нам точно отмерять жидкость. Эти операции называются командами. Затем устанавливается последовательность выполнения выделенных команд. Эта последовательность оформляется в виде схемы. Подобные схемы называются блок-схемами и широко используются в программировании. Составленная блок-схема является программой, выполнение которой может привести нас к решению поставленной задачи. Для этого достаточно отмечать, какие количества жидкости удается получить при работе составленной программы. При этом обычно заполняют отдельную таблицу, в которую заносят количество жидкости в каждом из имеющихся сосудов.
| |
|
Задача 6. Имеются два сосуда — трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду.
|
|
|
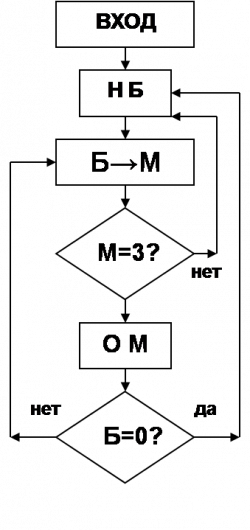
|
Решение. Перечислим все возможные операции, которые могут быть использованы нами, и введем для них следующие сокращенные обозначения: НБ — наполнить больший сосуд водой из-под крана; НМ — наполнить меньший сосуд водой из-под крана; ОБ — опорожнить больший сосуд, вылив воду в раковину; ОМ — опорожнить меньший сосуд, вылив воду в раковину; Б→М — перелить из большего в меньший, пока больший сосуд не опустеет или меньший сосуд не наполнится; М→Б — перелить из меньшего в больший, пока меньший сосуд не опустеет или больший сосуд не наполнится. Выделим среди перечисленных команд только три: НБ, Б→М, ОМ. Кроме этих трех команд рассмотрим еще две вспомогательные команды: Б = 0 ? — посмотреть, пуст ли больший сосуд; М = З ? — посмотреть, наполнен ли малый сосуд.
В зависимости от результатов этого осмотра мы переходим к выполнению следующей команды по одному из двух ключей — «да» или «нет». Такие команды в программировании принято называть командами «условного перехода» и изображать в блок-схемах в виде ромбика с двумя ключами-выходами.
Договоримся теперь о последовательности выполнения выделенных команд. После Б→М будем выполнять ОМ всякий раз, как меньший сосуд оказывается наполненным, и НБ всякий раз, как больший сосуд будет опорожнен. Последовательность команд изобразим в виде блок-схемы (Рис. 1). Начнем выполнение программы. Будем фиксировать, как меняется количество воды в сосудах, если действовать по приведенной схеме. Результаты оформим в виде таблицы
|
|
|

Дальше эта последовательность будет полностью повторяться. Из таблицы видим, что количество воды в обоих сосудах вместе образует следующую последовательность: 0, 5, 2, 7, 4, 1, 6, 3, 0 и т.д. Таким образом, действуя по приведенной схеме, можно отмерить любое количество литров от 1 до 7. Чтобы отмерить еще и 8 литров, надо наполнить оба сосуда.
|
|
|
Задача 7. Среди четырех монет одна фальшивая. Она отличается массой, однако неизвестно, легче она или тяжелее. Масса настоящей монеты 5 г. Как при помощи двух взвешиваний на чашечных весах обнаружить фальшивую монету, если имеется одна гиря массой 5 г? Можно ли при этих условиях опознать, легче фальшивая монета или тяжелее?
|
|
|
|
Решение. Пусть m1, m2, m3, m4 – массы четырех монет соответственно, Г — масса гири. Оформим решение в виде блок-схемы (см. рис.). Приведенная схема задает программу, осуществление которой позволяет установить фальшивую монету и определить, легче она или тяжелее. Взвешиваниям в блок-схеме соответствуют прямоугольники — операторы условного перехода. В схеме выделены первое и второе взвешивания горизонтальными линиями.
|
|
| 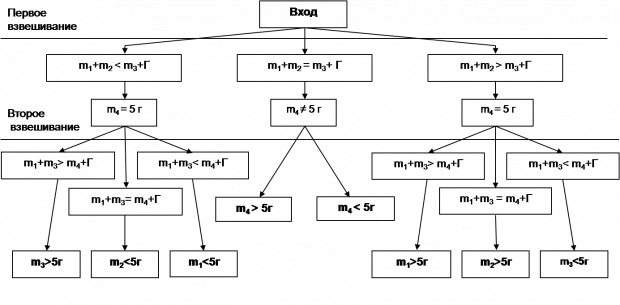
Прокомментируем для примера ход рассуждений, двигаясь лишь по одной ветви блок-схемы. Итак, первое взвешивание: пусть m1 + m2 < m3 + + Г. Это означает, что фальшивая монета находится среди первых трех монет, и, следовательно, четвертая монета истинная, то есть m4 = 5.
Второе взвешивание: пусть m1+m3 > m4+Г. Тогда фальшивая монета тяжелее (так как m4+Г — вес двух истинных монет) и это либо первая, либо третья монета. Но показания весов при первом взвешивании (m1+m2 < m3+Г) позволяют нам сделать вывод, что более тяжелой является третья монета. Если бы показания весов при втором взвешивании были противоположными, то фальшивая монета должна бы быть более легкой, а, стало быть, это была первая монета. Наконец, если при втором взвешивании весы будут в равновесии, то и третья и первая монеты не могут быть фальшивыми. Следовательно, фальшивой является вторая монета и вес ее меньше 5 грамм.
|
МЕТОД МАТЕМАТИЧЕСКОГО БИЛЬЯРДА.
Идея метода: нарисовать бильярдный стол и изобразить действия движениями бильярдного шара, фиксируя состояния в таблице.
Надеемся, что Вам известна игра бильярд за прямоугольным столом с лузами. Появившись до нашей эры в Индии и Китае, бильярд через много веков перекочевал в европейские страны – упоминание о нем имеется в английских летописях VI века. В России бильярд стал известен и распространился при Петре I.
Надеемся, что Вам известна игра
Подобно тому, как азартная игра в кости вызвала к жизни «исчисление» вероятностей, игра в бильярд послужила предметом серьезных научных исследований по механике и математике. Представьте себе горизонтальный бильярдный стол произвольной формы, но без луз. По этому столу без трения движется точечный шар, абсолютно упруго отражаясь от бортов стола. Спрашивается, какой может быть траектория этого шарика? Поиски ответа на этот вопрос и послужили появлению теории математического бильярда или теории траекторий.
|
Задачи на переливание жидкостей можно очень легко решать, вычерчивая бильярдную траекторию шара, отражающегося от бортов стола, имеющего форму параллелограмма. Рассмотрим туже задачу, что и в предыдущем разделе (Метод блок-схем).
Задача 8. Имеются два сосуда — трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду.
|
|

|
Решение. В рассматриваемой задаче стороны параллелограмма должны иметь длины 3 и 5 единиц. По горизонтали будем откладывать количество воды в литрах в 5-литровом сосуде, а по вертикали – в 3-литровом сосуде. На всем параллелограмме нанесена сетка из одинаковых равносторонних треугольников (см. рис.1)
|
|
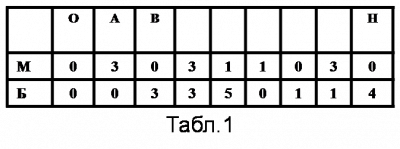
|
|
Бильярдный шар может перемещаться только вдоль прямых, образующих сетку на параллелограмме. После удара о стороны параллелограмма шар отражается и продолжает движение вдоль выходящего из точки борта, где произошло соударение. При этом каждая точка параллелограмма, в которой происходит соударение, полностью характеризует, сколько воды находится в каждом из сосудов.
Пусть шар находится в левом нижнем углу и после удара начнет перемещаться вверх вдоль левой боковой стороны параллелограмма до тех пор, пока не достигнет верхней стороны в точке А. Это означает, что мы полностью наполнили водой малый сосуд. Отразившись упруго, шар покатится вправо вниз и ударится о нижний борт в точке В, координаты которой 3 по горизонтали и 0 по вертикали. Это означает, что в большом сосуде 3 литра воды, а в малом сосуде воды нет, то есть мы перелили воду из малого сосуда в большой сосуд.
Прослеживая дальнейший путь шара, и записывая все этапы его движения в виде отдельной таблицы (табл.1), в конце концов, мы попадаем в точку Н, которая соответствует состоянию, когда малый сосуд пуст, а в большом сосуде 4 литра воды. Таким образом, получен ответ и указана последовательность переливаний, позволяющих отмерить 4 литра воды. Все 8 переливаний изображены схематически в таблице.
Является ли это решение самым коротким? Нет, существует второй путь, когда воду сначала наливают в пятилитровый сосуд. Если на диаграмме шар из точки О покатится вправо по нижней стороне параллелограмма и затем, отразившись от правой боковой стороны, в точку 2 на верхней стороне параллелограмма и т.д., то получим более короткое решение задачи. Можно показать, что полученное решение с 6 переливаниями уже является самым коротким.
|
Есть и другие методы решения логических задач, но они используются реже, чем рассмотренные выше. Выбор метода решения не влияет на ответ задачи, и зависит только от ваших предпочтений и возможностей.

 з второго условия (цвет рубашки не соответствует фамилии) следует, что Б не соответствует б, К – к и Б – б:
з второго условия (цвет рубашки не соответствует фамилии) следует, что Б не соответствует б, К – к и Б – б: еперь из чертежа видно, что кружку Ч может соответствовать лишь кружок к, а кружку б только – только кружок К. Отметим эти соответствия черными линиями:
еперь из чертежа видно, что кружку Ч может соответствовать лишь кружок к, а кружку б только – только кружок К. Отметим эти соответствия черными линиями: 
 ешение: Итак, мы имеем, что фиалки растут у пяти подруг, а лилии – шести. Условие, что только у двоих есть и фиалки и лилии, позволяет нам применить круги Эйлера:
ешение: Итак, мы имеем, что фиалки растут у пяти подруг, а лилии – шести. Условие, что только у двоих есть и фиалки и лилии, позволяет нам применить круги Эйлера: