Конспект урока по математике «Графический способ решения систем уравнений» 9 класс

Урок алгебры по теме

«Графический способ решения систем

уравнений»

Автор: Гаврилова Ирина Николаевна

Учитель математики МОУ « Средняя

общеобразовательная школа №3

г.Козьмодемьянска»

Урок алгебры по теме

«Графический способ решения систем

уравнений».

Цели:

— рассмотреть графический способ решения систем уравнений;

— формировать умение определять по заданному уравнению вид его графика;

— отработать умения и навыки построения графиков;

— прививать аккуратность;

— развивать навыки точного и эстетического построения чертежей и их описания.

Тип урока: объяснение нового материала с использованием мультимедиа технологий.

Программное обеспечение : интерактивная доска, теоретические и практические материалы на электронных носителях, программа графопостроитель «Интерактивная математика», карточки с заданиями.

Ход урока:

1.Организационный момент.

Приветствие учителя.

Вступительное слово.

Я рада вас всех видеть сегодня на уроке.

На предыдущих уроках алгебры мы с вами решали системы уравнений различными способами. Какие способы вы знаете? (Подстановки, алгебраического сложения, замена, графический способ).

2. Проверка Д.З.

Дома вы решали системы уравнений различными способами. Проверим решение системы с параметром способом подстановки.

Решение проецируется через проектор на доску. Учащиеся сверяют решения.

Ответ а= ±2

Сегодняшний урок мы посвятим графическому способу решения уравнений. Данный способ нам знаком с 7 класса, но ежегодно мы изучаем все новые функции, строим их графики, тем самым увеличиваю области применения графического способа при решении систем уравнений.

Наша цель:

— рассмотреть графический способ решения систем уравнений;

— отработать умения и навыки построения графиков;

2. Устная работа: Определите, что представляет собой график уравнения.

3. Изучение темы урока:

1) Решите уравнение

Один учащийся выполняет построение на интерактивной доске, остальные решают уравнение в тетрадях. Корень данного уравнения 1. Выполним устно проверку, подставив корень в данное уравнение.

Есть ли другие способы решения уравнения ? (Это иррациональное уравнение, для решения возводят обе части уравнения в квадрат и выполняют проверку)

2) Решите систему
Первый график- парабола. Координата вершины

(-3;4). Для составления таблицы к этому графику воспользуемся приложением Excel.Второй график гипербола, расположенная в 1 и 2 четвертях.

Учащиеся заполняю таблицу в Excel. Выполняют построение графиков функций в тетради. Находят точки пересечения графиков. Ответ (-3;4) и (-4;3).

3) Работа в парах на ПК с использованием интерактивной лаборатории «Интерактивная математика»

Для решения данной системы преобразуем первое уравнение, которое можно привести к виду (х+1)² +у²=4.

Учащиеся выполняют построение графиков с использованием интерактивной лаборатории «Интерактивная математика» или любого другого графопостроителя. Возьмите карточки-самооценки и оцените свою работу на данном этапе.

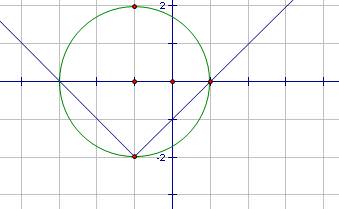
Сколько решений будет иметь система, если во втором уравнении изменить коэффициент 2 на параметр? ( Построение графиков в интерактивных лабораториях дает возможность передвигать график, т.е. решать графически уравнения с параметрами). Данная система может иметь 0,1,2,3,4 решения.

4)Физкультминутка.

1) Верно ли, что при а=10 система не имеет решения?

2) Верно ли, что при а=0 система имеет 3 решения?

3) Верно ли, что при а=-2 система имеет 3 решения?

4) Верно ли, что система может иметь 4 решения?

5)Решение систем уравнений с параметром.

4. Индивидуальная работа по карточкам.

Возьмите карточки-самооценки и оцените свою работу на данном этапе.

5 Домашнее задание.

6. Итоги урока. Оценки за урок.

Какую цель ставили перед собой на уроке?

– Смогли ли ее достичь? Докажите.

– Закончите предложение:

– Я узнал, что…

– Я научился…

– Мне интересно…

– А теперь определите свои проблемы и зафиксируйте в карточке-самооценки.

– Мы с вами были сегодня на уроке полноправными партнёрами. И оценка вашей деятельности, не отметка, а оценка – отлично.

Итак, мы сегодня рассмотрели применение графического способа решения систем уравнений. Несмотря на то, что графический способ имеет свои недостатки (неточность нахождения корней, возможность применения только для тех функций, графики которых мы можем построить), но его удобно применять при решении систем с параметром, систем, для которых алгебраические решения сложны и громоздки.

“Математика во всем”, — нам твердят.
Многие не верят, спорить норовят:
“Математика от нас далеко…
Жить на свете без нее так легко!..”

Но пойдет однажды вечером дождь.
Подойдешь ты к окну и поймешь:
Все на свете, что видишь, давно
Математикой отражено.

Ты вглядись: от фонаря свет
Векторами отражается. Нет?
Точки капель, окружности луж – 
Неужели ты не видишь? Ну уж…

Окошек плоскости отрезками полны…
И вечна траектория Луны…
А по параболе летит метеорит.
Через мгновенье в атмосфере он сгорит…

Многоугольники, квадраты и круги…
Пространства-времени неслышные шаги…
Все движется и мчится, все улетает вдаль.
А кто не видит этого… 
                           того мне просто жаль.
                                       Д.Артемова