Тема урока
«Логарифмическая функция и её приложения»
Цель урока: * расширить представление учащихся о логарифмической
функции, применении её свойств в нестандартных
ситуациях.
Метод урока: создание ситуации выбора и успеха.
Принцип (урока) – творчества и успеха.
Основное понятие – самовыражение.
Ход урока.
1.Сообщение учащихся по темам.
1) Ода экспоненте.
2) Логарифмы в музыке.
3) Звезды, шум и логарифмы.
4) Дополнение учителя.
5) «Любое число – тремя двойками»
2. Конкурс знатоков логарифмической функции.
Потому – то , словно пена
Опадают наши рифмы.
И величие степенно
Отступает в логарифмы.
Борис Слуцкий.
(эти строки записаны на доске)
Ода экспоненте.
По истине безграничны приложения показательной и логарифмической функций в самых различных областях науки и техники, а ведь придумывали логарифмы для облегчения вычислений. Более трёх столетий прошло с того дня, как в 1614 году были опубликованы первые логарифмические таблицы, составленные Джоном Непером. они помогали астрономам и инженерам, сокращая время на вычисления. Ещё недавно трудно было представить без логарифмической линейки в кармане. Изобретённая через десяток лет после появления логарифмов Непера английским математиком Гунтером, она позволяла быстро получать ответ с достаточной для инженера точностью в три значащие цифры. Теперь её вытеснили микрокалькуляторы, но без логарифмической линейки не были бы построены ни первые компьютеры, ни калькуляторы.
Многообразные применения показательной ( или экспоненциальной как ещё её называют) функции вдохновили английского поэта Эллера Брилла, он написал «Оду экспоненте».
… «Ею порождено многое из того,
Что достойно упоминанию».
Как говорили наши
Англосаксонские предки,
Могущество её порождений
Заранее обусловлено её
Общественной красотой и силой,
Ибо они суть физическое воплощение
Абстрактной идеи её.
Английские моряки любят и знают её
Под именем «Гунтер».
Две шкалы Гунтера
Вот чудо изобретательности.
Экспонентой порождена
Логарифмическая линейка:
У инженера и астронома не было
Инструмента полезнее, чем она.
2) Логарифмы в музыке.
… «Даже изящные искусства питаются ею.
Разве музыкальная гамма не есть
Набор передовых логарифмов?»
( из «Оды экспоненте»)
Музыканты редко увлекаются математикой; большинство из них питают к этой науке чувство уважения. Между тем, музыканты – даже те, которые не проверяют подобно Сальери у Пушкина «алгеброй гармонию» — встречаются с математикой гораздо чаще, чем сами подозревают, и притом с такими «страшными» вещами, как логарифмы.
И действительно, так называемые ступени темперированной хроматической гаммы (12 звуковой) частот звуковых колебаний представляют собой логарифмы. Только основание этих логарифмов равно 2 (а не 10, как принято в других случаях).
Положим, что ноте «до» самой низкой октавы – будем её называть нулевой – соответствует частота равная n колебаний в секунду. В октаве частота колебаний нижнего звука в 2 раза меньше верхнего, т.е. эти частоты соотносятся как 1 : 2. Тогда ноте «до» первой октавы будут соответствовать 2n колебания в секунду, а ноте «до» третьей октавы – n*2m колебания в секунду и т. д. Обозначим все ноты хроматической гаммы номерами р. Тогда высоту, т.е. частоту, любого звука можно выразить формулой
N = n*2m+p/12 — ( в гамме 12 нот, m — номер октавы, p/12 — номер ноты)
Npm=n*2m(12√2)p
lgNpm= lgn + m lg2 + p*lg2
12
lgNpm= lgn + (m+p/12)lg2
Принимая частоту самого низкого «до» за единицу (n = 1) и приведя все логарифмы к основанию 2, имеем
log2Npm= m + p/12 log2Npm = log2n + (m + p/12)*log22 ;
log210 log210 log210
log2Npm = 0 + (m + p/12) *__1__
log210 log210
3) Звёзды, шум и логарифмы.
Громкость шума и яркость звёзд оцениваются одинаковым образом – по логарифмической шкале.
Астрономы делят звёзды по степени яркости на видимые и абсолютные звёздные величины – звёзды первой величины, второй, третьей и т. д. Последовательность видимых звёздных величин, воспринимаемых глазом, представляет собой арифметическую прогрессию. Но физическая их яркость изменяется по иному закону: яркости звёзд составляют геометрическую прогрессию со знаменателем 2,5. Легко понять, что «величина» звезды представляет собой логарифм её физической яркости. Короче говоря, оценивая яркость звёзд, астроном оперирует таблицей логарифмов, составленной при основании 2,5.
Вредное влияние промышленных шумов на здоровье рабочих и на производительность труда побудило выработать приёмы точной числовой оценки громкости шума. Единица громкости звука — «бел», но практически используются единицы, равные его десятой доле — «децибелы». Последовательные степени громкости 1 бел, 2 бела и т.д. составляют арифметическую прогрессию.
Физические же величины, характеризующие шумы (энергия, интенсивность звука и т.д.) составляют геометрическую прогрессию со знаменателем 10. Громкость, выраженная в белах, равна десятичному логарифму соответствующей физической величины.
4) Дополнение учителя.
Ощущения, воспринимаемые органами чувств человека, могут вызываться раздражениями, отличающимися друг от друга во много миллионов и даже миллиардов раз. Удары молота о скользкую плиту в 100 раз громче, чем тихий шелест листьев, а яркость вольтовой дуги в триллионы раз превосходит яркость какой-нибудь слабой звезды, едва видимой на ночном небе. Но никакие физиологические процессы не позволяют дать такого диапазона ощущений. Опыты показали, что организм как бы «логарифмирует» полученные им раздражения, т.е. величина ощущения приблизительно пропорциональна десятичному логарифму величины раздражения.
Как видим, логарифмы вторгаются и в область психологии.
5) Любое число — тремя двойками.
Продолжим урок остроумной алгебраической головоломкой, которой развлекались участники одного съезда физиков в Одессе. Предлагается задача:
-5-
любое данное число, целое и положительное, изобразить с помощью трёх двоек и математических символов.
Например, пусть дано число 3.
Решение: 3 = — log2log2√√√2 , так как √√√2 = 21/8 , log(21/8) = 1/8log22 = 1/8,
— log21/8 = — (- 3) = 3.
Аналогично 5 = —log2log2√√√√√2 .
Общее решение задачи записывается в виде
N = — log2log2√√√….√2 .
N раз
2. Конкурс знатоков логарифмической функции.
Класс разбит на несколько команд.
Разминка.
Какая команда первой правильно назовёт ответ, та и начинает конкурс.
Вычислите log15225 = 2
log1/88 = — 3
log3√100 = 2/3
32log32 = 4
log2log381 = 2.
2. Определение логарифма, основное логарифмическое тождество.
log64 + log69 = [log636 = 2]
log1/24 + log3 1/(3√3) = [ — 2 + log33-1.5 = — 2 – 1,5 = — 3,5]
– log9log28 – 4log40,5 = [-1/2 –1/2 = -1]
3. Свойства логарифмической функции.
1. Найти D(у), если у = log2(3x – 2).
D(y): 3x – 2 > 0, 3x > 2, x > 2/3 D9y) = (2/3 ;+∞)
2. Сравнить числа 1; log1/38; log35; log1/39.
log1/39 < log1/38 < 1 < log35.

3. Найти область значений функции у = log2(4 – 5x), если х € [ — 4/5; 0].
D(y): 4 – 5x > 0, -5x > — 4, x < 4/5 D(y) = (-∞; 4/5)
y(-4/5)= log2(4 – 5*(-4/5))= log28 = 3
y(0) =log2(4 –5*0) = log24 =2
E(y) = [2; 3].
4. Логарифмические уравнения.
1. log1/3(3x – 5) = — 2 [x = 3]
2. log32x – log3x = 2 log3x = 2 x = 9
log3x = — 1 x = 1/3.
3.log7(2x – 3) = log7(x – 2)
2x – 3 > 0 2 – 3 >0 ложно
х – 2 >0 1 – 2 > 0 ложно => Ø
2x – 3 = x – 2 x = 1
-7-
5. График функции.
1.Построить график функции у =(x2)logx² | x |
y = | x |, x ≠ 0, x ≠ ±1
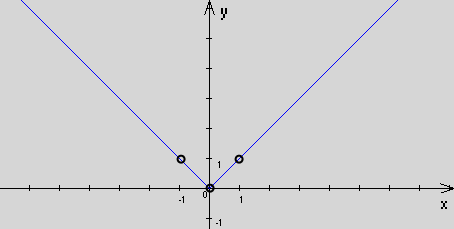
2. y = 10lgx² + log3 – x(3 – x)
x
y = x + 1, x < 3, x ≠ 0 ; x ≠ 2

— 7 —
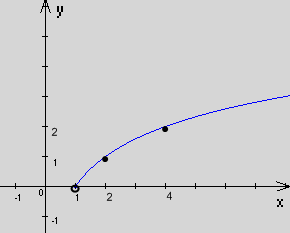
3. y = 2log2(log2x)
D(y): log2x > 0, => x > 1
y = log2x
Разработка Ахтямовой Г.Г.
