Цели:
— образовательные:
обобщить и систематизировать знания по данной теме;
повторить и закрепить умения:
преобразовывать графики тригонометрических функции;
графически решать уравнения,
познакомить с графиками y = │sin x│ и y = sin│x│,
— развивающие: развивать устную и письменную математическую речь, графическую культуру, умения аргументировать свои ответы.
— воспитательные: формировать такие качества личности, как трудолюбие, организованность, активность и самостоятельность в выборе способа решения
Оборудование урока: компьютеры, проектор, интерактивная доска
План урока
Организационный момент.
Ребята, сегодня у нас тема урока: «Преобразования графиков тригонометрических функций».
II. Проверка домашнего задания . Проверим домашнее задание в электроном виде. Свои слайды показывают ученики.
а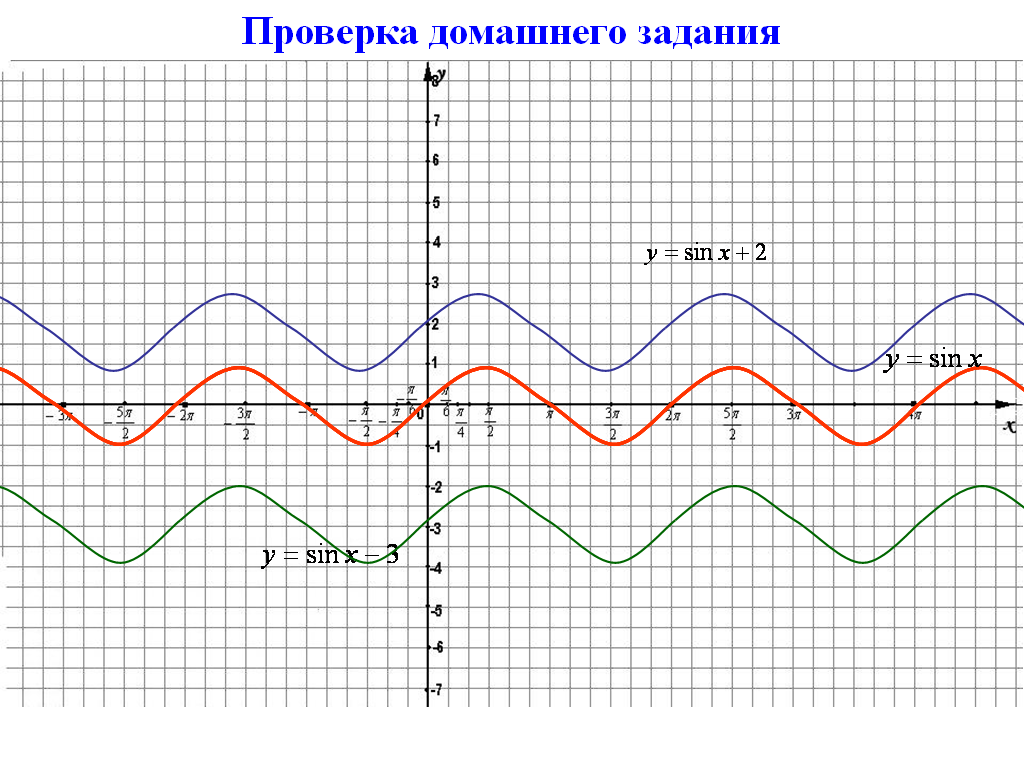 ) Параллельный перенос вдоль оси OY
) Параллельный перенос вдоль оси OY
Например:
а) y = sin x + 2;
б) y = sin x -3;
б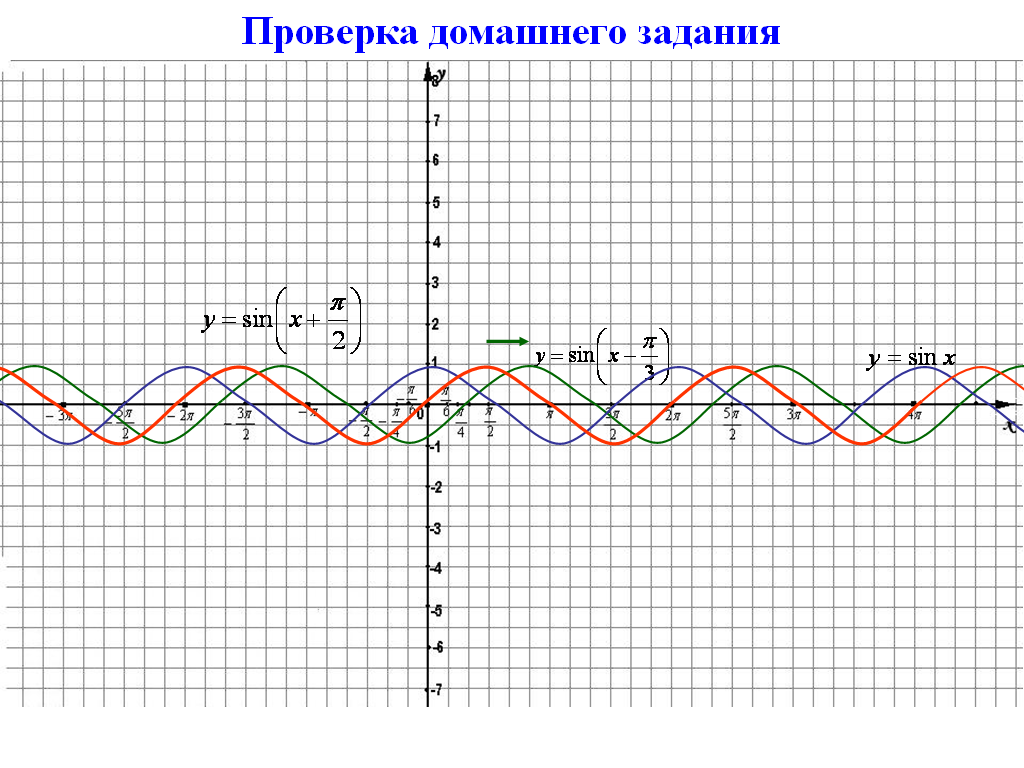 ) Параллельный перенос вдоль оси OX
) Параллельный перенос вдоль оси OX
Например:
![]()
![]() а)
а)
б![]() )
)
в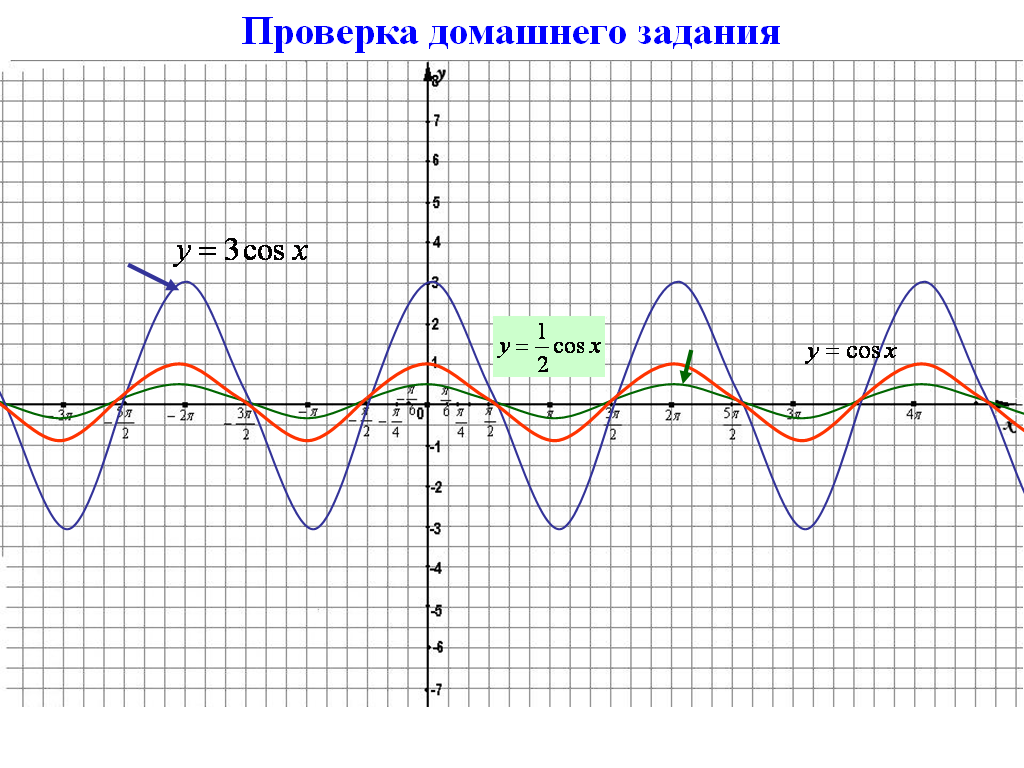 ) Растяжение (сжатие) в k раз вдоль оси OY
) Растяжение (сжатие) в k раз вдоль оси OY
.
Например:
а) y = 1/2 cos х
б) y= 3 cos х
г ) Растяжение (сжатие) в k раз вдоль оси OX
) Растяжение (сжатие) в k раз вдоль оси OX
Например:
а) y = sin (2х)
б) y= sin( х /3)

Ответьте на вопросы:
| Преобразование графика функции y=f(x) | |
| y=f(x)+b | Параллельный перенос его вдоль ОУ на b единиц |
| y=f(x-a) | Параллельный перенос его вдоль ОХ на а единиц |
| y=kf(x) | Растяжение вдоль оси ОУ с коэффициентом k (k>1 растяжение, 0<k<1 сжатие) |
| y=f(kх) | Растяжение вдоль оси ОХ с коэффициентом k (0<k<1 растяжение, k>1 сжатие) |
| y=-f(x) | Симметричное отражение его относительно оси ОХ |
III. Закрепление изученного материала
В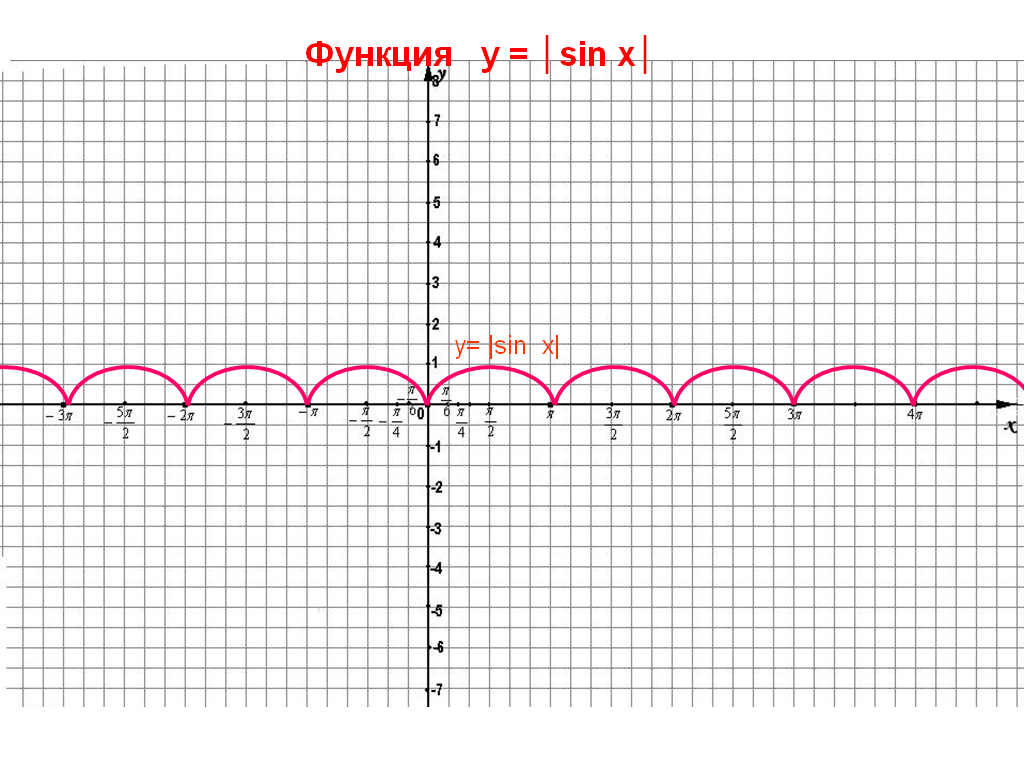 спомним, что такое модуль ? Абсолютной величиной ( или модулем) действительного числа х называется неотрицательное число │ x│, определяемое соотношение
спомним, что такое модуль ? Абсолютной величиной ( или модулем) действительного числа х называется неотрицательное число │ x│, определяемое соотношение
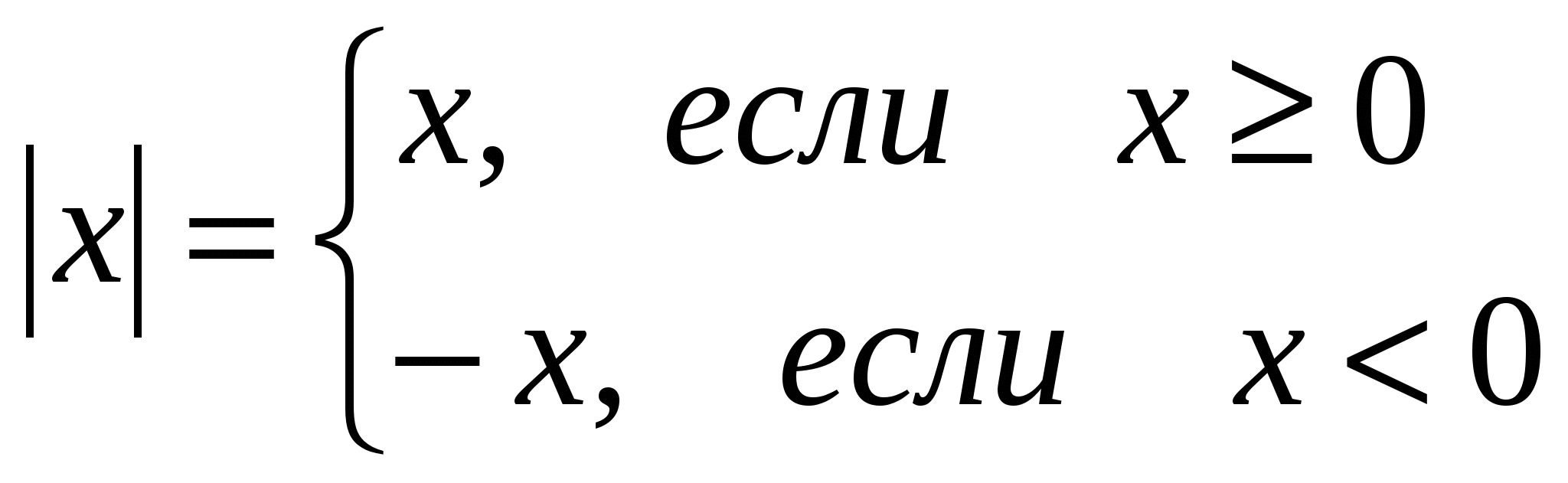
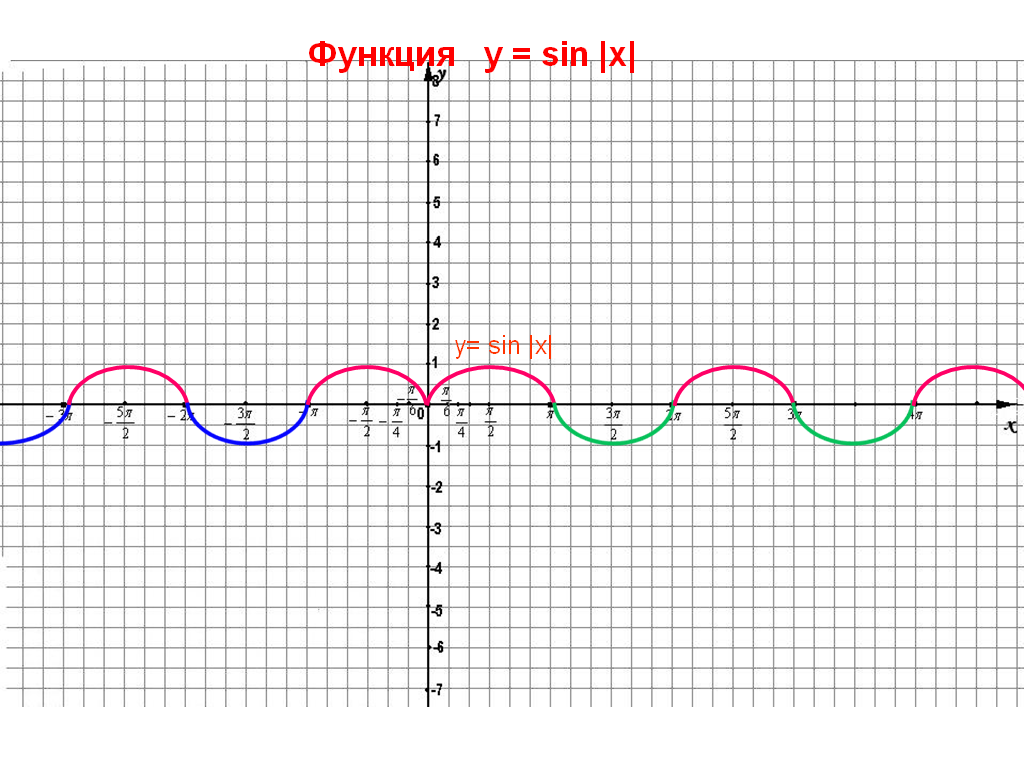
Рассмотрим функцию y = │sin x│. При sinx ≥ 0 график функции y = sinx , а при sinx < 0 график функции y = — sinx следовательно часть функции y = sinx ниже оси у зеркально отобразиться и будет расположена в верхней полуплоскости.
Рассмотрим функцию y = sin│x│ .Чтобы построить график функции y = sin│x│, надо построить сначала график функции y = sinx при х > 0, а затем построить кривую симметричную построенному графику относительно оси ординат.
Если в модуль берется аргумент функции, то график будет симметричен относительно оси ординат.
Если в модуль берется все уравнение, выражающее функцию. То график отражается в верхнюю полуплоскость относительно оси абсцисс. Запишите этот вывод в блокнот с теорией.
Решите уравнение:
10|sinx|=10|cosx|-1 (работа на интерактивной доске)
Решение: Данное уравнение рационально решать графоаналитическим методом.
Т.к. 10>1, то данное уравнение равносильно следующему:
|sinx|=|cosx|-1
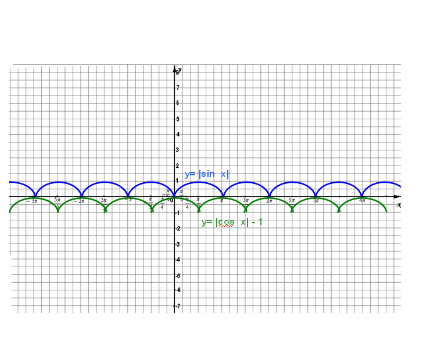
Точки пересечения графиков имеют координаты (пk;0); k €z
Ответ: x = пk; k €z
Решите уравнение:
2cos πx=2x-1
Решение:
Д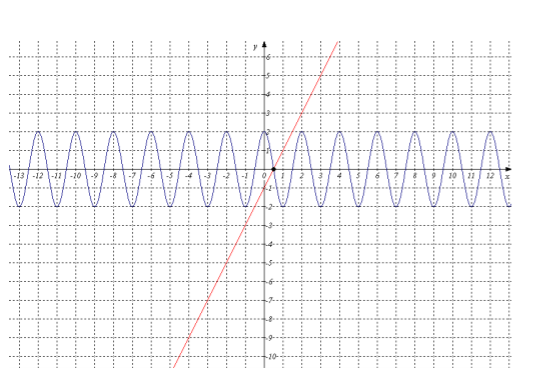 анное уравнение рационально решать графическим методом.
анное уравнение рационально решать графическим методом.
Точка пересечения графиков имеет координаты (0,5; 0). Следовательно, х=0,5
Ответ: х=0,5
В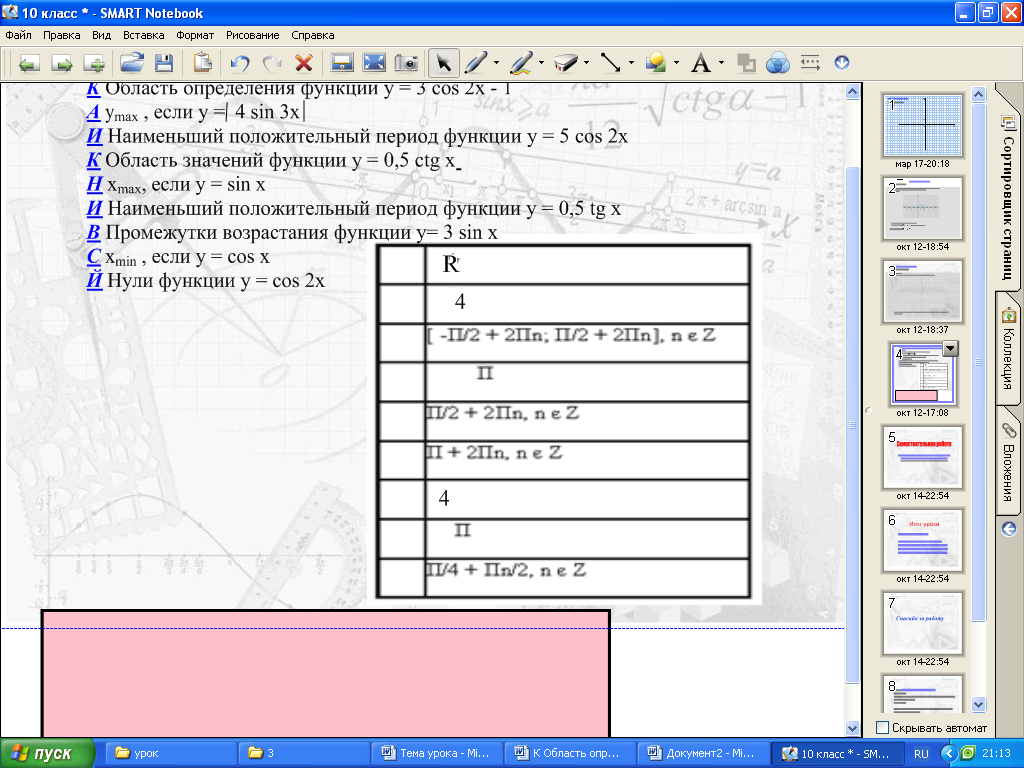 ыполнив следующее задание, вы составите слово.
ыполнив следующее задание, вы составите слово.
Найдите:
К ymax , если y = 4 sin 3x
А Область определения функции y = 3 cos 2x — 1
И Наименьший положительный период функции y = 5 cos 2x
К наибольшее значение функции y = 2 sin x + 2
Н xmax, если y = sin x
И Наименьший положительный нуль функции
y= 3 sin x
В Промежутки возрастания функции y= 3 sin x
С xmin , если y = cos x
Й Нули функции y = cos 2x
Получилось имя философа Фомы Аквинского, который сказал:«Знания — столь драгоценная вещь, что их не зазорно добывать из любого источника«
III . Самостоятельная работа учащихся. Работа за компьютерами, где ставится оценки за работу.
Вариант 1
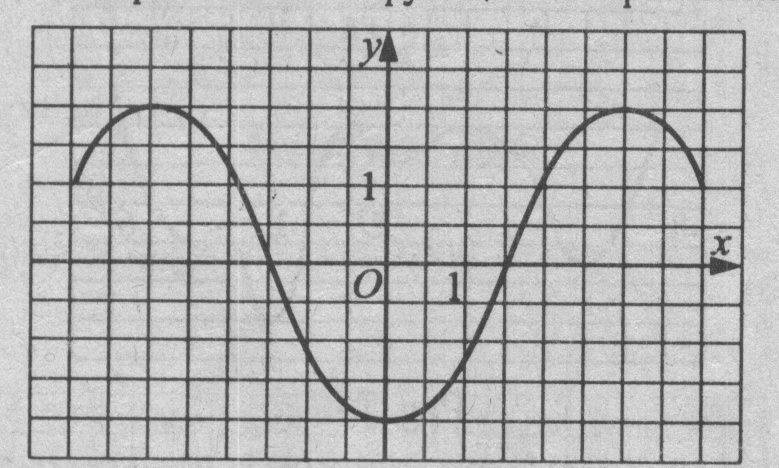
График какой из перечисленных функций изображён на рисунке
![]()
![]()
![]()
4. ![]() 2. Найдите множество значений функции
2. Найдите множество значений функции ![]()
( 2; 3 )
[ 1; 5 ]
( 1; 5 )
[ 2; 3 ]
3. Найдите период функции ![]() в градусах.
в градусах.
4. Найдите наименьшее положительное значение а , при котором период функции
![]() равен 4π.
равен 4π.
5. Решите уравнение ![]()
Вариант 2
Укажите график функции, заданной формулой ![]()

2. Найдите множество значений функции ![]()
1.[ 1; 4 ]
2.( 3; 4 )
3.[ -5; -1 ]
4.( -7; -6)
3. Найдите период функции ![]() в градусах.
в градусах.
4. Найдите наименьшее положительное значение а , при котором период функции
![]() равен 8π.
равен 8π.
5. Решите уравнение ![]() IV . Подводится итог урока. Продолжите фразу:
IV . Подводится итог урока. Продолжите фразу:
“Сегодня на уроке я узнал…”
“Сегодня на уроке я научился…”
“Сегодня на уроке я повторил…”
“Сегодня на уроке я закрепил…”
В конце урока я хочу вам рассказать притчу. Шёл мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил: «Что ты делал целый день?». И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?», и тот ответил: «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительства храма». Ребята! Давайте оценим каждый свою работу за урок.. Кто работал, как первый человек, покажите круг синего цвета; кто работал добросовестно, зелёного; кто принимал участие в строительстве храма — красного.
Спасибо за работу. V . Домашнее задание 1 группа Постройте графики функций: y = │соs x│- 3 , y = соs x │x│+ 3. №11.9 (г)
2 группа Постройте графики функций: │у│= sin х, │у│= соs x + 3. № 11.10
