Хостинг документов » Конспект урока по Математике «Простейшие тригонометрические уравнения» 10 класс

Конспект урока по Математике «Простейшие тригонометрические уравнения» 10 класс

Разработка урока в 10 классе

Тема урока: Простейшие тригонометрические уравнения

Цель урока:

Образовательные:

— актуализировать знания учащихся по теме «Решение тригонометрических уравнений» и обеспечить их применение при решении задач вариантов ЕГЭ;

— рассмотреть общие подходы решения тригонометрических уравнений;

— закрепить навыки решения тригонометрических уравнений;

— познакомить с новыми способами решения тригонометрических уравнений.

Развивающие:

— содействовать развитию у учащихся мыслительных операций: умение анализировать, синтезировать, сравнивать;

— формировать и развивать общеучебные умения и навыки: обобщение, поиск способов решения;

— отрабатывать навыки самооценивания знаний и умений, выбора задания, соответствующего их уровню развития.

Воспитательные:

— вырабатывать внимание, самостоятельность при работе на уроке;

— способствовать формированию активности и настойчивости, максимальной работоспособности.

Ход урока

Организационный момент
Контрольные вопросы

Решения простейших тригонометрических уравнений.
Два основных метода решения тригонометрических уравнений.
Определение однородного тригонометрического уравнения первой и второй степеней.
Решение однородного тригонометрического уравнения первой степени.
Алгоритм решения однородного тригонометрического уравнения второй степени.

Выполнение теста по вариантам

Тест

Тема: Тригонометрические уравнения.

1 вариант

1. Уравнение sin x –3 cos x = 0 решается методом:

а) введения новой переменной;

б) разложения на множители;

в) деления обеих частей уравнения на cosx;

г) деления обеих частей уравнения на cos²x.

Эталон: в.

2. Решением уравнения cos²x–cos x–2=0 являются:

а) х=2k, k;

б) х=+k, k;

в) х=arccos 2+2k, х=+2k, k;

г) x=+2k, k.

Эталон: г.

Решением уравнения 3cos²x=sin x cos x являются:

а) х=arctg 3+k, k;

б) х=+k, x=arctg 3+k, k;

в) х=+2k, х=arctg 3+k, k;

г) x=arctg 3+k, k.

Эталон: б.

4. Наименьший положительный корень уравнения sin 2x=cos 2x равен:

а) ;

б) ;

в) ;

г) .

Эталон: в.

2 вариант

1. Уравнение 3sin x cos x–2cos x=0 решается методом:

а) введения новой переменной;

б) разложения на множители;

в) деления обеих частей уравнения на cosx;

г) деления обеих частей уравнения на cos²x.

Эталон: б.

2. ешением уравнения sin²x–2sin x cos x+cos²x=0 являются:

а) х=+k, k;

б) х=+k, k;

в) х=+2k, k;

г) х=-+k, k.

Эталон: б.

3. Решением уравнения — sin²x=sin x cos x являются:

а) х=k, х=-+2k, k;

б) х=k, х=+k, k;

в) х=k, х=-+k, k;

г) x=-+k, k.

Эталон: в.

Наименьший отрицательный корень уравнения sin=cos равен:

а) —;

б) -2;

в) —;

г) —.

Эталон: б.

Решение уравнений

Работа по отработке умений решать тригонометрические уравнения (письменная работа у доски и в тетрадях)

а) Решим уравнение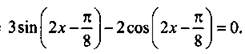

Решение:

Разделим все члены уравнения на и получим: Найдем и

б) Решим уравнение

Решение:

Учтем четность функции косинуса и формулы приведения. Получим: или Разделим обе части уравнения на cos 3x. Имеем: 2tg 3x = -1, откуда tg 3x = -1/2,

в) Решим уравнение

Решение: Разложим левую часть уравнения на множители: Произведение двух множителей равно нулю. Поэтому один из множителей равен нулю. Получаем простейшее тригонометрическое уравнение cos х = 0 (его решения ) и однородное тригонометрическое уравнение первого порядка или (его решения ).