Хостинг документов » Конспект урока по Математике «Золотое сечение в математике, архитектуре, скульптуре и музыке» 10 класс

Конспект урока по Математике «Золотое сечение в математике, архитектуре, скульптуре и музыке» 10 класс

Урок математики «Золотое сечение в математике,

архитектуре, скульптуре и музыке»

Выполнила:

Сосновцева Татьяна Петровна

Учитель математики

МОУ «Средняя общеобразовательная школа № 1 р. п. Новые Бурасы Новобурасского района Саратовской области»

2009г.

Класс: 10

Тема: Золотое сечение в математике , архитектуре, скульптуре и музыке

Тип урока: закрепления и совершенствования знаний умений и навыков.

Класс: обычной общеобразовательной школы.

Цели урока (образовательные, развивающие, воспитательные).

В ходе урока учащиеся научатся:

— формулировать основные свойства золотого сечения

— применять полученные знания к решению задач

— решать задачи с применением полученных знаний на уроке

— ставить и решать проблемы;

— анализировать данные и результаты;

— формулировать выводы;

— работать в группе;

— публично выступать;

— выражать собственное мнение;

— самостоятельно выполнять практические работы;

— оценивать свой результат;

— давать рекомендации.

Оборудование: мультимедийный проектор, экран, ПК, презентация к уроку. На столах учеников раздаточный материал – карточки для проведения практических работ.

Ход урока:

Организационный момент:

Девиз урока

Слайд 2.

Организационный момент.

Ребята, сегодня мы познакомимся с вами с понятием «золотое сечение».

Девизом нашего урока будут слова: «Нет ни искусства без упражнений, ни упражнений без искусства»

Актуализация знаний.

Слайд 3.

«Нет ни искусства без упражнений, ни упражнений без искусства» — это вечная тема. Устройство мира, его гармония — одна из них. Слово «гармония» имеет несколько значений: связь, созвучие, соразмерность, согласованность частей одного целого. Представители многих искусств пытались уловить законы гармонии и использовать их в своих произведениях.

Науки математические с самой глубокой древности обращали на себя особенное внимание, в настоящее время они получили еще больше интереса по влиянию своему на искусство.

Например, архитектура.

Афинский скульптор Фидий (5 век до нашей эры) считал самым гармоничным отношением золотое сечение, которое использовал для возведения величественных греческих храмов.

И среди первое место по праву принадлежит Парфенону.

Парфенон:

Слайд 4.

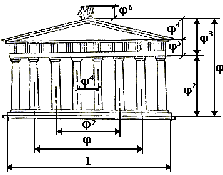
Золотое сечение в пропорциях Парфенона

Это древнее сооружение с его гармоническими пропорциями дарит нам эстетическое наслаждение.

Даже сейчас, когда он стоит в развалинах, Парфенон в Афинах –это одно из самых знаменитых сооружений в мире. Он был построен в эпоху расцвета древнегреческой математики.

Мы видим на рисунке, каким образом фасад Парфенона вписывается в прямоугольник, стороны которого образуют так называемое «золотое сечение.»

Слайд 5.

Золотое сечение – длина прямоугольника больше его ширины в 1,618 раза. Вычислить точно значение нельзя, так как это иррациональная дробь. Греки же умели строить золотые прямоугольники, а на их основе архитектурные сооружения, но не умели находить длины их сторон

Давайте попробуем с вами сейчас построить так называемый золотой прямоугольник.

Практическая работа № 1

«Построение «золотого прямоугольника»»

Прямоугольник.

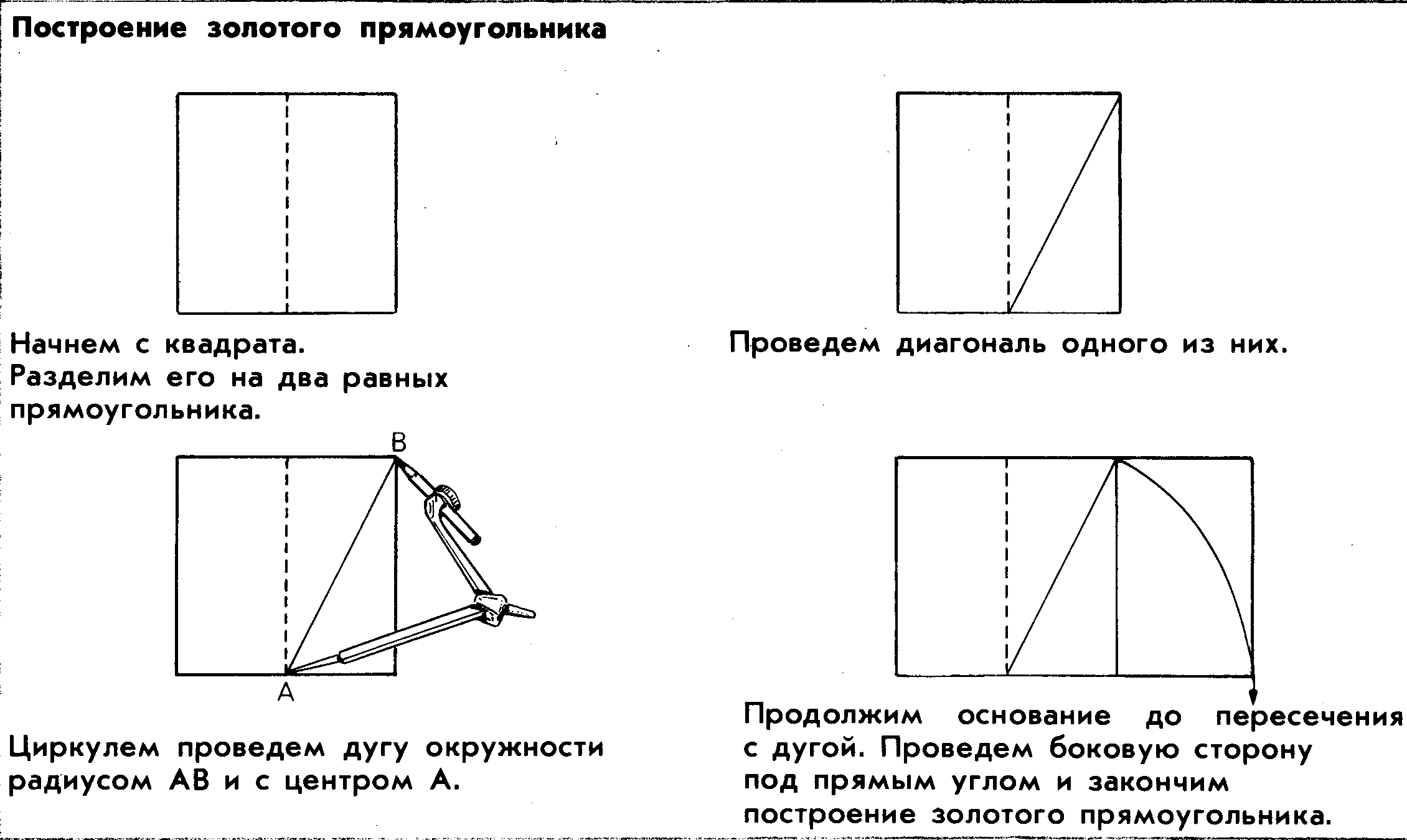
Любой прямоугольник, стороны которого относятся как 1:1,618 называется золотым! И его вы построили.

Молодцы!

Слайд 6.

2. Приведем примеры архитектурных сооружений.

3. Изобразительное искусство.

ПРИСУТСТВИЕ КРАСОТЫ

Ценность науки –математика , определяется не только тем, что она помогает создать материальные блага, среди которых мы живем. Математика формирует и интеллектуальную атмосферу.

Рассмотрим материал, показывающий неразрывную связь

математики и изобразительного искусства.

Начнем с искусства Древнего Египта.

В живописи и скульптуре храмов, на предметах домашнего обихода древние египтяне чаще всего изображали богов и фараонов. Были установлены каноны изображения стоящего человека, идущего, сидящего, коленопреклоненного и т.д. По особым правилам рисовали и священный цветок лотоса, и священных животных.

Канон для изображения человеческой фигуры был разработан путем изучения и измерения как всей фигуры, так и каждой ее части. При этом использовалась такая система пропорционального членения фигуры на части, которая позволяла по части определить целое — и по одной части тела определить размер другой.

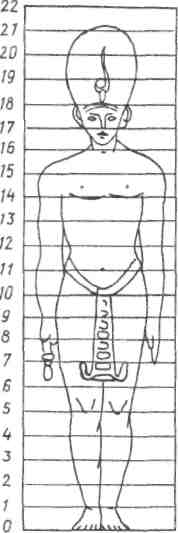
Ученые нашли в Египте рисунок человеческой фигуры, которая была изображена стоящей прямо, лицом вперед, и тело этой фигуры было разделено параллельными горизонтальными линиями на 21 — части (рис. I).

Единицей измерения служила длина среднего пальца руки. Само тело человека разделено на 19 равных частей,

2— части приходятся на традиционный головной убор фараонов.

Учеными позже было установлено, что по египетскому канону фигура человека имела следующие размеры:

Слайд № 7

Высота стопы == длине среднего пальца руки,

Расстояние от коленной чашечки до лобка == длине четырех

Пальцев на руке

Этот канон давал возможность ваятелю при изображении фигуры очень больших размеров (колосса) по величине целого судить о размерах отдельных частей и, наоборот, по размерам какой-либо части—о размере всей фигуры. Известно, что египетские скульпторы лепили колоссов по частям, т.е. каждую часть одной и той же фигуры выполняли несколько мастеров порознь, порой даже в разных местах. Но когда готовые части складывались вместе, то они точно сходились без нарушения пропорций.

Рис. 1

4. СКУЛЬПТУРА

Достижения египтян удивляли и восхищали художников Древней Греции. Они специально совершали путешествия в Египет, чтобы поучиться умению пользоваться каноном.

Греки продолжили и развили традиции египтян в искусстве. Ставя во главу угла образ человека, они наблюдали и изучали человеческое тело во всех деталях. Греческие художники утверждали, что в мире царит всеобщая закономерность, а сущность прекрасного заключается в строгом порядке, в симметрии, в гармонии частей и целого, в правильных математических отношениях.

Одним из высших достижений греческого, да и всего мирового искусства явилось творчество афинского скульптора Фидия (V в. до н.э.). Он присутствовал при реконструкции Акрополя в Афинах. Творчество Фидия оказало влияние на ваятельное искусство всего эллинизма. Его образы, наделенные жизненной достоверностью, свидетельствуют о глубоком изучении реального мира.

Самым гармоничным отношением Фидий считал золотое сечение. Благодарная память о скульпторе до сих пор сохраняется в этом понятии, поскольку числовое значение золотого сечения обозначается через ф по первой букве имени Фидия.

Слайд № 8

ПРАКТИЧЕСКАЯ РАБОТА № 2

Подсчитаем это значение.

Примем длину отрезка, в котором надо найти золотое сечение,

за 1.

Его большую часть обозначим через х, тогда меньшая — это 1-х. По определению золотого сечения составляем уравнение

1-х / х = х / 1

Решив его относитель Х , получим Х = (√ 5 – 1) =0,618…

Это и есть число золотого сечения Ф.

Ф = 0,618.

В работах скульптора золотое сечение заложено в различных пропорциях человеческого тела.

Не только вся статуя, но и отдельные ее части делятся в золотом отношении.

Приведем несколько примеров.

Слайд № 9

5. ИЗГОТОВЛЕНИЕ И РОСПИСЬ СОСУДОВ.

В особый вид изобразительного искусства Древней Греции следует выделить изготовление и роспись всевозможных сосудов. В изящной форме амфор и кратеров, а также в их росписи легко угадываются пропорции золотого сечения (рис. 5). Например, для амфоры на рис. 5, а выполняются

Отношения а/в = с/ д = д л = Ф.

Приведем несколько примеров.

Слайд № 10

Практическая работа №3

А теперь — решим вместе следующую, очень древнюю геометрическую задачу.

Условие задачи читается так:

разделить отрезок в среднем и крайнем отношении.

Другая формулировка:

разделить отрезок гармонически.

Третья формулировка:

найти золотое сечение отрезка.

Этот термин впервые применил великий Леонардо да Винчи (1452—1519).

Пожалуй, во всех этих формулировках условие задачи не совсем понятно. На современном языке оно будет звучать менее выразительно, но более понятно:

разделить данный отрезок на две части так, чтобы меньшая относилась к большей, как большая ко всему отрезку.

Существует много решений задачи. Одно из самых простых и наглядных предложил знаменитый александрийский математик Клавдий Птолемей (ок. 90 — ок. 160), имя которого вам хорошо известно — именно он разработал то учение о строении Солнечной системы, которым пользовались астрономы и мореплаватели до Николая Коперника.

Итак, решаем задачу

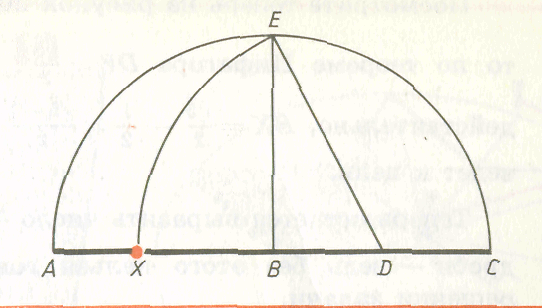
Пусть надо построить золотое сечение отрезка АВ (рис. 20).

С центром в точке В радиусом АВ проводим полуокружность АЕС.
Разделим радиус ВС пополам, получим точку Д.

3.Проведем дугу окружности с центром в точке Д радиусом ДЕ до пересечения с АВ.

4. Точка пересечения Х и есть искомая точка.

Слайд № 11

6. Леонардо да Винчи

Термин «Золотое сечение» ввел Леонардо да Винчи — гениальный живописец, ученый и инженер.

«Он сказал: если мы человеческую фигуру перевяжем поясом и отмерим расстояние от пояса до ступней, то эта величина будет относится к расстоянию от того же пояса до макушки как весь рост человека относится к длине от пояса до ступней т.е.

Т.е математическим языком это выглядит так: 2s:a =M:2s

Эти соотношения он неизменно использовал в своих художественных произведениях.

Слайд № 12

Практическая работа № 4

Выполним практическую работу: 1 ряд измеряет пропорции мужчины, 2 ряд -женщины. (Нужны калькуляторы)

Мы с вами убедились, то не все люди соответствуют правилам золотого сечения. Поэтому не каждый может работать в модельном бизнесе.

Слайд № 13

7. Вернемся к произведениям Леонардо да Винчи.

Посмотрите на Джаконду. Это самая православная картина во всей истории живописи. Написанная почти пять столетий назад она стала сенсацией XX века.

Что есть человек?

Он только частица,

Только атом в громадной природе.

А чем частица может гордиться?

Нечем частице гордиться вроде.

Когда человек творит вдохновенно,

Он в это время один в целом свете,

И в эти часы и в минуты эти

Он равен всей бесконечной

вселенной.

Посмотрим на другие произведения: там, где присутствует золотое сечение — лицо гармонично и привлекательно.

Золотая пропорция отвечает не только делению тела на две неравные части линией талии.

Слайд № 14

Пропорции лица то же тоже подчиняются правилам золотого сечения.

Отношение

Высота лица (до корней волос)

к вертикальному расстоянию между дугами бровей и нижней частью подбородка

= отношению
расстояния между нижней частью носа и нижней частью подбородка

расстоянию между углами губ и нижней частью подбородка .

Это отношение равно золотой пропорции.

Слайд № 15

На экране вы видите пропорции головы в профиль Леонардо да Винчи

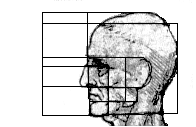
Пропорции головы в профиль. Леонардо да Винчи, 1488 г.

Слайд № 16

Те же пропорции мы можем с вам увидеть в следующих произведениях:

Леонардо до Винчи «Мадонна в гроте» (1483-1486)

Гутмес «Нефертити»

Слайд № 17

Можно приводить бесконечное число примеров. Так как искусству присущи стремление к стройности, соразмерности, гармонии.

8 .Гипотеза об истоке золотого сечения.

Пентаграмма – пятиконечная звезда

Слайд №18

В истории математики тесно связаны золотое сечение и правильные пятиугольники.

Последний в житейской практике называют пятиконечной звездой, а в науке — пентаграммой.

В III в. до н. э. Евклид рассматривал пропорцию, которую мы ныне называем золотым сечением, во II книге своих «Начал», а в следующих книгах использовал эту Пропорцию для построения правильного пятиугольника, десятиугольника, а также таких многогранников, как додекаэдр и икосаэдр.

И. Кеплер (1571-1630) в произведении «О шестиугольных снежинках» писал: «Построение пятиугольника невозможно без той пропорции, которую современные математики называют божественной»

Во времена Кеплера эпитетами «божественная», «чудесная», «превосходнейшая» награждали именно золотое сечение.

Попробуем построить пентаграмму – пятиконечную звезду.

Слайд № 18

Практическая работа № 5

1. Начертим окружность, разделим ее на пять равных

частей

2. Соединим последовательно точки деления,

3. Получим пятиугольник АВСОЕ с равными сторонами

и углами.

4. Проведем в нем диагонали.

5. А теперь обнаруживаем, что получили пятиконечную звезду.

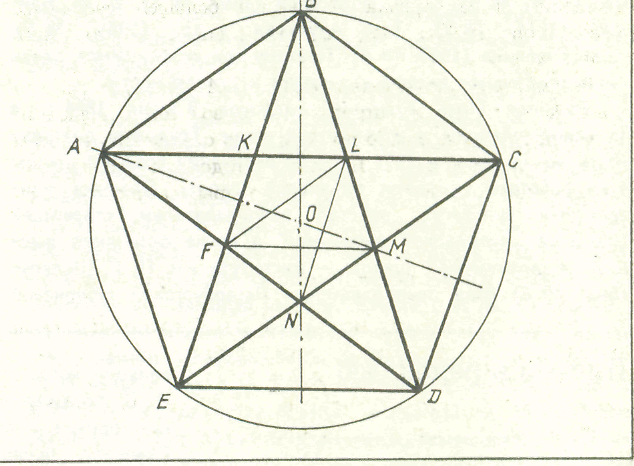
Теперь заметим, что если из вершины каждого из равнобедренных треугольников ДАС, ЕВД, АСЕ, БДА, СЕВ провести биссектрису (медиану, высоту), то все они пересекаются в одной точке О — центре описанной окружности.

Рассмотрим отрезки АК,КЛ,АЛ.

По рисунку видим , что точка К делит отрезок АЛ в золотом отношении, т.е

АЛ : АК = АК : КЛ = 1,6….

Получили , что эти отрезки связаны золотым отношением.

Все отрезки на сторонах пентаграммы составлены по закону золотого сечения, причем оно на каждой стороне присутствует двоекратно.

Слайд № 20

9. МУЗЫКА

А можно ли говорить о золотом сечении в музыке? Можно, если измерять музыкальное произведение по времени его исполнения. Золотое сечение в музыке отражает особенности восприятия временных пропорций. Точка золотого сечения приходится на кульминацию произведения.

Т. е. продолжительность звучания всего произведения относится к звучанию до кульминации как 1 к 1,618.

Пример

Время звучания – 4,06

Время до кульминации – 2,51

Золотое сечение 4,06 : 2,51 =1,61

А теперь попробуйте ответить мне на вопрос: почему классическая музыка – вечна, а современные хиты – музыка на час?

«Карие глаза»

К сожалению из-за недостатка времени мы не успеваем с вами рассмотреть золотое сечение в других произведениях искусства. Но мы убедились, что нет ни искусства без упражнений, ни упражнений без искусства.

Природа совершенна и у нее есть свои законы, выраженные с помощью математики и проявляющееся во всех искусствах.

И все же я хочу, чтобы сегодня на уроке вы проверили, сохраняется ли золотое сечение в работах великих художников.

Слайд №21

Практическая работа №6

У вас на столах распечатки репродукций. Рассчитайте пропорции и убедитесь сохранена ли форма золотого сечения.

10. Домашнее задание.

11.Подведение итогов урока

Выставление оценок учащимся

Литература:

Учебник по геометрии для 10-11 класса. М.: Мнемозина,2007
Васильченко К.В. «Путешествие в страну «Я». –Д.: Сталкер, 1998. – 448с.
Виленкин Н.Я., Чесноков А.С., Шварцбурд С.И.Математика: учебник для 5 класса.- М.: Мнемозина,2007.-280с.
Леман И.Увлекательная математика. Пер.с нем.– М.: Знание, 1985.-272с.
Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка: Пособие для учащихся. –М.: Просвещение, 1984. -160с.
Шуба М.Ю. Занимательные задания в обучении математике: Книга для учителя. – М.:Просвещение,1994.-222с.