Педагогический проект «Текстовые задачи школьного курса математики (базовый уровень), направленных на формирование специальных математических учебных действий и соответствующих им УУД при подготовке учеников к ГИА, ЕГЭ»

Министерство образования и науки Самарской области

Государственное автономное образовательное учреждение дополнительного профессионального образования (повышения квалификации) специалистов

САМАРСКИЙ ОБЛАСТНОЙ ИНСТИТУТ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ

И ПЕРЕПОДГОТОВКИ РАБОТНИКОВ ОБРАЗОВАНИЯ

ПЕДАГОГИЧЕСКИЙ ПРОЕКТ

«Построение многоуровневой системы задач по теме: Текстовые задачи школьного курса математики (базовый уровень), направленных на формирование специальных математических учебных действий и соответствующих им УУД при подготовке учеников к ГИА, ЕГЭ».

Автор проекта:

1.Шадыева Гулшевер Абляевна

2014.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

1.ФИО – Шадыева Гулшевер Абляевна,

2.Место работы- ГБОУ СОШ с. Троицкое Сызранского района Самарской области

3.Должность- учителя математики

4. Предмет- МАТЕМАТИКА

5. Класс 5-11

Введение

Решение задач является наиболее характерной и специфической   разновидностью свободного мышления.

Уильям Джеймс

В формировании многих качеств, необходимых успешному современному человеку, может большую роль сыграть школьная дисциплина — математика. Математика начинается не со счета, как всем думается, а с… загадки, проблемы. И эта загадка часто представляет собой текстовую задачу, то есть математическую задачу, в которой входная информация содержит не только математические данные, но еще и некоторый сюжет. Решая задачи, учащиеся приобретают новые математические знания , готовятся к практической деятельности. Вопреки тому, что решению математических задач в школьной программе уделяется недостаточное внимание, именно этот навык является одним из ключевых в жизни каждого человека. Принципы решения математических задач лежат в основе большинства точных дисциплин: химии, физики, информатики и т. д. Таким образом, не освоив эти принципы и не научившись их применять, ученик начинает испытывать серьезные трудности в изучении не только математики, но и других предметов.

Кроме того, в экзаменационную работу по математике за курс основной школы включен ряд заданий, требующих от обучающихся навыков решения текстовых задач. А значит, как перед учителем, так и перед учениками стоит задача — быть подготовленными к их решению. Учитель должен создать условия для формирования навыков решения текстовых задач, а ученик — приложить максимум умственных усилий для овладения методами решения таких задач. Огромная ценность текстовых задач состоит в том, что они являются материалом для ознакомления учащихся с новыми понятиями, для развития логического мышления. Этапы решения задач являются формами развития мыслительной деятельности.

Цель работы:

Систематизация текстовых задач школьного курса математики ;

• выделение базовых задач по данной теме;

• разделение задач на 2 уровня – базовый и углублённый, и 3 подуровня – знакомая задача, модифицированная задача и незнакомая задача (составление матрицы МСЗ)

Задачи:

— обучающие: анализировать и осмысливать текст задачи, самостоятельное выделение и формулирование познавательной цели, строить логическую цепочку рассуждений, критически оценивать полученный ответ, выбор наиболее эффективного способа решения задач, постановка и формулирование проблемы, выдвижение гипотез и их обоснование, смысловое чтение;

1. -развивающие: целеполагание, планирование своей деятельности в зависимости от конкретных условий, рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности, развитие творческой и мыслительной деятельности учащихся;

-воспитательные: смыслообразование, умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, воспитывать ответственность и аккуратность.

Основные цели решения текстовых задач в школьном курсе математики:

• научить переводить реальные предметные ситуации в различные математические модели,

• обеспечить действенное усвоение учащимися основных методов и приемов решения учебных математических задач.

Решение задач — практическое искусство. Научиться ему можно лишь подражая лучшим образцам и постоянно практикуясь. В ходе подобной практики могут выработаться и свои подходы к решению задач. Но надо помнить, что научиться решать задачи можно только решая их!

Многоуровневая система задач

Методика использования многоуровневой системы задач — это проектирование процесса обучения, основанного на построенной системе задач, организация контрольно-оценочной деятельности. В основе методики обучения на базе разработанной многоуровневой системы задач лежит поэтапное освоение блоков ее матрицы. Основная особенность этой методики заключается в том, что на каждом уровне, т.е. при освоении соответствующего столбца матрицы, ученик всякий раз сталкивается со всеми тремя видами учебных ситуаций, возникающих при решении задач. Благодаря этому осуществляется движение в предметно-содержательном и процессуально-деятельностном направлениях. Ведущим элементом методики является работа с ключевыми задачами. Эта работа выстраивается на постепенном переходе от совместных форм деятельности к индивидуальным. Введение новых понятий и теоретических фактов предваряется созданием проблемных учебных ситуаций, которые адекватно отражают и раскрывают содержание формируемого понятия (теоремы). Это позволяет представить новый теоретический материал в виде задачи или серии ключевых задач, которые нужно решить, для того чтобы справиться с проблемной ситуацией.

Составной частью используемой методики является постоянная систематизация изученного материала и соответствующая его визуализация в виде различных таблиц, схем, графов ключевых задач, которые вывешиваются для общего обозрения в кабинете и фиксируются учениками в своих тетрадях. Такая деятельность способствует формированию системности знаний.

Важным элементом методики служит составление на первом и втором уровнях задач самими учениками , а также задач на предметную и личностную рефлексию и самокоррекцию .Эта деятельность способствует осознанному усвоению полученных знаний, формированию прочных умений и навыков. Формирование многоуровневой системы задач темы можно осуществить с помощью ее матричного представления, выделяя ранжированный перечень базовых элементов содержания образования и соответствующие им ключевые задачи, – с одной стороны, и уровни обученности, отражающие умения решать знакомые, модифицированные и незнакомые задачи, – с другой. При составлении перечня элементов содержания образования отправной точкой служит кодификатор – список вопросов содержания школьного курса математики, усвоение которых проверяется при сдаче ЕГЭ.

При проектировании системы задач курса необходимо:

а) визуализировать наличие разных способов решения одной и одной и той же задачи,

б) дать формальное описание сложности того или иного решения задачи,

в) выделить ключевые задачи темы,

г) ранжировать ключевые задачи по уровням,

д) выделить равносильные задачи,

е) оценить масштабы тематической системы,

ж) сравнивать системы задач по теме в разных УМК.

Основные этапы технологии проектирования и применения многоуровневых систем задач следующие:

1) выделение уровней внешней дифференциации ( базовый и углубленный);

2) выделение подуровней внутренней дифференциации, определяемых готовностью учащегося действовать в знакомой заданной ситуации по готовому образцу; готовностью действовать в слегка видоизмененной или модифицированной ситуации ; готовностью находить решения в новой незнакомой ситуации, создавать алгоритм решения незнакомой задачи;

3) составление перечня базовых задач раздела программы;

4) конструирование матричной модели многоуровневой системы задач для каждой темы курса;

5) проведение занятий , уроков на основе многоуровневых систем задач, ведение мониторинга успешности математической деятельности, прогнозирование на его основе результатов ГИА и ЕГЭ.

Матричную модель удобно представить с помощью таблицы 1.

Матричная модель системы задач . Таблица 1

Предметно-содержательные уровни (определяются уровнем ключевых задач)
I	II	…	N
Уровни сформированности умения действовать в ситуации	I (знакомая)
	II (модифицированная)
	III (незнакомая)

Такая матрица системы задач темы содержит 3 строки, соответствующие трем типам учебных ситуаций, возникающих при решении задач, и N столбцов, отражающих количество уровней в выделенной системе ключевых задач темы. Совокупность ключевых задач некоторого уровня естественно назвать базисом пространства задач этого уровня, так как они используются при решении задач данной темы, а в написанном решении учебной задачи мы обнаружим ту или иную комбинацию ключевых задач.

Подобное табличное (матричное) представление системы задач темы помогает осуществить полноценное наполнение на каждом уровне ее предметного и дидактического компонентов и тем самым реализовать критерии предметной и дидактической полноты (относительно заданных целей) формируемой системы учебных задач. При этом если ключевые задачи выполняют в системе роль своеобразных интеграторов предметно-содержательной компоненты, то при проектировании и реализации процесса обучения аналогичную роль должны играть общие методы и приемы деятельности в выделенных ситуациях.

Благодаря матричной структуре, обеспечивающей движение в предметно-содержательном и процессуально-деятельностном направлениях, описываемую систему задач легко приспособить к конкретному ученику. Именно матричная структура многоуровневой системы задач (МСЗ) является основой для проявления гибкости, обеспечивающей построение индивидуальных траекторий обучения.

Другим основополагающим элементом является работа с ключевыми задачами. Эта работа выстраивается на постепенном переходе от совместных форм деятельности к индивидуальным. На начальных этапах изучения курса предпочтение отдается фронтальному разбору отдельных ключевых задач. На следующей стадии разбор отдельных задач сменяют уроки решения ключевых задач темы. На заключительных этапах изучения темы ученики выполняют групповые и индивидуальные проекты по самостоятельному решению и составлению целесообразной последовательности ключевых задач .

При построении системы задач могут применяться различные системообразующие основания и критерии. Однако каждая система учебных задач должна характеризоваться следующими основными инвариантными признаками:

а) целостность, т.е. наличие явных и латентных горизонтальных и вертикальных интегрирующих предметно-содержательных и дидактических связей;

б) дидактическая полнота (функциональная достаточность), позволяющая реализовать стимулирующую, обучающую, развивающую, воспитывающую, контролирующую, оценочную, прогностическую и коммуникационную функции учебных задач;

в) предметно-содержательная полнота относительно требований к нормативным уровням обученности по завершению учебного курса, выраженная в наличии задач разных уровней сложности и трудности.

• Задачи, решаемые по образцу, предполагающие только воспроизведение алгоритма, условно называем знакомыми задачами (ЗЗ).

• Задачи, в которых требуется сделать хотя бы один самостоятельный шаг : преодолеть техническую сложность, видоизменить какое– либо звено алгоритма, условно назовём модифицированной задачей ( МЗ).

• Задачи, аналогов которых учитель не демонстрировал, готовых алгоритмов нет, которые при первом прочтении трудно отнести к какому– либо изученному типу, можно назвать незнакомыми задачами (НЗ).

Формируемые УУД в рамках ФГОС при решении текстовых задач. Таблица№2.

№

Этапы решения задач	Формируемые УУД
	Анализ условия (введение буквенных обозначений)	целеполагание; выделение существенной информации; формулирование задачи и прогнозирование способов решения; аналогия; классификация; знакосимволические действия.
	Схематическая запись условия задачи в виде таблицы, схемы, графа с введенными буквенными обозначениями	планирование; систематизация; знакосимволические действия; моделирование.
	Составление модели (поиск аналога, привлечение из математики или физики известного закона)	создание способа решения задачи; корректировка условия; моделирование в графическом виде.
	Решение уравнения, системы и т.д. (поиск неизвестного)	анализ и выявление существенной информации; выведение следствий; построение цепи рассуждений; выдвижение и проверка гипотез; преобразование модели.
	Интерпретация модели (проверка и оценка решений, корней)	анализ; выведение следствий; конкретизация; знакосимволическое действие (интерпретация).
	Исследование (обобщение задачи или способа её решения для видоизмененных условий, другие подходы к решению)	анализ; синтез; поиск аналогов; построение цепи рассуждений; умение сжато передать содержание; умение применять схемы, символы, модели; создание способов решения проблем поискового, творческого характера.
	Рефлексия	смыслообразование; планирование; контроль; коррекция; оценка; волевая саморегуляция; готовность к саморазвитию, к самообразованию; умение ставить и формулировать для себя новые задачи; развивать мотивы и интересы своей образовательной деятельности.

Перечень базовых задач по теме: «Текстовые задачи»

Б З 1: Задача вычисления отношения величин.( пропорции; прямо пропорциональные и обратно пропорциональные величины)

Б З 2: Вычисление дроби от числа, процента от числа, процента от числа.

Б З 3: Вычисление числа по его дроби, по его процентам.

Б З 4: Вычисление отношения ,процентного отношения двух чисел.

Б З 5: Деление числа в данном отношении.

Б З 6: Применение прямой и обратной пропорциональности величин к решению различных задач.

Б З 6.1: Задачи на проценты, меси, сплавы, концентрацию, разбавление.

Б З 6.2: Задачи на равномерное движение.

Б З 6.3: Задачи на работу.

Б З 6.4: Задачи на запись чисел.

МСЗ( многоуровневая система задач)

по теме : Текстовые задачи школьного курса математики. Таблица №3.

Уровни внеш. дифф.

Подуровни внутр. дифф.	БЗ 1. Задача вычисления отношения величин.	БЗ 2. Вычисление дроби от числа, процента от числа, процента от числа.	БЗ 3. Вычисление числа по его дроби, по его процентам.	БЗ 4. Вычисление отношения, процентного отношения двух чисел.	БЗ 5. Деление числа в данном отношении.	БЗ 6. Применение прямой и обратной пропорциональности величин к решению различных задач практического содержания.
						БЗ 6. 1. Задачи на проценты, меси, сплавы, концентрацию, разбавление.	БЗ 6.2. Задачи на равномерное движение.	БЗ 6.3 Задачи на работу.	БЗ6.4 Задачи на запись чисел.
Общеобразовательный уровень (ОУ)	ЗЗ	Узнавание пропорциональных величин, нахождение их в данной совокупности	Простейшие задачи в одно действие по арифметике, геометрии, биологии… линейные уравнения	Простейшие задачи в одно действие по арифметике, геометрии, биологии… линейные уравнения, обратные к БЗ 2	Простейшие задачи в одно действие по вычислению отношения, процентного отношения двух чисел.	Задачи, обратные к БЗ 4 Простейшие задачи в одно действие по вычислению отношения, процентного отношения двух чисел	Математическая модель задачи сразу, без промежуточных операций, сводится к составлению, а затем решению линейного, дробно-рационального, квадратного уравнения с одной неизвестной или системе линейных уравнений с двумя неизвестными.
	МЗ	Нахождение закономерности, формулы, аналитической зависимости	Задачи сложного процентного роста ( убывания с постоянной процентной ставкой; нахождение % от чисел или выражений с учетом дополнительных данных. Системы линейных уравнений)	Задачи сложного процентного роста ( убывания с постоянной процентной ставкой; нахождение % от чисел или выражений с учетом дополнительных данных. Системы линейных уравнений), обратные к БЗ 2	Задачи, требующие несколько промежуточных операций, приводящие к линейному уравнению или системе линейных уравнений.	Задачи, обратные к БЗ 4 Задачи, требующие несколько промежуточных операций, приводящие к линейному уравнению или системе линейных уравнений	Математическая модель задачи в результате нескольких промежуточных операций, сводится к составлению, а затем решению линейного, дробно-рационального, квадратного уравнения или неравенства с одной неизвестной или системе линейных, дробно-рациональныхквадратных уравнений или неравенств с двумя неизвестными. Исследование полученных моделей
	НЗ	Выявление пропорциональных величин в окружающей действительности	Задачи сложного процентного роста ( убывания) с переменной процентной ставкой; нахождения % от чисел или выражений с учетом скрытых связей; нелинейные уравнения и их системы	Задачи сложного процентного роста ( убывания) с переменной процентной ставкой; нахождения % от чисел или выражений с учетом скрытых связей; нелинейные уравнения и их системы, обратные к БЗ 2	Задачи, требующие несколько промежуточных операций, установление связей между величинами, приводящие к линейному , дробно-рациональному, квадратному уравнению или системе уравнений	Задачи, обратные к БЗ 4 Задачи, требующие несколько промежуточных операций, установление связей между величинами, приводящие к линейному , дробно-рациональному, квадратному уравнению или системе уравнений	Математическая модель задачи сводится к составлению, а затем решению уравнений, неравенств или систем с функциями указанных типов, содержащие элемент технического усложнения, модуль, параметр, целочисленные неизвестные.
Углубленный уровень (УУ)	ЗЗ	Узнавание пропорциональных величин, нахождение их в данной совокупности в расширенной предметной области: за счет включения теории чисел и тд.	Задачи математическая модель которых состоит из 3 и более линейных уравнений , неравенств и соотношений относительно неизвестных величин задачи.	Задачи математическая модель которых состоит из 3 и более линейных уравнений , неравенств и соотношений относительно неизвестных величин задачи обратные к БЗ 2	Задачи, требующие несколько промежуточных операций, содержащие элемент технического усложнения приводящие к линейному , дробно-рациональному, квадратному уравнению или системе уравнений	Задачи, обратные к БЗ 4 Задачи, требующие несколько промежуточных операций, содержащие элемент технического усложнения приводящие к линейному , дробно-рациональному, квадратному уравнению или системе уравнений	Математическая модель задачи сводится к составлению, а затем решению системы двух или трех уравнений с двумя или тремя неизвестными. Модель может включать комбинированные системы, содержать буквенные выражения и параметры.
	МЗ	Нахождение закономерности, формулы, аналитической зависимости в расширенной предметной области: за счет включения теории чисел и тд.	Задачи математическая модель которых состоит из уравнений и, неравенств относительно неизвестных величин задачи. (нелинейных)	Задачи математическая модель которых состоит из уравнений и, неравенств относительно неизвестных величин задачи. (нелинейных)	Задачи, требующие несколько промежуточных операций, установлению скрытых связей, содержащие элемент технического усложнения приводящие к линейному , дробно-рациональному, квадратному уравнению или системе уравнений	Задачи, обратные к БЗ 4 Задачи, требующие несколько промежуточных операций, установлению скрытых связей, содержащие элемент технического усложнения приводящие к линейному , дробно-рациональному, квадратному уравнению или системе уравнений	Задачи на ситуации содержит неявные, скрытые связи. Математическая модель может сводиться к неопределённой системе, может содержать технически сложно-решаемые уравнения или системы (уравнений и неравенств, требующих перебор вариантов решений и ответов)
	НЗ	Выявление пропорциональных величин в окружающей действительности в расширенной предметной области: за счет включения теории чисел и тд.	Задачи математическая модель которых состоит из уравнений с целочисленными неизвестными, количество уравнений меньше числа неизвестных.	Задачи математическая модель которых состоит из уравнений с целочисленными неизвестными, количество уравнений меньше числа неизвестных обратные к БЗ 2.	Задачи, требующие несколько промежуточных операций, установлению скрытых связей, содержащие элемент технического усложнения приводящие к линейному , дробно-рациональному, квадратному уравнению или системе уравнений. Анализ и интерпретация полученного решения.	Задачи, обратные к БЗ 4 Задачи, требующие несколько промежуточных операций, установлению скрытых связей, содержащие элемент технического усложнения приводящие к линейному , дробно-рациональному, квадратному уравнению или системе уравнений. Анализ и интерпретация решения.	Математическая модель может содержать неопределенную систему; приводить к функциональному уравнению или рекуррентному соотношению, провоцировать ошибку из-за ложных стереотипов

Задачи общеобразовательного уровня (ОУ)

БЗ 1. Задача вычисления отношения величин.

• Знакомые задачи (ЗЗ)

1. Из 20 кг яблок получается 16 кг яблочного пюре. Сколько яблочного пюре получится из 45 кг яблок?

2. За 8 часов рабочий изготавливает 96 одинаковых деталей. Сколько деталей изготовит рабочий за 15 часов?

3. В саду росло 17 деревьев, 12 из них яблони, а остальные груши. Какую часть всех деревьев составляют грушевые деревья?

4. Сырок стоит 7 рублей 20 копеек. Какое наибольшее число сырков можно купить на 60 рублей?

5. Теплоход рассчитан на 1000 пассажиров и 30 членов команды. Каждая спасательная шлюпка может вместить 50 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды?

6. В пачке 250 листов бумаги формата А4. За неделю в офисе расходуется 700 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 8 недель?

7. Аня купила месячный проездной билет на автобус. За месяц она сделала 41 поездку. Сколько рублей она сэкономила, если проездной билет стоит 580 рублей, а разовая поездка 20 рублей?

• Модифицированные задачи (МЗ)

1. Длина детали на чертеже, сделанном в масштабе 1 : 5, равна 7,2 см. Чему будет равна длина этой детали на другом чертеже, сделанном в масштабе 1 : 3 ? в масштабе 2 : 1 ?

2. Зоя купила в магазине 18 яблок. Эти яблоки разделили между мамой, папой и Зоей в отношении 2:1:3, то есть мама получила 2 части, папа 1 часть, а Зоя 3 части всех яблок. Сколько яблок получил каждый?

3. Две бригады школьников, работая с одинаковой производительностью, пропололи морковь на участке, площадь которого составляет 15 соток. Причем одна бригада работала 2 часа, а другая 3 часа. Сколько соток прополола каждая бригада?

4. Для приготовления маринада для огурцов на 1 литр воды требуется 14 г лимонной кислоты. Лимонная кислота продается в пакетиках по 10 г. Какое наименьшее число пачек нужно купить хозяйке для приготовления 6 литров маринада?

5. Шоколадка стоит 30 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок можно получить на 500 рублей в воскресенье?

• Незнакомые задачи (НЗ)

1. Числитель дроби на 1 меньше знаменателя. Если эту дробь сложить с обратной ей дробью, то получится 2 1/12. Найдите исходную дробь.

2. Две бригады школьников получили за сбор клубники 2725 рублей. Причем в одной бригаде было 11 человек, а в другой 9 человек. Первая бригада работала, а вторая 6 дней. Как распределить между бригадами полученную сумму, если все школьники работали в одинаковых условиях?

3. Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 8 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?

4. Таксист за месяц проехал 6000 км. Стоимость 1 л бензина (в городе) 20 рублей Средний расход бензина на 100 км составляет 9 л. Сколько рублей потратил таксист на бензин за этот месяц?

5. Аня купила месячный проездной билет на автобус. За месяц она сделала 41 поездку. Сколько рублей она сэкономила, если проездной билет стоит 580 рублей, а разовая поездка 20 рублей?

6.Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?

РЕШЕНИЕ

Серьезная задача, связанная со здоровьем, поэтому будем предельно внимательны.

а). Подсчитаем в граммах сколько же надо больному лекарства по данным задачи по 0,5 г 3 раза в день в течение 21 дня. Для этого достаточно все данные перемножить 0,5*3*21=0,5*63=31,5 (грамма)

б). Теперь раз в задаче спрашивают количества упаковок. Определим сколько граммов лекарства содержится в 1 упаковке, для этого общее количество таблеток лекарства в упаковке умножим на их массу 10*0,5=5 (грамм)

в). И наконец, подсчитаем сколько же нам надо упаковок. Разделим общее количество массы лекарства из пункта 1 на массу лекарства в одной упаковке, пункт 2:

31,5:5=6,3 (упаковки)

г). Остается записать ответ, но прежде проанализируем полученное 6 целых и 0,3 упаковки. Именно столько строго математически нужно больному на курс лечения. Но поскольку 0,3 упаковки на не продадут, а больной без лекарства не поправится, мы должны купить 7 целых упаковок, хоть и останется лишнее лекарство.

ОТВЕТ: 7

Б З 2: Вычисление дроби от числа, процента от числа.

• Знакомые задачи (ЗЗ)

1.По норме рабочий должен изготовить 45 деталей. Он выполнил норму на 120%. Сколько деталей изготовил рабочий?

2. Сбербанк выплачивает вкладчикам 24% годовых. Сколько выплатил сбербанк дополнительно к вкладу, если вклад составил 3000 рублей?

3. В классе 36 учеников. В спортивных секциях занимается 75% всех учащихся класса. Сколько в классе учеников не занимаются в спортивных секциях?

4. Цена книги понизилась на 15%. Найдите новую цену книги, если прежняя составляла 60 рублей?

5. Средняя продолжительность жизни у мужчин считается 75 лет. У алкоголиков она снижается на 20%. Какова средняя продолжительность их жизни?

6.В свежих яблоках 80% воды, а в сушеных — 20%. На сколько процентов уменьшается масса яблок при сушке?

Решение:

Свежие   х (кг)   100 – 80 = 20(%) = 0,2     0,2х (кг)

Сушен.   у (кг)    100 – 20 = 80(%) = 0,8     0,8у (кг)

Уравнение:     0,2х = 0,8у

у : х =0 ,2 : 0,8

у : х = 0,25

у : х = 25 : 100

у = 25%;  х = 100%

100 – 25 = 75(%)

                                                           Ответ:   на 75%     

• Модифицированные задачи (МЗ)

1. В первую неделю бригадой было выполнено 30 % месячной нормы, во вторую неделю – 0,8 того что было выполнено в первую неделю, а в третью неделю – 2/3 того, что выполнили во вторую неделю. Сколько процентов месячной нормы осталось выполнить бригаде в четвертую неделю?

2. В начале года число мужчин, работавших на заводе, составляло 40% от общей численности работников завода. После того, как были приняты на работу еще 6 мужчин, а 5 женщин уволилось, число мужчин и женщин на заводе сравнялось.
Сколько человек работало на заводе в начале года?

3. Возраст брата составляет 40% от возраста сестры.
Сколько процентов составляет возраст сестры от возраста брата?

4. Влажность купленного арбуза составила 99%. В результате длительного хранения влажность снизилась до 98%.
Как изменилась масса арбуза?

5. Двое путников одновременно вышли из пункта А по направлению к пункту В.
Шаг второго был на 20 % короче, чем шаг первого, но зато второй успевал за то же время сделать на 20% шагов больше, чем первый. Сколько времени потребовалось второму путнику для достижения цели,
если первый прибыл в пункт В спустя 5 часов после выхода из пункта А ?

6. Цену товара сначала снизили на 30%, а затем новую цену снизили на 10%. На сколько процентов всего снизили первоначальную цену товара? В первой упаковке из 150 книг 32% составляют учебники по алгебре, а во второй упаковке из 210 книг 20% учебники по алгебре. Какой процент всех книг составляют учебники по алгебре?

Решение: 150*0.32=48 книг в первой упаковке(алгебра)

во второй 210*0.2=42 книг по алгебре

всего их 48+42=90 книг по алгебре

всего книг 150+210=360 книг
Чтобы найти процентное содержание книг по алгебре во всех книгах надо количество книг по алгебре разделить на общее количество книг

значит 90/360=0.25 или 25%

1) 150 х 32 : 100 = 48 учебников по алгебре в 1 упаковке

2) 210 х 20 : 100 =42  учебника по алгебре во 2 упаковке

3) 48 + 42 = 90 учебников пр алгебре всего

4) 150 +210 = 360 книг в двух упаковках

5) 90 х 100 % : 360 =25 % от всех книг составляют учебники по алгебре

• Незнакомые задачи (НЗ)

1.На 1ой базе находится в 2 раза больше подшипников, чем на 2ой. К концу месяца с 1ой базы было поставлено в торговую сеть 80% подшипников, а со второй – 40%. На какой базе осталось больше подшипников? Ответ: на второй базе.

2. В начале года число мужчин, работавших на заводе, составляло 40% от общей численности работников завода. После того, как были приняты на работу еще 6 мужчин, а 5 женщин уволилось, число мужчин и женщин на заводе сравнялось.
Сколько человек работало на заводе в начале года?

3. Для нормальной работы пансионата требуется 600 лампочек. Каждый месяц требуется замены 10% лампочек. Сколько необходимо лампочек для нормальной работы пансионата?

4. В городе N живет 250000 жителей. Среди них 15 % детей и подростков. Среди взрослых 35% не работает (пенсионеры, студенты, домохозяйки и т.п.). Сколько взрослых работает?

5. Плоды ананаса содержат 84% воды. Остальное питательные вещества и сахар. Сахар составляет 25% массы остатка. Сколько сахара содержится в 175 кг плодов ананаса?

6. За килограмм одного продукта и 10 кг другого заплачено 200 рублей. Если при сезонном изменении цен первый продукт подорожает на 15%, а второй подешевеет на 25%, то за такое же количество этих продуктов будет заплачено 182 рубля. Сколько стоит килограмм каждого продукта?

РЕШЕНИЕ:

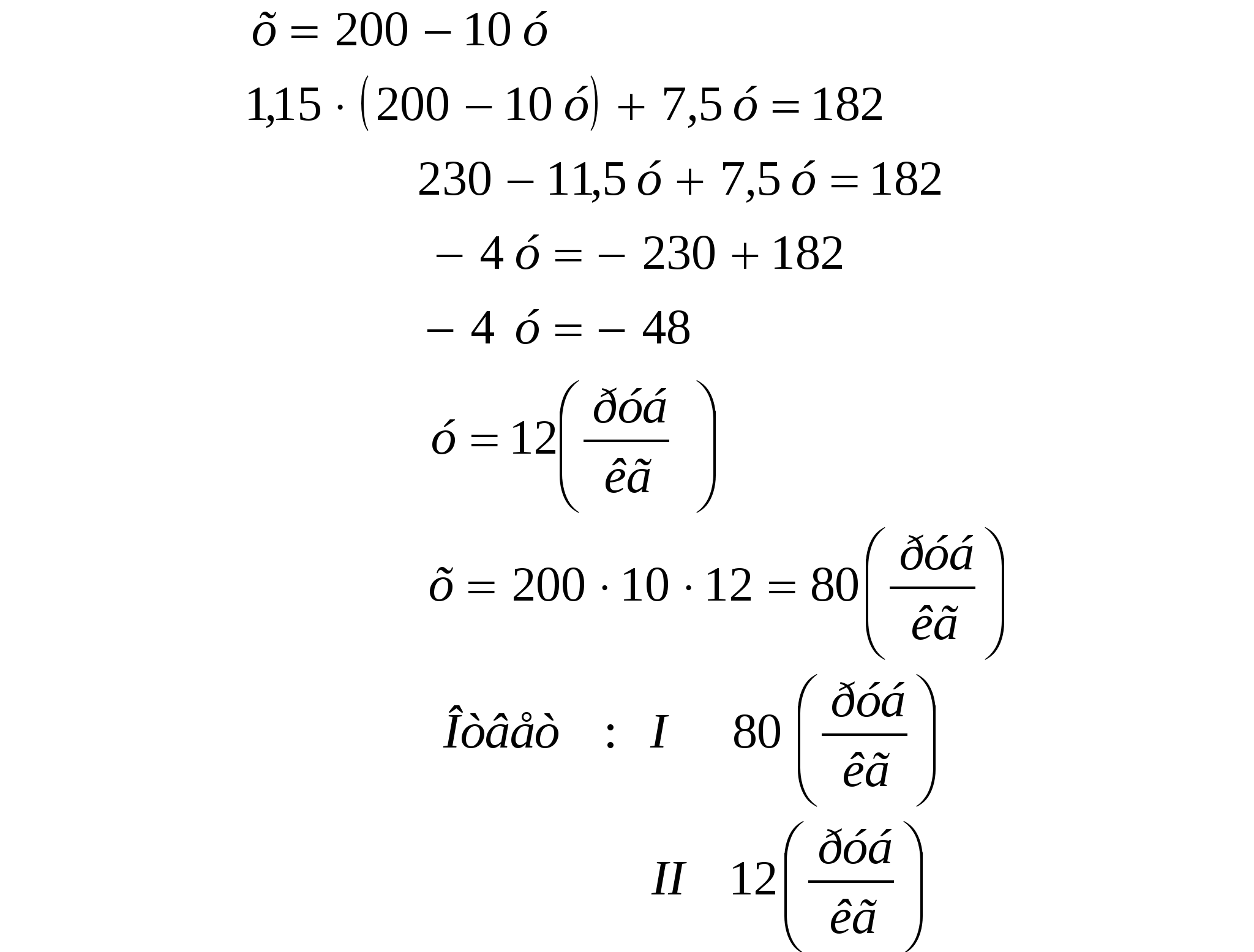
Б З 3: Вычисление числа по его дроби, по его процентам.

• Знакомые задачи (ЗЗ)

1 Призерами городской олимпиады по математике стало 48 учеников, что составило 12% от числа участников. Сколько человек учувствовало в олимпиаде?

2. Папа вложил 5000 р. В акции своего предприятия и получил 20% дохода. Сколько рублей дохода получил папа?

3. Цена на электрический чайник была повышена на 22% и составила 1830 рублей. Сколько рублей стоил чайник до повышения цены?

4. Расчистили от снега катка, что составляет 800 м². Найдите площадь всего катка.

5. Девочка прошла на лыжах 300 м, что составляло  всей дистанции. Какова длина дистанции?

6.     При покупке в кредит цветного телевизора было уплачено наличными 234 р., что составляет 36% стоимости телевизора. Сколько стоит телевизор?

7. В школе на родительском собрании отсутствовало 12 человек, что составляет 7,5% от общего числа родителей. Сколько всего родителей должно было присутствовать на собрании?

8. Завод должен был изготовить по месячному плану некоторое число моторов. За месяц он выполнил план на 116% и дал 1 740 моторов. Каков был месячный план?

9.За месяц до экзаменов 75% выпускников уже определились, какие экзамены по выбору они будут сдавать. При этом 60% из них решили сдавать геометрию. Сколько процентов из не определившихся должны выбрать геометрию, чтобы по крайней мере половина учащихся сдавала этот экзамен?

РЕШЕНИЕ: Всего 100% х(уч)
Определились 75% 0,75х(уч)
Геометрия 60% 0,6.0,75х = 0,45х(уч)
Не определились 25% 0,25х(уч)
Из них геометрия у% 0,01у ∙ 0,25х = 0,0025ху(уч)
Уравнение: 0,45х + 0,0025ху = 0,5х
0,0025ху = 0,05х
у =
у = 0,20 = 20%
Ответ: 20%.

• Модифицированные задачи (МЗ)

1.Когда Костя прошел 0,3 всего пути от дома до школы, ему ещё осталось пройти до середины пути 150 км. Какой длины путь от дома Кости до школы?

2. Железнодорожный билет для взрослого стоит 780 рублей. Стоимость билета для школьника составляет 50% от стоимости билета для взрослого. Группа состоит из 19 школьников и 3 взрослых. Сколько рублей стоят билеты на всю группу?

3.  Автомобиль прошел в первый час всего пути, во второй час оставшегося пути, а в третий час остальной путь. Известно, что в третий час он прошел на 40 км меньше, чем во второй час. Сколько километров прошел автомобиль за эти 3 ч?

4. Три группы школьников посадили деревья вдоль дороги. Первая группа посадила 35% всех имевшихся деревьев, вторая — 60 % оставшихся деревьев, а третья группа — остальные 104 дерева. Сколько всего деревьев посадили?

5. Из полной бочки взяли 14,4 кг квашеной капусты и затем еще этого количества. После этого в бочке осталось находившейся там ранее квашеной капусты. Сколько килограммов квашеной капусты было в полной бочке?

6.Одна таблетка лекарства весит 35 мг и содержит 8% активного вещества. Ребёнку в возрасте до 6 месяцев врач прописывает 0,8 мг активного вещества на каждый килограмм веса в сутки. сколько таблеток этого лекарства следует дать ребёнку весом 7 кг в течение суток?

Решение: 35 мг — 100%

 х мг — 8%

х= 35*8/100 = 2,8 мг — активного в-ва содержится в 1-ой таблетке

2,8 : 0,8 = 3,5 таблеток в сутки следует дать ребенку

 8%=0,08

1) 35*0,8=2,8 (мг) вещества содержится в одной таблетке.

2) 0,8*7=5,6 (мг) вещества можно давать ребенку в течение суток.

3) 5,6:2,8=2 (таб.) Ответ: 2 таблетки этого лекарства следует давать ребенку весом 7 кг в течение суток.

• Незнакомые задачи (НЗ)

1 Три группы школьников посадили деревья вдоль дороги. Первая группа посадила 35% всех имеющихся деревьев, вторая – 60% оставшихся деревьев, а третья группа – остальные 104 дерева. Сколько деревьев посадили?

2.Одна таблетка лекарства весит 20 мг и содержит 5% активного вещества. Ребенку в возрасте до 6 месяцев врач прописывает 2 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребенку в возрасте четырех месяцев и весом 7 кг в течение суток?

3. Несколько лет назад сберегательный банк выплачивал доход по срочному вкладу из расчета 3% годовых от вложенной суммы. Сколько рублей оказывалось на счете через 2 года, если на него положили 10000 р.?

4. Банк выплачивает вкладчикам каждый год 8% от внесенной суммы. Клиент сделал вклад в размере 200000 рублей. Какая сумма будет на его счете через 5 лет?

5. Для токаря установлена норма выработки — 500 деталей в день, но он перевыполняет норму. В первый день он выполнил 105% нормы, во второй день — 107%, в третий день — 110%, в четвёртый день— 106% и в пятый день — 108%. Сколько деталей он изготовил в каждый из этих дней?

6. В библиотеке имеются книги на английском, французском и немецком языках. Английские книги составляют 36 % всех книг, французские — 75 % английских книг, а остальные 185 книг – немецкие. Сколько всего книг в библиотеке?

7. За килограмм одного продукта и 10 кг другого заплачено 20 рублей. Если при сезоном изменении цен первый продукт подорожал на 15 %, а второй подешевел на 25 % , то за тоже количество этих продуктов будет заплачено 18,2 рублей. Сколько стоит 1 кг каждого продукта? в огурцах 99 % воды. 8.Через некоторое время часть воды испарилась и ее стало 98%. На сколько процентов уменьшилась масса огурцов?

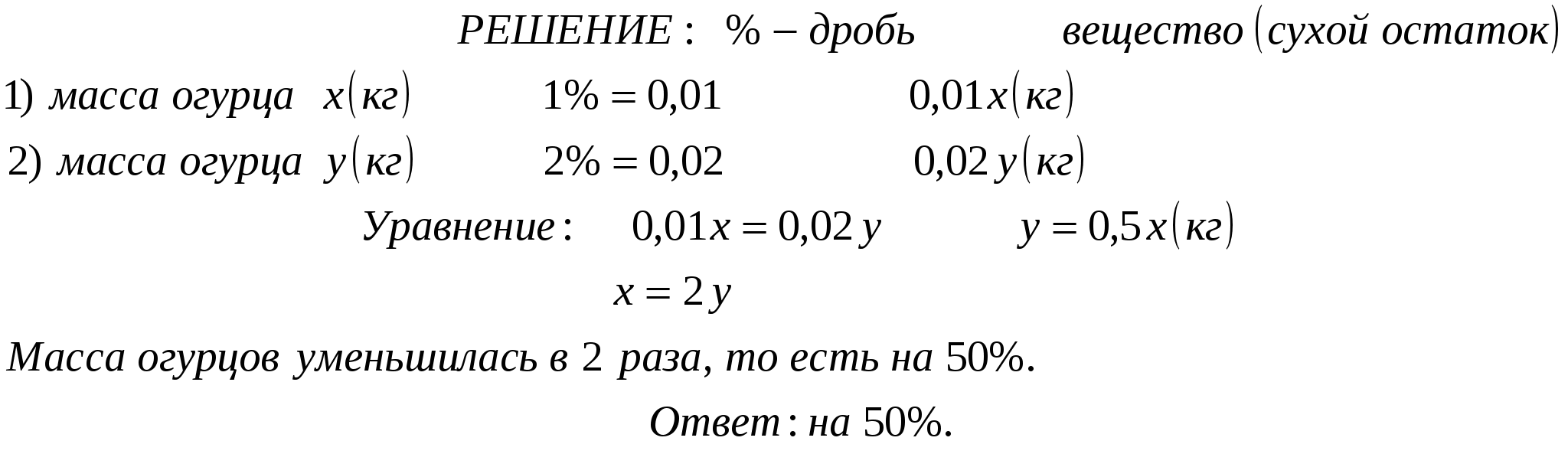
Б З 4: Вычисление отношения ,процентного отношения двух чисел.

• Знакомые задачи (ЗЗ)

1 Какую часть урока заняла самостоятельная работа, которая длилась 20 мин, если продолжительность урока 45 мин?

2. Завод должен был за месяц изготовить 1 200 изделий, а изготовил 2 300 изделий. На сколько процентов завод перевыполнил план?

3. Урожайность пшеницы в хозяйстве за предыдущий год составила 42 ц/га и была занесена в план следующего года. В следующем году урожайность снизилась до 39 ц/га. На сколько процентов был выполнен план следующего года?

4. Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена цена на футболку?

5. На собрании присутствовали 200 человек. За предложенную резолюцию голосовали 151 человек. Сколько процентов участников собрания голосовало за резолюцию?

6. По плану рабочий должен был изготовить 800 деталей, а изготовил 996 деталей. Сколько процентов плана он выполнил?

7. На 10 кг муки получилось 4,5 кг припёка. Сколько процентов  составляет  припёк от данного количества муки?

8. При плановом задании 60 автомобилей в день завод выпустил 66 автомобилей. На сколько процентов завод выполнил план?

• Модифицированные задачи (МЗ)

1 Мобильный телефон стоил 3500 рублей. Через некоторое время цену на эту модель снизили до 2800 рублей. На сколько процентов была снижена цена?

2. Мы пошли в магазин покупать мне зимние ботинки. Родители выделили на их покупку 2000 руб. В магазине мне понравились ботинки стоимостью 2300 руб. На них была скидка 25%. Мне стало любопытно, хватит ли у нас денег купить их?

3. В обед врачи рекомендуют употреблять 45% всей дневной пищи. А ужин должен составлять 1/3 обеда. Какой % дневной нормы составит ужин?

4. В магазине книга стоит 400 рублей, а на рынке 380 рублей. Найти какой процент составляет рыночная цена по отношению к магазинной?

5. Участок леса содержит 96% сосен. Лесозаготовительная компания планирует вырубить на этом участке 150 сосен, в результате чего их содержание понизится до 95%. Сколько сосен останется на участке? разделить 125 на такие 4 части, чтобы первая часть относилась ко второй , как 2:3 , вторая к третей , как 3:5, а третья к четвёртой, как 5:6

Решение: Пусть х  одна часть. Тогда первое число 2х, вторая 3х,третья 5х, четвертая 6х

2х+3х+5х+6х=125

16х=125

х=125/16 приходится на одну часть

125/16*2=125/8=15,625-одно число, 125/16*3=23,4375 (второе число),

125/16*5=39,0625— третье число, 125/16*6=46,875 четвертое число.

6. В городе имеется два молокозавода. Партию молока поступающего с близлежащих ферм первый завод может переработать за 6 часов, а второй за 9 часов. Сколько процентов молока из этой партии должно поступать на первый завод, чтобы вся партия перерабатывалась за меньшее время?

Решение:

1/6 : 1/9 = 1,5, т.е. скорость работы I завода в 1,5 раза больше II завода

Пусть x % поступило на II завод, тогда на I – 1,5 х

х + 1,5 х = 100

2,5х = 100

х = 40

40 · 1,5 = 60 %

Ответ: 60 %.

• Незнакомые задачи (НЗ)

1 Цена товара была дважды снижена на одно и то же число процентов. На сколько процентов снижалась цена товара каждый раз, если его первоначальная стоимость 2000р., а окончательная 1805 р.?

2. Для засолки огурцов был нужен 9% раствор уксусной кислоты, в наличии был 70% ра-р. Мама попросила меня посчитать сколько надо добавить воды в 20гр. 70% раствора, что бы получить 9% раствор.

3. Найти прибыль от 30000 рублей положенных на депозит на 3 года под 10% годовых, если в конце каждого года проценты добавлялись к депозитному вкладу.

4. В банк на депозит на 3 года положили 30000 рублей под 10% годовых. а) Найдите насколько прибыльнее был бы вариант, когда годовой доход добавлять к счету, на который в будут начисляться проценты, чем вариант, когда проценты каждый год забираются клиентом? б) Какая будет разница через 10 лет?

5. Влажность свежескошенной травы 70%, а влажность сена 16%. Сколько надо скосить травы, чтобы получить 1 т сена?

6. Перерабатывая цветочный нектар в мед, пчелы освобождают его от значительной части воды. Нектар содержит 70% воды, а мед 16%. Сколько килограммов нектара надо переработать для получения 1 кг меда?

7.Семья Ивановых ежемесячно платит за коммунальные услуги, телефон и электричество. Если бы коммунальные услуги подорожали на 50%, то общая сумма платежа увеличилась  бы на 35%. Если бы электричество подорожало на 50%, то общая сумма платежа увеличилась бы на 10%.  Какой процент от общей суммы платежа приходится на коммунальные услуги, телефон и электричество?

 

Решение:

 Комм. усл.  х%     150% = 1,5     1,5х

 Телефон    у%                                 у

Электр.       z%                                 z

             (x + у + z)%  135% = 1,35    1,35 (х + у + z)

 

                    х%                                 х

                    у%                                 у

                   z%        150%=1,5       1,5z

            (х + у + z)         110% = 1,1      1,1(х + у + z)

 

 Решаем систему уравнений:

 х + у + z = 100

1,5х + у + z = 1,35(х + у + z)

 х + у + 1,5z = 1,1(х + у + z)

 

 После элементарных преобразований уравнений находим

 х = 70% ;  у = 10%  ;   z = 20%   и это ответ на вопрос задачи.      

8.    В кувшин налили 3 литра молока 8 % жирности, некоторое количество молока 2 % жирности и тщательно перемешали. Определите, сколько литров молока 2 % жирности было налито в кувшин, если известно, что жирность молока, полученного после перемешивания, составила 6 %?

Решение: пусть х л молока – 2 % жирности

3 · 0,08 = 0,24 жира в 3 литрах 8 % молока

х · 0,02 – жира в х литрах 2 % молока

0,24 + 0,02х = 0,06(3+ х)

0,24 + 0,02х = 0,18 + 0,06х

х = 1,5 л

Ответ: 1,5 литра.

9. Клиент внес 3000 рублей на два вклада, один из которых даёт годовой доход равный 8 %, а другой – 10 %. Через год на двух счётах у него было 3260 рулей. Какую сумму клиент внес на каждый вклад?

Решение: пусть первый вклад – х руб., а второй – y рублей. Тогда через год (с доходом) первый: х + 0,08х, а второй: y + 0,1y

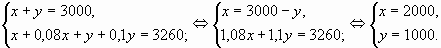
 Ответ: 2000 и 1000 рублей.

Б З 5: Деление числа в данном отношении.

• Знакомые задачи (ЗЗ)

1. Для приготовления повидла нужно взять яблоки и сливы в отношении 5:8. Сколько килограммов яблок и сколько килограммов слив ушло на повидло, если всего было 3 кг 250 г фруктов?

2. У Юли, Иры и Алины было 28 карандашей, Девочки поделили их в отношении 2:2:3. Известно, что больше всего карандашей досталось Алине. Сколько карандашей у Алины?

3. Для приготовления ягодного варенья берутся объемы ягод и сахара в отношении 1 : 1. Сколько литров сахара нужно досыпать к 5 литрам ягод, чтобы получить качественное варение?

4. Ученик купил тетради в клетку и линейку в отношении 2 : 1. Сколько тетрадей в линейку купил ученик, если он купил 24 тетради в клетку?

5. Мама купила сливы и абрикос в отношении 3 : 4. Сколько фруктов каждого вида купила мама, если всего она купила 2 кг 800г фруктов.

6.Торговец продаёт орехи двух сортов: одни по 90 центов, а другие по 60 центов за килограмм. Он хочет получить 50 кг смеси по 72 цента за килограмм. Сколько для этого потребуется орехов каждого сорта?

Решение: пусть х кг – орехов первого сорта, y кг — орехов второго сорта

 Ответ: 20 кг первого сорта и 30 кг второго сорта.

• Модифицированные задачи (МЗ)

1. Вася за неделю получил 18 двоек, даже мама удивилась, просматривая дневник. Двойки Вася получил по математике, истории и литературе в отношении 3: 2: 4 соответственно. Сколько двоек по математике получил Вася за неделю?

2. Число 459 представили в виде суммы трех слагаемых, которые относятся, как 1: 2: 6. Найдите разность между большим и меньшим слагаемыми.

3. В коробке лежат красные и синие кубики, причем отношение числа красных кубиков к числу всех кубиков равно 4 : 11. а) Сколько в коробке синих кубиков, если в ней всего 88 кубиков? б) Сколько в коробке красных кубиков, если в ней 56 синих кубиков?

4. В ящике лежат 99 красных, синих и зеленых шаров. Отношение числа красных шаров к числу синих равно 3 : 2, а числа синих шаров к числу зеленых равно 1 : 3. Сколько находится в ящике шаров каждого цвета?

5. Два брата сложили свои деньги для покупки акций. Старший брат внёс 500 рублей, а младший – 300 рублей. После удорожания акций братья продали свои акции за 1000 рублей. Как они должны поделить деньги между собой?

6.Три семьи решили вскладчину купить дом из 13 комнат за 2600000 рублей. Первая семья хочет иметь 6 комнат, вторая — 4 комнаты, а третья – 3. Сколько денег должен внести каждый из них?

7. В городе имеются три завода по выпуску рыбных консервов. Первый завод может переработать 50 тонн рыбы за трое суток, второй – 45 тонн за двое суток, а третий – 95 тонн за шесть суток. Определите минимальное время, за которое на этих заводах можно переработать 110 тонн рыбы.

Решение:

 110 : 55 = 2 сут.

Ответ: 2 суток.

• Незнакомые задачи (НЗ)

1. разделить 125 на такие 4 части, чтобы первая часть относилась ко второй , как 2:3 , вторая к третей , как 3:5, а третья к четвёртой, как 5:6

2. Первая машинистка может выполнить работу за 10 часов, а вторая – за 15 часов. Как распределить между ними 90 страниц, чтобы они напечатали их в кратчайший срок?

3. Кондитерская производит два вида шоколада с содержанием какао-бобов 25% (молочный) и 70% (горький). В каком отношении надо смешать молочный и горький шоколад, чтобы получился шоколад, содержащий 45% какао-бобов?

Решение: Шоколад % = дробь какао

I х(кг) 25% = 0,25 0,252 ∙ х (кг)

II у(кг) 70% = 0,7 0,7 у (кг)

(х + у) кг 45% = 0,45 0,45 (х + у) кг

Уравнение: 0,25х + 0,7у = 0,45 (х + у)

0,25х + 0,7у = 0,45х + 0,45у

0,7у – 0,45у = 0,45х – 0,25х

0,25у = 0,20х

Ответ: 5 к 4.

4. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20000 рублей, через два года был продан за 15842 рублей.

Решение:

В=15842 руб, А= 20000 руб, n=2.

Воспользуемся формулой , получим:

. = 11(%).

Б З 6: Применение прямой и обратной пропорциональности величин к решению различных задач.

6.1: Задачи на проценты, смеси, сплавы, концентрацию, разбавление.

• Знакомые задачи (ЗЗ)

1. Сколько граммов воды надо добавить к 180 г сиропа, содержащего 25% сахара, чтобы получить сироп, концентрация которого равна 20 %? Ответ: 45 г.

2. Сколько мл воды нужно добавить к 500 мл 96% раствора спирта чтобы получить 40% раствор спирта?

3. Смешали 10% и 25% растворы соли. И получили 3 килограмма 20% раствора. Какое количество каждого раствора в килограммах было использовано?

4. Имеются 200 грамм 30% раствора уксусной кислоты. Сколько грамм воды нужно добавить к этому раствору чтобы получить 6% раствор уксусной кислоты?

5. Из 40 тонн железной руды выплавляют 20 тонн стали, содержащей 6% примесей. Каков процент примесей в руде?

Решение: Пусть в 40 тоннах руды содержится х тонн железа. Тогда ( 40-х) тонн составляют примеси. При выплавке стали количество железа не меняется, а количество примесей уменьшается. Поскольку в 20 тоннах выплавленной стали содержится 94% железа, то х= 0,9420. Вычислим процент примесей в руде:

Ответ:53%

6. Имеется 300 грамм 20% раствора серной кислоты. Сколько граммов воды нужно добавить к этому раствору, чтобы получить 16% раствор серной кислоты?

7. Сплав меди и цинка содержал 82 % меди. После добавления в сплав 18 кг цинка процентное содержание меди в сплаве понизилось до 70%. Сколько меди и сколько цинка было первоначально? Р е ш е н и е.

Решение: Пусть первоначальная масса сплава х кг.

Старый сплав

Новый сплав
медь	Цинк	медь	Цинк
82%		70%
0,82х кг		0,7(х+18)
х кг		( х+18)кг

Расчет ведем по меди, масса меди в сплаве остается неизменной. Получим уравнение 0,82х= 0,7(х+18). Корень уравнения х =105.

Тогда меди в первоначальном сплаве 86,1 кг, цинка – 18,9 кг.

8.Даны два куска с различным содержанием олова. Первый массой 300 г, содержит 20% олова. Второй массой 200 г, содержит 40 % олова. Сколько процентов олова будет содержать сплав, полученный из этих кусков?

Решение:

300 · 0,02 = 60 г — олова в первом сплаве

200 · 0,04 = 80 г — олова во втором сплаве

300 + 200 = 500 г — масса сплава

60 + 80 = 140 г — масса олова в сплаве

140: 500 = 0,28 = 28 %

Ответ: 28 %.

9. При приготовлении маринада для консервирования смешали 10 % и 25 % растворы соли и получили 3 кг 20 % раствора. Какое количество каждого раствора было использовано?

Решение: пусть x кг масса первого раствора, а y кг – второго.

Тогда соли в первом 0,1х, во втором – 0,25y

Масса соли в полученном маринаде: 0,2 · 3 = 0,6 кг

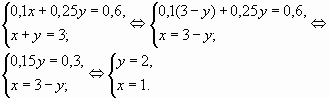
 Ответ: 2 и 1 кг.

10.Соединили два раствора одной и той же кислоты разной концентрации и получили 10 кг нового раствора данной кислоты. Концентрация первого раствора на 10 % больше концентрации второго раствора. Определите массу каждого раствора, если в первом содержалось 0,8 кг кислоты, а во втором – 0,6 кг. Определите процентное содержание кислоты в каждом растворе.

Решение: пусть x кг – масса первого раствора,

y кг — масса второго раствора. В первом – 80/х % кислоты, а во втором – 60/y % кислоты.

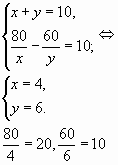
 Ответ: 20 % и 10 %

11. Имеются смеси апельсинового и ананасового соков. Первая смесь содержит 40 % апельсинового сока, а вторая – 80 %. Сливаются вместе p л первой смеси и q л второй смеси, а в результате получается 20 л смеси, содержащей 70 % апельсинового сока. Определите p и q.

Решение:

 Ответ: 5 и 15.

12. Два слитка, один из которых содержит 35% серебра, а другой 65% , сплавляют и получают слиток массой 30 г, содержащий 47 % серебра. Какова масса каждого из этих слитков.

Решение: пусть х г масса первого слитка, а y г – второго слитка.

 Ответ: 18 и 12.

• Модифицированные задачи (МЗ)

1. К раствору. Содержащему 50 г соли, добавили 150 г воды. После этого его концентрация уменьшилась на 7, 5%. Сколько воды содержал раствор и какова была его концентрация?

2. Из сосуда полностью заполненного 12% раствором соли отлили 1 литр и налили 1 литр воды. После этого в сосуде оказался 9% раствор соли. Сколько литров вмещает сосуд?

3. Имеются два сплава, в первом из которых содержится 40%, а во втором -20% серебра. Сколько килограммов второго сплава необходимо добавить к 20 килограммам первого сплава, чтобы получить сплав, содержащий 30% серебра?

4. Соединили два сплава с содержанием меди 40% и 60% и получили сплав, содержащий 45% меди. Найдите отношение массы сплава с 40% содержанием меди к массе сплава с содержанием 60% меди

5. Имеются два слитка сплава золота с медью. Первый слиток содержит 230г золота и 20 г меди, второй слиток содержит 240 г золота и 60 г меди. От каждого слитка взяли по куску , сплавили их и получили 300 г сплава, в котором оказалось 84% золота. Определите массу (в граммах) куска, взятого от первого слитка.

6. Первый  сплав содержит 5% меди, второй – 13% меди. Масса второго сплава больше массы 1-го на 2 кг. Сплавив их вместе, получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.

7. Смешали 42кг и 6кг кислотных растворов разного процентного содержания, получили 40% раствор. Если же смешать равные массы растворов, то получится 50%раствор, Найти массу вещества в первом растворе.

Решение:

 Раствор      % = дробь     Вещество

1   42кг.         х% = 0,01х      0,42х (кг)

2.   6кг           у% = 0,01у      0,06у (кг)   

+    48кг       40% = 0,4       19,2( кг)

Итак, получили уравнение 0,42х  + 0,06у = 19,2

 Раствор      % = дробь      Вещество

1.      1кг              0.01х        0,01х (кг)

2.      1кг              0,01у        0,01у (кг)

+       2кг       50%=0,5         1(кг)

Получаем второе уравнение 0,01х + 0,01у = 1

Решив систему двух уравнений (в нашем случае достаточно найти только х) отвечаем 0,42х =15,4(кг).

                                                           Ответ: 15,4кг  

7.             В лаборатории имеется 2кг раствора, содержащего 28% некоторой кислоты, и 4кг раствора, содержащего 36% этой же кислоты. Найдите наибольшее количество 30%-го  раствора кислоты, который можно получить из этих растворов.

 

Решение: Сначала найдем, в каком отношении надо взять данные растворы по алгоритму, ранее используемому при решении таких задач.

1.   х(кг)     28% = 0,28      0,28х(кг)

2.   у(кг)     36% = 0,36      0,36у(кг)

   (х + у)кг   30% = 0,3        0,3(х + у)кг

Получаем уравнение:

0,28х + 0,36у = 0,3х + 0,3у

0,36у – 0,3у  = 0,3х – 0,28х

     0,06у = 0,02х

          6у = 2х

          3у = х

          х/у =3/1 , то есть данные растворы надо взять в отношении  3 к 1.

 Теперь ответим на вопрос задачи.

1     2кг          3 части

2.     zкг          1часть

      2 :  z  =  3  :  1

          3z  = 2

          z  = 2/3(кг)

       2кг + 2/3 кг = кг      и это ответ на вопрос. 

8.    Один раствор содержит 20 % (по объёму) соляной кислоты, а второй – 70 % кислоты. Сколько литров первого и второго растворов нужно взять, чтобы получить 100 л 50 % раствора соляной кислоты?

Решение:

I – х л ;

II- y л ;

0,2 х кислоты в I растворе

0,7y кислоты во II растворе

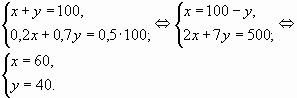
 Ответ: 60 и 40 литров.    

• Незнакомые задачи (НЗ)

1. Имеются два сплава с разным содержанием меди: в первом содержится 70%, а во втором – 40% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 50 % меди?

2. Для приготовления рассола требуется получить солевой раствор. По рецепту раствор нужной концентрации получается, если на 400 грамм воды добавить 100 грамм соли. Сколько грамм соли потребуется чтобы получить солевой раствор нужной концентрации из 1 литра 10% -го солевого раствора?

3. Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 450% олова, а второй 26% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Сплавив 150 кг первого сплава. И 250 кг второго сплава получили новый сплав, в котором оказалось 30% цинка. Сколько килограмм олова содержится в получившемся сплаве?

4. Имеется два сплава золота и серебра. В одном сплаве количество этих металлов находится в отношении 2:3, а в другом – в отношении 3:7. Сколько нужно взять каждого сплава, чтобы получить 8 килограмм нового сплава, в котором золото и серебро были бы в отношении 5:11?

5. Из сосуда, наполненного 96% раствором кислоты, отлили 2,5 литра и долили 2,5 литра 80% раствора той же кислоты, затем ещё раз отлили 2,5 литра и снова долили 2,5 литра 80% раствора кислоты. После этого в сосуде получился 89% раствор кислоты. Найти ёмкость сосуда.

Решение: Пусть емкость сосуда х л. Тогда в нем содержалось л чистой кислоты. Во время первого переливания взяли 2,5 л 96% раствора ( чистой кислоты). В сосуде осталось л кислоты. После этого долили 80% раствор кислоты ( л кислоты). Тогда кислоты стало = л. После этого отлили 2,5 л смеси (или л чистой кислоты). Тогда осталось ()- л кислоты. К ним было добавлено ещё л кислоты и её стало ()-+ 2 л. С другой стороны, известно, что получится 89% раствор кислоты, так как емкость сосуда х л, то в нем содержится л кислоты. Получаем уравнение: ()-+ 2 =. После преобразований получим: 7х²-80х+100=0Корни этого уравнения х=10 и х=0,7 ( не подходит , так, как х >2,5). Итак, ёмкость сосуда 10 л.

6. В куске сплава меди и цинка количество меди увеличили на 40%, а количество цинка уменьшили на 40%. В результате общая масса куска сплава увеличилась на 20%. Определите процентное содержание меди и цинка в первоначальном куске сплава.

 РЕШЕНИЕ:

 Cu    x(кг)      140% = 1,4        1,4х(кг)

 Zn     у(кг)       60% = 0,6        0,6у(кг)

_______________________________

 +     (х + у)кг     120% = 1,2       1,2(х + у)кг

Уравнение: 1,4х + 0,6у = 1,2(х + у)

                      1,4х + 0,6у = 1,2 х +1,2у

                      1,4х – 1,2х = 1,2у – 0,6у

                             0,2х = 0,6у

                                 х = 3у

                                х : у = 3 :1 = 75% : 25%        

                                     

                               Ответ: Cu –  75% ;  Zn – 25%           

7. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?

Решение: рассмотрим решение задачи с помощью метода «стаканов».

Решение:

Х

30%

У

60%

10

0%

Х+у+10

36%

+ + =

Х

30%

У

60%

10

50%

Х+у+10

41%

+ + =

Составим систему уравнений:

3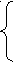0х+60у+10*0=(х+у+10)*36,

30х+60у+10*50=(х+у+10)*41.

Решая ее, получаем х=60, у=30.

Ответ: 60.

Б З 6.2: Задачи на равномерное движение.

• Знакомые задачи (ЗЗ)

1. Трассу, длиной 36 км, один из лыжников прошел на 30 минут быстрее другого. Найдите скорость каждого лыжника, если известно, что скорость первого лыжника на 1км/ч больше скорости второго.

2. Из деревни в город велосипедист проехал за 4 часа. Определить среднюю скорость велосипедиста, если расстояние от деревни до города 60 километров.

3. Первую половину пути, составляющую 18 км, турист проехал на автобусе со скоростью 60 км /час, а вторую прошел пешком. Какова скорость туриста, если на весь путь он затратил 10 часов.

4. Из двух пунктов, расстояние между которыми 38 км отправляются одновременно на встречу друг другу велосипедист и пешеход. Скорость велосипедиста больше скорости пешехода на 10 км/ч. Они встретятся через 3 часа после начала движения. Найдите скорость велосипедиста и пешехода.

5. Из пункта А в пункт В, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 6 часов позже автомобилиста. Ответ дайте в км/ч.

6. Автобус ехал из пункта А до пункта В со скоростью 80 км/ч. Выехав обратно, он 30 км ехал со скоростью, вдвое меньшей первоначальной. Затем он увеличил скорость на 50 км/ч и доехал до пункта А, не меняя скорости. Найдите расстояние от пункта А до В, если на обратный путь водитель затратил на часа меньше.

Решение:

7. Пристани А и В расположены на реке, причем В – на 80 км ниже по течению, чем А. Катер прошел путь из А в В и обратно за 8 ч 20 мин. За какое время катер прошел расстояние от А до В и расстояние от В до А, если известно, что скорость в стоячей воде равна 20 км/ч ?

Р е ш е н и е.

Первый этап.

Составление математической модели.

Пусть х км/ч – скорость течения реки.

V(км/ч)	T=s:v(ч)	S(км)
По течению	20+х	80/20+х	80
Против течения	20-х	80/20-х	80

Получим уравнение

( 80 / 20+х ) + (80/ 20-х ) = 25 / 3

Второй этап. Работа с составленной моделью.

Решив уравнение, находим х = 4.

Третий этап. Ответ на вопрос задачи.

80/24 = 31/3 ч, 80/16 = 5 ч.

• Модифицированные задачи (МЗ)

1 Турист и велосипедист одновременно отправились навстречу друг другу из пунктов А и В. Они встретились через 1,5 ч, после чего каждый продолжил движение в своем направлении. Велосипедист прибыл в пункт А через 2 ч после выезда из В. За какое время прошел путь от А до В турист?

2.Теплоход скорость которого в стоячей воде равна 25 км/ ч проходит по течению реки и после 5часовой стоянки возвращается в исходный пункт. Скорость течения реки 3км/ч. От отплытия до возвращения в исходный пункт прошло 30 часов. Сколько км прошел теплоход за весь рейс.

3. Два велосипедиста выехали из пункта в пункт В с одинаковой скоростью, превышающей 5 км/ч. Проехав треть всего пути, первый велосипедист не меняя скорости вернулся в пункт А, пробыл в нем 22 минуты и снова поехал в пункт В, увеличив скорость на 3 км/ч. С какой скоростью ехал второй велосипедист, если в пункт В он приехал на 1 час 30 минут раньше первого. Расстояние между пунктами равно 26 километров.

4. Катер проплыл против течения реки 20 километров и 14 километров по течению реки. На весь путь он затратил 3 часа. Найдите скорость течения реки, если скорость катера в стоячей воде равна 12 км/ч.

5. Первый  сплав содержит 5% меди, второй – 13% меди. Масса второго сплава больше массы 1-го на 2 кг. Сплавив их вместе, получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.

6. Электричка проходит мимо столба за 8секунд.

 За какое время (в секундах) пройдут мимо друг друга пассажирский поезд и электричка, если скорость пассажирского поезда равна скорости электрички, а длина пассажирского поезда в полтора раза больше длины электрички?

Решение:
v t s

Э.п (м/с) 8с х(м)

П.п. (м/с) 1,5х(м)

s = х +1,5х = 2,5х(м) ; v =

t = 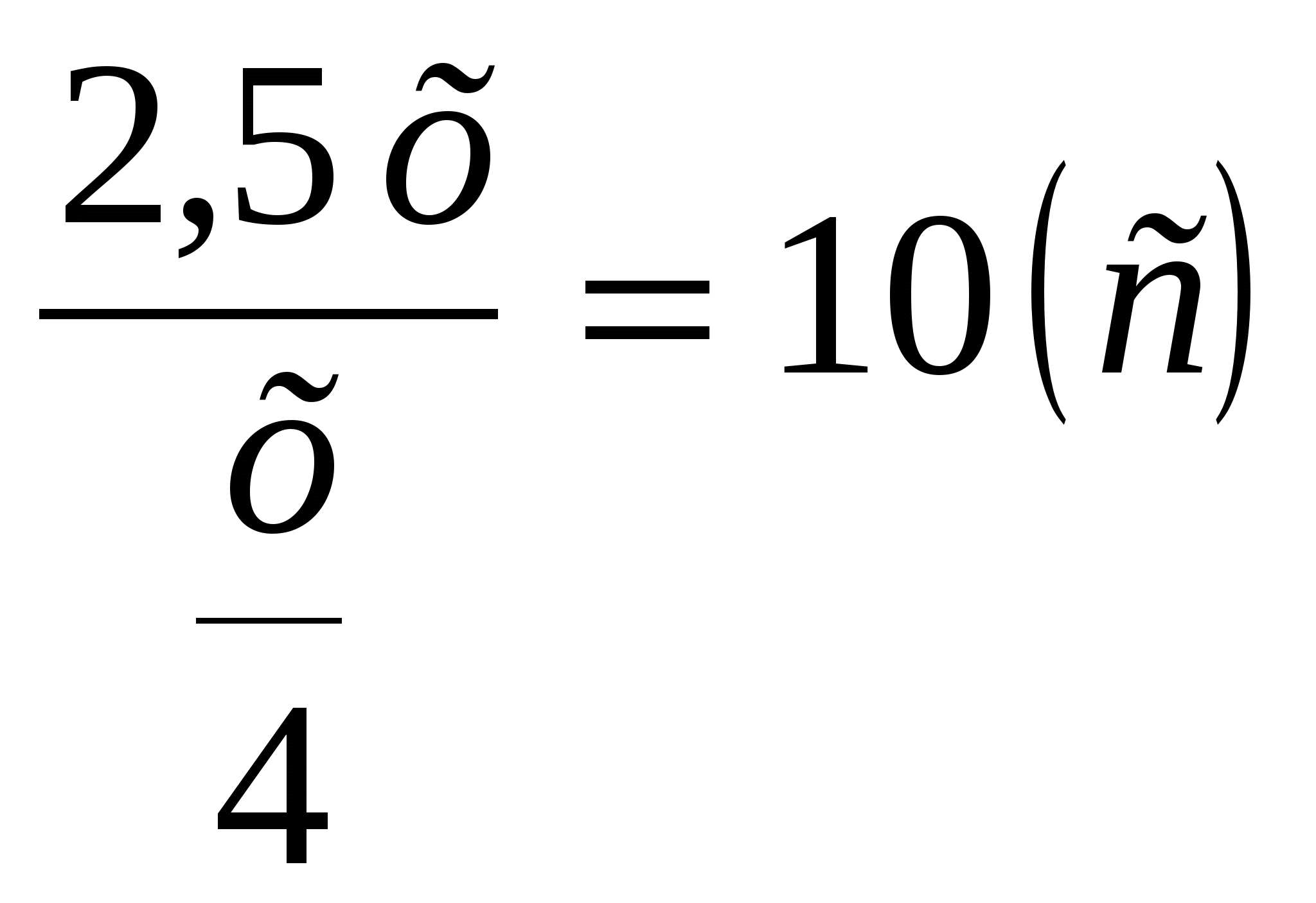и это ответ.

6. Грузовик едет сначала 3 минуты с горы, а затем 7 минут в гору. На обратный путь он тратит 22 минуты. Во сколько раз скорость грузовика при движении с горы больше, чем его скорость при движении в гору?

Решение: v(км/ч)             t(ч)               s(км)

 С горы           х                                        s

 В гору            у                                         s

Уравнение: 

 С горы            х               

 В гору              у                 

Уравнение:  

 Решим систему двух уравнений.

  Решив это уравнение, получим  корни его    и   7

 Условию задачи удовлетворяет корень 7.

  Ответ: скорость с горы в 7 раз больше, чем в гору.              

7. Расстояние между двумя городами скорый поезд проходит на 4 часа быстрее товарного и на 1 час быстрее пассажирского. Найти скорости товарного и скорого поездов, если известно, что скорость товарного поезда составляет 5/8 от скорости пассажирского и на 50 км/ч меньше скорости скорого. Решение: Пусть х, км/ч – скорость товарного поезда (х>0), у, ч – время движения скорого поезда (у>0).Составляем таблицу.

Величины

Процессы

Расстояние (км)	Скорость (км/ч)	Время (ч)
Скорый поезд	(х+50)у	х+50 ?	у
Пассажирский поезд	8/5 х(у+1)	8/5 х	у+1
Товарный поезд	х(у+4)	х ?	у+4

По условию задачи поезда прошли одно и то же расстояние. Получаем систему уравнений

8/5 х(у+1) = х(у+4)

(х+50)у = х(у+4).

По условию задачи х>0, тогда

8(у+1) = 5(у+4)

(х+50)у = х(у+4),

3у = 12

(х+50)у = х(у+4),

у = 4

х+50 = 2х,

у = 4

х = 50.

Полученные значения неизвестных удовлетворяют условию х>0, у>0, значит удовлетворяют условию задачи.

50 км/ч – скорость товарного поезда.

50+50 = 100 (км/ч) – скорость скорого поезда.

Ответ: 50 км/ч, 100 км/ч.

• Незнакомые задачи (НЗ)

1 Пловец плывет против течения реки и встречает по пути плывущую по течению пустую лодку. Он продолжает плыть еще m минут после встречи против течения, а затем поворачивает назад и догоняет лодку в s метрах от места встречи. Найдите скорость течения реки.

2.Два гонщика стартуют одновременно из одной точки трека, имеющего форму окружности, едут в одном направлении с постоянными скоростями. Первый гонщик , сделав 9 кругов, впервые догоняет второго в точке старта. Еще через 0,5 часа он обогнал второго уже на 1,5 круга после старта. Сколько кругов в час делает каждый гонщик?

3. Два судна движутся прямолинейно и равномерно в один и тот же порт. В начальный момент времени положение судов и порта образует равносторонний треугольник. После того как второе судно прошло 80 км, указанный треугольник становится прямоугольным. В момент прибытия первого судна в порт второму остается пройти 120 км. Найти расстояние между судами в начальный момент времени.

Решение: Пусть первое судно находилось в точке А ,

Второе судно в точке В,

Порт в точке С.

Треугольник АВС – равносторонний , где АВ – расстояние между суднами -?

Пусть V₁ скорость первого судна

V₂— скорость второго судна V₁>V₂ (так как первое судно добралось раньше)

Второе судно до точки Е прошло 80 км, первое судно оказалось в точке Д

Треугольник СДЕ — прямоугольный ‹ Д= 90 ‹С=60 ⁰ ‹Е=30

СД = или 2СД= ЕС. Вычислим ЕС. ЕС= ВС-ВЕ=S-80.

Второе судно прошло 80км за время , Первое судно прошло АД= V₁.

Тогда СД = АД- АВ= S— V₁.

2СД= ЕС, значит 2S—=S-80 или S+80=, когда первое судно пришло в порт С , второе находилось в точке F. t₁= ; CF =120км BF=BC—CF= S-120 (потратив время ч.) Приравняем эти два времени и получим уравнение = или . Имеем систему уравнений : . В этой системе три неизвестные величины: S, V₁,V₂. Соотношение из первого уравнения подставим во второе, преобразуем его и получим S²-200S-9600=0 . Корни этого уравнения : S= 240 км S=-40(П.К) из первого уравнения системы можно найти отношение скоростей судов, оно равно 2. Итак, первоначальное расстояние между судами S = 240км.

4. Два тела, двигаясь по окружности в одном и том же направлении, встречаются через каждые 56 мин. Если бы они двигались с теми же скоростями в противоположных направлениях, то встречались бы через каждые 8 мин. Если при движении в противоположных направлениях в некоторый момент времени расстояние по окружности между телами равно 40 м, то через каждые 24 с оно будет 26 м (в течение этих 24 с тела не встретятся). Найдите скорости тел и длину окружности.

Решение: Решение:

Пусть l м – длина окружности,

х м/мин — скорость первого тела, а у м/мин – скорость второго тела (х > у).

В задаче речь идет о трех ситуациях, каждую из которых можно описать уравнением.

А). При движении в одном направлении первое тело догоняет второе со скоростью (x – y) м/мин. После одного из обгонов следующий обгон имеет место через столько минут, сколько понадобиться, чтобы преодолеть l метров со скоростью (x – y) м/мин, т.е. через 56 мин:

l/х-у=56 (1)

Б).При движении в разных направлениях тела сближаются со скоростью (x + y) м/мин, причем l м они вместе проходят за 8 мин l/ х+у = 8 (2)

Если первоначальное расстояние было равно 40м, осталось пройти до встречи 26 м, то общий путь составляет

40м – 26м = 14м.

Он был преодолен со скоростью (x + y) м/мин за 24 с, т.е. за 24/60 мин, что равно 2/5 мин.

Следовательно последняя часть условия приводит к уравнению 14/х+у=2/5 (3)

Разделив уравнение (2) на (1), получим

х-у/х+у = 1/7 , отсюда у = 3/4 х

Решим систему уравнений

у = ¾ х

14/х+у =2/5

Следовательно, у = 15, а из уравнения (2) l = 280.

Ответ: 280 м, 20 м/мин, 15 м/мин.

5. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?

Решение:

Будем считать, что первый сухогруз неподвижен, а второй приближается к нему со скоростью х(м/мин), равной разности скоростей второго и первого сухогрузов. Тогда за 12 минут второй сухогруз проходит расстояние

L=400+80+120+600=1200 (м). Поэтому х=1200/12=100 (м/мин), то есть 6 (км/час).

Ответ: 6

Б З 6.3: Задачи на работу.

• Знакомые задачи (ЗЗ)

1 Один комбайн может убрать все поле за 6 дней, а другой – за 4 дня. Какую часть поля уберут оба комбайна за один день?

2. Две бригады должны были выполнить заказ за 12 дней. После 8 дней совместной работы первая бригада получила другое задание, поэтому вторая бригада заканчивала выполнение заказа еще 7 дней. За сколько дней могла бы выполнить заказ каждая из бригад, работая отдельно.

3. Одна тракторная бригада должна вспахать 240 га, а другая на 35% больше, чем первая. Первая бригада, вспахивая ежедневно на 3 га меньше второй, закончила работу на 2 дня раньше, чем вторая бригада. Сколько гектаров вспахивала каждая бригада ежедневно?

 Р е ш е н и е. Найдем 35% от 240 га: 240 га ? 35%/100%=84 га. Следовательно, вторая бригада должна была вспахать 240 га+84 га=324 га. Пусть первая бригада вспахивала ежедневно х га. Тогда вторая бригада вспахивала ежедневно (х+3) га; 240/х – время работы первой бригады; 324/(х+3) – время работы второй бригады. По условию задачи первая бригада закончила работу на 2 дня раньше, чем вторая, поэтому имеем уравнение 324/(x+3)-240/x=2

которое после преобразовании можно записать так: 324x-240x-720=2×2+6x

2×2-78x+720=0

X2-39x+360=0

Решив квадратное уравнение, находим х1=24, х2=15. Это норма первой бригады. Следовательно, вторая бригада вспахивала в день 27 га и 18 га соответственно. Оба решения удовлетворяют условию задачи.

О т в е т: 24 га в день вспахивала первая бригада, 27 га – вторая; 15 га в день вспахивала первая бригада, 18 га – первая.

4. В городе есть водоем. Одна из труб может заполнить его за 4 часа, вторая – за 8 часов, а третья – за 24 часа. За сколько времени наполнится водоем, если открыть сразу 3 трубы?

Решение задачи:

1. 1: 4 = (водоема) наполнится через 1 трубу за 1 час;

2. 1 : 8 = (водоема) наполнится через 2 трубу за 1 час;

3. 1 : 24 = (водоема) наполнится через 3 трубу за 1 час;

4. (водоема) наполнится через 3 трубы за 1 час;

5. (часа) время наполнения водоема через 3 трубы.

Ответ: через 3 трубы, работающие одновременно, водоем наполнится за часа.

• Модифицированные задачи (МЗ)

1 На изготовление 21 детали первый рабочий затрачивает на 4 часа меньше, чем второй рабочий на изготовление 35 таких же деталей. Известно. Что первый рабочий за час делает на 2 детали больше, чем второй. Сколько деталей в час делает второй рабочий?

2.Две машинистки должны были напечатать по 60 страниц каждая. Вторая машинистка печатала за 1 час на 2 страницы меньше, поэтому закончила работу на 1 час позже. Сколько страниц в час печатала первая машинистка?

3.Два пешехода вышли одновременно из двух поселков навстречу друг другу. Один пешеход может пройти весь путь за 3 часа, а другой – за часа. Через сколько времени они встретятся?

Решение задачи: это тоже задача на “совместную работу”, хотя никто не работает. Но можно считать, что “работа” пешеходов – это прохождение пути. Поэтому весь путь принимается за “единицу” и вычисляется часть пути, пройденная каждым пешеходом.

1. 1: 3 = (расстояния) проходит 1 пешеход за 1 час;

2. 1 : (расстояния) проходит 2 пешеход за 1 час;

3. (расстояния) сближаются оба пешехода за 1 час;

4. (часа) пешеходы встретятся.

Ответ: через часа.

4. Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 8 вопросов теста, а Ваня — на 9. Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Вани на 20 минут. Сколько вопросов содержит тест?

Решение: Не смотря на то, что в задаче сказано, что мальчики выполняли тест одновременно, это все-таки задача на раздельную работу – одновременно, как легко догадаться, в этом случае не означает вместе.

Из условия получаем, что «производительность» Пети – 8 вопросов в час, а Вани – 9 вопросов в час.

Пусть тест содержит х вопросов, тогда Петя ответит на него за часа, а Ваня за .

По условию задачи Петя закончил свой тест позже Вани на 20 минут, то есть он выполнял тест на часа дольше Вани.

Получим уравнение:

Отсюда:

Ответ: 24

5.Двое рабочих выполнили вместе некоторую работу за 12 ч. Если бы сначала первый рабочий сделал половину этой работы, а затем другой остальную часть, то вся работа была бы выполнена за 25 ч. За какое время мог бы выполнить эту работу каждый рабочий в отдельности?

Р е ш е н и е.

Первый этап. Составление математической модели.

N=A:t	T(ч)	A
1	1/х	х	1
2	1/у	у	1

Примем всю работу за 1.Производительность труда I рабочего 1/х , а II – 1/у . За 12 ч, работая отдельно, I рабочий выполнит ( 1/х)·12 всей работы, а II рабочий –(1/у) ·12

всей работы, т.е. 12/х + 12/у = 1

х/2ч-время, которое потребуется 1 рабочему, чтобы сделать половину работы, у/2ч- время, которое потребуется 2 рабочему, чтобы сделать половину работы, тогда х/2+у/2=25.

Второй этап. Работа с составленной моделью.

12/х + 12/у = 1

х/2+у/2=25.

находим решение: х = 20, у = 30 .

Третий этап. Ответ на вопрос задачи. 20 ч и 30 ч.

6. Первый наборщик текста набирает за час 5 страниц текста, второй – 6 страниц, а третий – 7 страниц. Определите, по сколько страниц текста нужно отдать для набора каждому из них, если требуется, чтобы весь текст, объем которого 216 страниц, был набран как можно быстрее.

Решение:

5 + 6 + 7 = 18 частей всего

216 : 18 = 12 страниц 1 часть

12 · 5 = 60 стр.

12 · 6 = 72 стр.

12 · 7 = 84 стр.

Ответ: 60, 72, 84 страницы.

• Незнакомые задачи (НЗ)

1. Для откачивания воды из резервуара имеется четыре насоса. Если включить первый , второй и третий насосы, то работа будет выполнена за 10 мин; если включить первый, третий и четвертый насосы, то та же работа будет выполнена за 12 мин. Если же будут работать только второй и четвертый, то за 15 мин. За какое время можно откачать воду из резервуара при помощи всех четырех насосов?

2. Грузчики Петр и Владимир вместе могут перенести 22 ящика с гвоздями со склада в торговый зал за 40 минут, Михаил и Петр могут перенести 30 таких же ящиков за 50 минут, а Владимир и Михаил – 41 ящик за час. За сколько минут Петр, Владимир и Михаил перенесут 22 ящика, работая втроем?

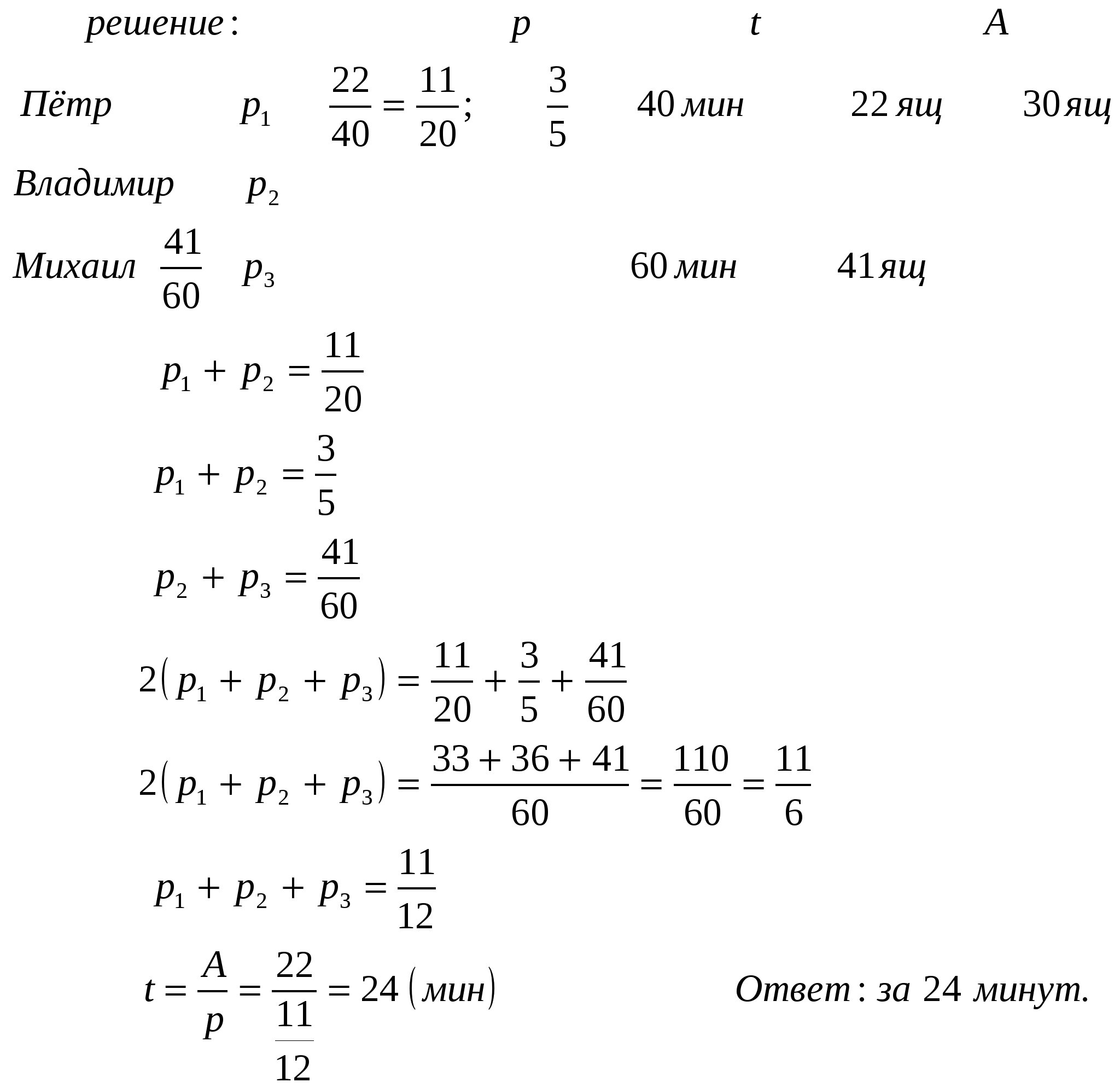
3. Бассейн наполняется двумя трубами, действующими одновременно, за 2 часа. За сколько часов может наполнить бассейн первая труба, если она, действуя одна, наполняет бассейн на 3 часа быстрее, чем вторая?

Решение:

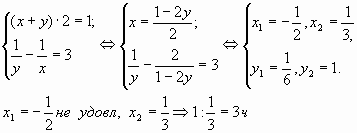
Ответ: 3 часа.

Б З 6.4: Задачи на запись чисел.

• Знакомые задачи (ЗЗ)

1 Купили 5 одинаковых коробок карандашей. Может ли в них оказаться: всего 92 карандаша? 90 карандашей?

2.Сумма цифр двузначного натурального числа равна 14. Если к этому числу прибавить 46, то получиться число , произведение цифр которого равно 6. Найдите это число.

3. Разность цифр двузначного числа равна 2, а сумма квадратов этих же цифр равна 52. Найдите это число.

4. Найдите двузначное число , которое в 7 раз больше суммы его цифр и в 3,5 раз больше произведения его цифр.

5.Если двузначное число разделить на сумму его цифр , то получится число 2. Если же это число разделить на произведение его цифр, то получиться 2,25. Найдите это число.

6. Сумма кубов цифр двузначного числа равна 91, а произведение суммы цифр на произведение цифр равно 84. Найдите это число.

• Модифицированные задачи (МЗ)

1 Для поездки за город работникам завода был выделено несколько автобусов, с одинаковым числом мест в каждом автобусе. В лес поехали 424 человека, а на озеро – 477 человек. Все места в автобусе были заняты, и ни одного человека не осталось без места. Сколько автобусов было выделено и сколько пассажиров было в каждом автобусе? Ответ: 17 автобусов по 53 пассажира.

2. Найдите двузначное число, если количество единиц в нём на 4 больше количества десятков. А произведение искомого числа на сумму его цифр равно 90.

3. В контейнере находятся коробки и ящики общим числом более 16. Если вдвое увеличить количество коробок и на 20 – количество ящиков , то ящиков будет больше , чем коробок. Если же , не меняя количество коробок, удвоить количество ящиков , то их будет всё- таки меньше , чем коробок. Сколько коробок было в контейнере?

• Незнакомые задачи (НЗ)

1 Доказать, что трехзначное число состоит из одинаковых цифр и делится на 37.

Ответ: с =100с + 10с + с = 111с = 3 * 37с.

2. Натуральное число nри делении на 5 даёт остаток 3. Найти остаток от деления на 5 квадрата числа n.

Решение: Так как n при делении на 5 даёт остаток 3 , то его можно записать в виде : n=5k+3( где k— частное).N=n²=(5k+3)²= 25k²+30k+9. Выделим в числе N слагаемые , которые без остатка делятся на 5 : 25k²и30k. В числе 9также выделим число, которое делится на 5 : 9= 5=4. Тогда число N=(25k²+30k+5)+4= 5(5k²+6k+1)+4.Значит при делении числа Nна 5 получается остаток 4.

3.Доказать , что при любом натуральном n выражение N= n²—n делится без остатка на 6.

4.Является ли число 535353…53 простым?( количество цифр в числе — 120)

Решение: Используя признаки делимости на 2;4; 5; 8; 10 видим что ни на одно из этих чисел данное число не делится. Проверим признаки делимости на 3 и 9. Для этого найдём сумму цифр числа. Число образовано повторяющейся группой цифр 53 и таких групп 60, то сумма цифр числа (5+3)*60=480. Эта сумма делится на 3, поэтому данное число тоже делится на 3, т.е. является составным.

5. Если некоторое двузначное число умножить на сумму его цифр, то получится 405. Если число, написанное теми же цифрами в обратном порядке, умножить на сумму его цифр, то получится 486. Найти это число.

Решение: Пусть дано некоторое двузначное число n, у которого а- количество десятков, в- количество единиц. Тогда n= 10а+в. Число , записанное в обратном порядке ( 10в+а). записав условие задачи , получим систему

Разделив уравнения друг на друга, будем иметь: , откуда в= . Тогда а²=16. ( а₁=4; а₂=-4)Отрицательный корень не подходит, т.к. а>0. Тогда в= 5. Искомое число 45.

6.Доказать , что разность между трёхзначным числом и и числом записанным в обратном порядке этими же цифрами , делится без остатка на 9.

Примеры решения текстовых задач на движение (разложение решения по базису с учётом СУД и УУД).

Два велосипедиста выехали из пункта А в пункт В с одинаковой скоростью, превышающей 5км/час. Проехав треть всего пути, первый велосипедист, не меняя скорости, вернулся в пункт А, пробыл в нём 22 минуты и снова поехал в пункт В, увеличив скорость на 3км/час. С какой скоростью ехал второй велосипедист, если в пункт В он приехал на 1 час 30 минут раньше первого. Расстояние между пунктами равно 26км.

Решение: пусть V₁=V₂ скорости велосипедистов. V₁> 5- по условию. Тогда t₂=— время второго велосипедиста от А до В, 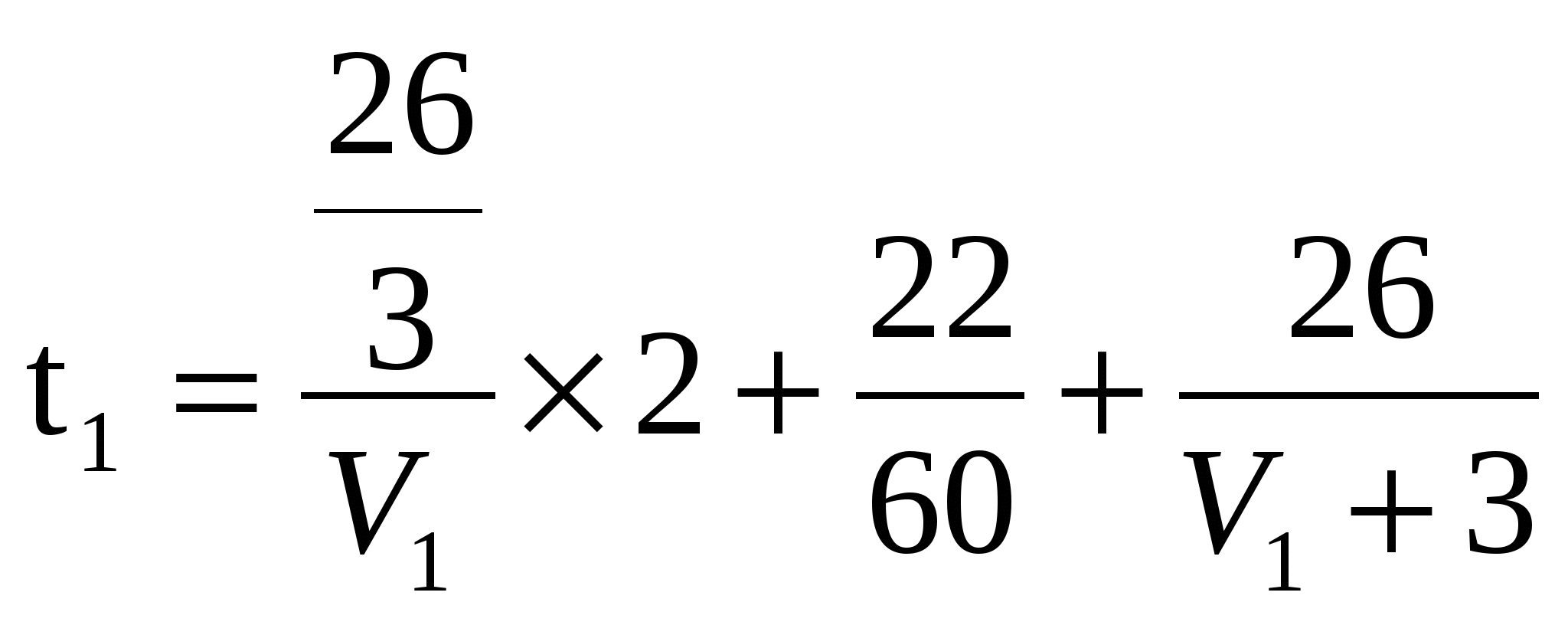— время движения первого велосипедист а от А до В. Приравняв получим уравнение

. После преобразования получим .Далее получим квадратное уравнение 17V₁²-209 V₁+390= 0 его корнями будут числа 10 и , второй корень не подходит условию задачи V₁> 5, следовательно, второй велосипедист ехал со скоростью 10 км/ч

Решение задачи

Специальные учебные математические действия (СУД)	Специальные учебные математические действия (УУД)
Введение обозначения V1=V2	Введение обозначения	Выделение существенной информации, абстрагирование Знаково-символические действия
ограничение: V1> 5	Перевод текста в математические соотношения	Знаково-символические действия
привлекая закон движения, получим модель: t2= время второго движения велосипедиста	Привлечение из физики известного закона движения с постоянной скоростью s = vt; где S -пройденный путь., v скорость, t — время движения. Здесь величина S прямо пропорциональна v и t . В t2= имеет место обратно- пропорциональная зависимость времени и скорости	Анализ ситуации, поиск аналога. корректировка аналога и его конкретизация, знаково-символические действия (в том числе интерпретация полученных соотношений в терминах условия задачи)
время движения первого велосипедист а от А до В.	Добавить стоянку 22 мин, и увеличение скорости на 3 км/час	Всё сказанное выше
Приравняв с учетом условия время движения, получим основное уравнение задачи	Поиск инварианты времени, возможность приравнять время первого и второго с корректировкой, получение уравнения с одним неизвестным	Анализ, выделение существенной информации, выведение следствий, синтез, построение основной мат. модели задачи, знаково-символические действия, выдвижение гипотезы
приводим уравнение к виду	Приведение подобных, преобразование алгебраических дробей	Анализ. синтез, поиск аналогов, проверка гипотезы, выполнение действий по инструкции, сверка результата и эталона, оценка
получим квадратное уравнение 17V12-209 V1+390= 0	Приведение к общему-знаменателю, приведение подобных, отбрасывание знаменателя с наложением ограничений	Всё сказанное выше
корнями будут числа 10 и	Применение стандартного алгоритма решения квадратного уравнения	Всё сказанное выше
второй корень не подходит условию задачи V1> 5	Проверка условия, выписанного в начале решения	знаково-символические действия (в том числе интерпретация полученных соотношений в терминах условия задачи), проверка гипотезы.
второй велосипедист ехал со скоростью 10 км/ч	Сопоставить начало и конец решения задачи, проверить, есть ли неучтенные ограничения; ответ давать словами вопроса задачи {если нужно. слегка отредактировав вопрос).	Анализ, синтез, изменение угла зрения, контроль, оценка, сравнение с эталоном, подтверждение правильности гипотезы
Исследование, варьирование параметров задачи	Перестраивание модели, основного уравнения задачи	Анализ, синтез, изменение угла зрения, выдвижение гипотез, абстрагирование, конкретизация, обобщение

Заключение

При решении текстовых задач учащимся могут помочь несколько простых и общих советов.

Совет 1. Не просто прочитайте, а тщательно изучите условие задачи. Попытайтесь полученную информацию представить в другом виде – это может быть рисунок, таблица или просто краткая запись условия задачи.

Совет 2. Выбор неизвестных.

В задачах «на движение» – это обычно скорость, время, путь. В задачах “на работу” — производительность и т.д.

Не надо бояться большого количества неизвестных или уравнений. Главное, чтобы они соответствовали условию задачи и можно было составить соответствующую “математическую модель” (уравнение, неравенство, система уравнений или неравенств).

Совет 3. Составление и решение “математической модели”.

При составлении “математической модели” (уравнения, неравенства, системы уравнений или неравенств) ещё раз внимательно прочитайте условие задачи. Проследите за тем, что соответствует каждой фразе текста задачи в полученной математической записи и чему в тексте задачи соответствует каждый “знак” полученной записи (сами неизвестные, действия над ними, полученные уравнения, неравенства или их системы).

Очень важно не только составить уравнение, неравенство, систему уравнений или неравенств, но и решить составленное.

Если решение задачи не получается, то нужно ещё раз прочитать и проанализировать задачу (заданный текст и полученную запись).

Иногда по условию задачи достаточно отыскать не сами неизвестные, а их комбинации. Например, не x и y, а x+y, x/y, 1/x и т.п.

Если кажется, что получилось правильное, но очень сложное выражение, то попробуйте ввести другие неизвестные, может быть, изменив их количество, чтобы получилась более простая модель.

Иногда неизвестные в задачах выражаются только целыми числами, тогда при решении задач нужно использовать свойства целых чисел.

Совет 4. Решение сложной текстовой задачи – процесс творческий. Иной раз требуется вернуться к самому началу задачи, учитывая и анализируя уже полученные результаты.

При решении задач короткую запись задачи можно сделать с помощью рисунка или таблицы.

Таблица является универсальным средством и позволяет решать большое количество идейно близких задач.

Выводы:

• Для того, чтобы научиться решать задачи, надо приобрести опыт их решения путем многократного повторения операций, действий, составляющих предмет изучения.

• Редкие ученики самостоятельно приобретают такой опыт. Долг учителя — помочь учащимся приобрести опыт решения задач, научить их решать задачи.

• Помощь учителя не должна быть чрезмерной, но и не быть слишком малой.

• Навыки решения текстовых задач формируются на основе осмысленных знаний и умений.

• Для формирования навыков нужна тщательно продуманная многоуровневая система задач «от простого к сложному».

• Знания учащихся по математике должны совершенствоваться с решением каждой новой задачи.

• Следует добиваться, чтобы осознанные умения и навыки ученики получали при наименьших затратах времени.

• Следует учитывать индивидуальные особенности и возможности учащихся.

Список литературы

1. Аверьянов Д.И., Алтынов П.И., Баврин И.И. Математика: Большой справочник для школьников и поступающих в вузы. – М.: Дрофа, 1998.-864с.: ил.

2. Максютин А.А., Шаповалова Т.П. Методическое обеспечение подготовки учителей математики к введению профильного обучения – Самара, 2008

3. Ерина Т.М. Алгебра. Текстовые задачи — Москва, МГТУ «МАМИ»,2004

4. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.-,Алгебра 9класс ,Москва, Просвещение, 2009

5. Методика преподавания математики в средней школе: общая методика А.Я.Блох и другие, Москва, Просвещение, 1985.Мордкович А.Г. -.Алгебра 9класс, Москва, Мнемозина, 2009

6. Примерные программы по учебным предметам. Математика .5 -9 классы проект- Москва, Просвещение, 2010 (Стандарты второго поколения)

7. Турецкий Е.Н., Фридман Л.М. -Как научиться решать задачи, Москва, Просвещение, 1989

8. Презентационные подходы в решении текстовых задач. https://school-collection. edu.ru/.

9. Максютин А.А. Многоуровневая система задач как средство обучения учащихся средней школы алгебре и началам математического анализа: диссертация кандидата педагогических наук: 13.00.02. — Самара, 2007. — 324 с.: ил. РГБ ОД, 61:07-13/2006

10. Епишева О.Б. Методическая система обучения математике на основе формирования приёмов учебной деятельности. Тобольск, 1999.-176

11. Епишева О.Б. Технология обучения математике на основе деятельностного подхода. М.: Просвещение, 2003. 224 с.

12. Иванюк М.Е., Липилина В.В., Максютин А.А. Проблемы реализации ФГОС при обучении математике в основной и старшей общеобразовательной школе. Монография. Самара 2014.

13. Шевкин, А. В. Материалы курса “Текстовые задачи в школьном курсе математики” [Текст]: лекции 5-8. / А. В. Шевкин – М.: Педагогический университет “Первое сентября”, 2006. – 80 с

14. Методика преподавания математики в средней школе: общая методика А.Я.Блох и другие, Москва, Просвещение, 1985.

15. Турецкий Е.Н., Фридман Л.М. -Как научиться решать задачи, Москва, Просвещение, 1989

16. Решение текстовых задач. https://school-collection.edu.ru/catalog/res/d92c7ae3-a9f1-4ff3-afb0-e1f1783fee48/?from=8f5d7210-86a6-11da-a72b-0800200c9a66&.