Хостинг документов » 10 класс » Проблемное обучение на уроках математики

Проблемное обучение на уроках математики

Муниципальное общеобразовательное учреждение

Средняя общеобразовательная школа № 67

с углубленным изучением отдельных предметов

г.Екатеринбурга Свердловской обласи

подготовила

учитель математика

Ковалева Нина Петровна

г. Екатеринбург

2013

Традиционно цели школьного образования определялись набором знаний, умений, навыков, которыми должен владеть выпускник. Сегодня такой подход оказался недостаточным, поскольку существует объективная необходимость применения новых методов обучения, которые позволят формировать творческих знающих специалистов, способных самостоятельно решать научные проблемы. Способствуют достижению поставленных задач использование технологии проблемного обучения на уроках.

Цель проблемного обучения – это не только усвоение результатов научного познания, системы знаний, но и самого пути процесса получения этих результатов, формирования познавательной самодеятельности ученика и развития его творческих способностей.

Проблемное обучение не сводится к тренировке учащихся в умственных действиях. Цель активизации путем проблемного обучения состоит в том, чтобы поднять уровень усвоения учащимися понятий и обучить не отдельным мыслительным операциям в случайном, стихийно складывающемся порядке, а системе умственных действий для решения нестереотипных задач. Эта активность заключается в том, что ученик, анализируя, сравнивая, синтезируя, обобщая, конкретизируя фактический материал, сам получает из него новую информацию. Другими словами, это расширение, углубление знаний при помощи ранее усвоенного и новое применение прежних знаний. Новому применению прежних знаний не могут научить ни книга ни учитель – это ищется и находится учеником, поставленным в соответствующую ситуацию.

Все виды проблемного обучения характеризуются наличием репродуктивной, продуктивной и творческой деятельности ученика, наличием поиска и решения проблемы. Они могут осуществляться при различных формах организации педагогического процесса. Эффективным может считаться такой процесс обучения, который обусловливает:

— увеличение объема знаний, умений и навыков учащихся;

— углубление и упрочение знаний, новый уровень обученности и воспитанности;

— новый уровень познавательных потребностей учения;

— новый уровень сформированности познавательной самостоятельности и творческих способностей.

Как появляется проблемная ситуация в обучении? Возникает ли она непроизвольно или создается учителем?

В литературе по проблемному обучению встречаются два понятия: «возникновение» и «создание» проблемных ситуаций. Во-первых, для ученика проблемная ситуация всегда возникает, для учителя учебных проблемных ситуаций нет, могут быть только педагогические затруднения. Во-вторых, проблемная ситуация порождается учебной или практической ситуацией, логикой учебного предмета или логикой процесса. По логике учебного предмета они возникают, как правило, независимо от желания учителя, т.е. объективно. Проблемные ситуации могут создаваться учителем преднамеренно, если он знает правила организации проблемного обучения.

Целенаправленное использование учителем проблемных ситуаций, возникающих помимо его желания (объективно), и ситуаций, преднамеренно им создаваемых, представляют собой систему, умелое применение которой и является основной особенностью проблемного обучения.

Способы создания проблемных ситуаций на уроках математики:

I. Использование учебных и жизненных ситуаций, возникающих при выполнении учащимися практических заданий. Проблемные ситуации в этом случае возникают при попытке учащихся самостоятельно достигнуть поставленной цели. Обычно ученики в итоге анализа ситуации сами формулируют проблему.

Пример 1. На уроке геометрии по теме «Длина ломаной» ученикам предложена практическая работа в двух вариантах: начертить ломаную (В-I из двух звеньев, В-II из трех звеньев) путем измерения сравнить длину ломаной с расстоянием между ее концами. Результаты у всех, естественно разные. Учитель выписывает их в две колонки на доске.

Длина ломаной Расстояние между концами

15 см. 13 см.

08 см. 6,5 см.

11,3 см. 10 см.

Ученикам предлагается внимательно рассмотреть числа и сделать предположение и зависимости между длиной ломаной и расстоянием между ее концами. После высказывания предположений ищут пути решения проблемы и переходят к доказательству в общем виде.

Пример 2. 9 класс геометрия, тема «Сложение векторов». Тему начать с выполнения практического задания: даны a и b, т. M и N (каждый выбирает сам).

Найти образы точек M и N при композиции векторов, то есть M₂= b( a (M)),

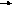
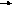
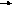
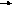
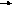
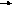
N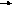₂=b( a (N)). Какое преобразование пространства вместо b * a можно было выполнить, чтобы M M, N N? Какое предположение о этих преобразованиях пространства можно высказать? Затем выдвигается гипотеза (обоснованное предположение) о композиции двух векторов: b * a = c.

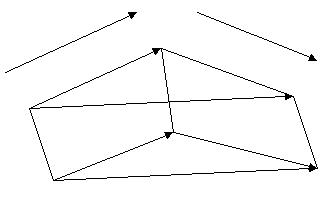
Пример 3. 11 класс алгебра тема «Логарифмирование». До сообщения темы дается самостоятельная работа практического характера. С помощью графика функции y=lg x найти значения lg 1,5; lg 4 и lg 6. Сравнить значение выражений lg 1,5 + lg 4 и lg (1,5*4). После проверки результатов (на доске заранее выписаны выражения из различных вариантов) учащиеся выдвигают гипотезу lg a+lg b= lg (ab), a>0, b>0.

II. Побуждение учащихся к теоретическому объяснению явлений, фактов, внешнего несоответствия между ними. Это вызывает поисковую деятельность учеников и приводит к активному усвоению новых знаний.

Пример 1. 7 класс геометрия тема: «Сумма внутренних углов треугольника». Перед изучением теоремы ученикам предлагается построить треугольник по трем заданным углам. Учащиеся знают, что это возможно и умеют выполнять такие задания. В предлагаемом задании: 1) ∟А=90°, ∟B=60°, ∟С=45°. 2) ∟А=70°, ∟B=30°,∟С=50°. Как бы точно ученик не откладывал требуемые величины заданных углов, он не может построить треугольник. Перед ним возникает проблема: «Почему в предлагаемых заданных нельзя построить треугольник, несмотря на то, что известны величины трех углов?» У ученика возникает потребность в познании изучаемого закона. В результате поставленного задания усваивание учеником знания предстает перед ним, как требуемое неизвестное знание. Теперь изучение указанной теоремы индуктивным или дедуктивным путем будет составлять для ученика открытие нового.

Пример 2. 11 класс алгебра и начала анализа тема «Иррациональные уравнения». Дается задание: проверьте может ли число 5 быть корнем иррационального уравнения √х-6=√4-х ? (нет, при х=5 уравнение не имеет смысла). А если бы нам нужно было решить это уравнение, то какой способ решения вы смогли бы предложить? (возведение обеих частей в квадрат).

х-6 = 4-х 2х = 10 х = 5.

Итак, единственный способ решения приводит к корню, который является посторонним. Возникает внешнее несоответствие между фактами приводит к проблемной ситуации.

Пример 3. Тема «Перпендикулярность плоскостей».

Учитель начинает урок не с объявления его темы, а с беседы о реальной ситуации, в которой невозможно верно решить вопрос и привлечения математики. Учитель напоминает о кладке стен, которую школьники наблюдали не раз. Вертикальность стен является правилом строителей. Правда, имеется несколько зданий, построенных с нарушением этого условия (наклонные башни в Ницце, шаровой дом в Дрездене), но известно что, с какими трудностями было связано их возведение и какие меры приходится принимать, чтобы эти сооружения не рухнули. Как же осуществляют строители контроль за вертикальностью стен? Выясняется, что для этого используют отвес. Естественно возникает вопрос: правильно ли поступают строители, является ли такая проверка достаточной? Проблема сформулирована, но пока класс ответить на поставленный вопрос не может. Несколько позже, рассмотрев одно из свойств перпендикулярных плоскостей, учащиеся смогут это сделать и только теперь объявляется тема урока. После доказательства теорем о перпендикулярных плоскостях учащиеся возвращаются к выдвинутой проблеме.

Свежие документы: Урок математики в 6 классе По теме «Решение уравнений»

III. Побуждение учащихся к сравнению, сопоставлению и противопоставлению фактов, явлений, правил, действий, в результате которых возникает проблемная ситуация.

Пример 1. 10 класс: тема «Возрастание и убывание функций». До объявления темы урока предложить учащимся решение двух уравнений:

х³= 27 х² = 9

х³=3³ х²= 3²

х = 3 х = 3

Уравнения решены одним и тем же способом и относятся к одному классу. Верно ли решены уравнении? (Второе уравнение решено неверно, кроме корня 3 имеет еще корень х = -3). У учащихся возникает вопрос почему? Решая эти уравнения мы выяснили при каких значениях аргумента х функция х³ принимает значение 27, а функция х² – значение 9? Результаты получились различные. В чем же дело? Очевидно дело в функциях х³ и х². Вероятно, что между функциями и х², которые относятся к одному классу функций существует весьма существенное различие? Для его отыскания ученикам предлагается начертить схематически графики функций и выяснить сколько раз функция х³ может принимать значение равное 27, а х² – значение 9? После этого ученики легко видят, что каждое свое значение х³ принимает только один раз, что нельзя сказать о функции х². Вспоминают как называются такие функции. Затем сообщается тема урока и идет работа над определениями возрастающей и убывающей функций.

Пример 2. Тема «Два перпендикуляра к плоскости». До сообщения темы урока учащиеся повторяют признаки параллельности прямых на плоскости, делают схематические рисунки. Затем с помощью моделей убеждаются, что второй признак параллельности прямых на плоскости в пространстве оказывается ложным высказыванием, то есть зависимости между параллельностью и перпендикулярностью прямых, которая существует на плоскости, в пространстве не существует.

Тогда возникает вопрос: «Какова же зависимость между параллельностью и перпендикулярностью в пространстве?»

С помощью моделей учащиеся выдвигают соответствующие гипотезы.

Пример 3. 10 класс: тема: «Взаимное расположение двух плоскостей. Признак параллельности плоскостей».

После рассмотрения взаимного расположения двух плоскостей и введение учащимся определения параллельных плоскостей по аналогии с определением параллельных прямых им предлагается выполнить упражнение: «Верно ли утверждение, что плоскости параллельны, если а) прямая лежащая в одной плоскости, параллельна прямой другой плоскости? Б) две прямые, лежащие в одной плоскости, соответственно параллельно двум прямым другой плоскости?» Возникает вопрос при каком же условии две плоскости параллельны? Учащиеся сами формулируют проблему и после сопоставления фактов выдвигают гипотезу об условии параллельности плоскостей.

IV. Решение нешаблонных задач. Прежде всего, следует отметить, что нередко смешивают нешаблонные задачи с трудными. Эти понятия не адекватны. Задача оказывается трудной, если учащиеся недостаточно подготовлены к ее решению (не знают некоторых формул, теорем, не знакомы с некоторыми приемами работы, для решения нужно использовать весьма удаленные факты). Проблемную ситуацию создают не трудные, а нешаблонные задачи. В уже рассмотренных, хотя в нем на первый взгляд ничего необычного нет. Примерами их могут быть, в частности, задачи логического содержания. Весьма эффективно использование связок задач. В каждой связке по 3-5 задач, первые достаточно просты, но работа над ними готовит к решению последней, которая содержит проблему.

Пример 1.

Доказать, что треугольник можно разрезать на три трапеции

A C

Можно ли разрезать прямоугольный треугольник на трапеции, среди которых нет прямоугольных? (сначала разрезать прямоугольный треугольник на два косоугольных)
Можно ли разрезать квадрат на трапеции, среди которых нет ни одной прямоугольной? (свести к предыдущей).
Какое наименьшее число трапеций может получиться при решении предыдущей задачи? (R = 8)

2 1

7 6

Проблемы, которые учитель может ставить перед учениками, обычно разрешаются на протяжении одного или нескольких уроков.

— «Почему треугольник назван «треугольником»? можно ли дать ему другое название, также связанное с его свойствами?»

— «Как можно объяснить название «развернутый угол»?»

Наиболее часто учителя создают проблемную ситуацию при помощи эксперимента, т.е. исследования частного случая.

Легко организовать проблемную ситуацию, предложив ученикам задачу, для решения которой нужны новые знания. Полезно при поддержать накал активности цепью проблемных вопросов, сменяющих один другой.

Пример 2.

Перед изучением теоремы Пифагора рассматривается практическая задача, для решения которой нужно уметь вычислять длину гипотенузы по длинам катетов.
Построение убеждает, что определенная зависимость между катетами и гипотенузой существует, ибо два катета определяют треугольник, в котором гипотенуза не может быть произвольной. Теперь возникает вопрос: «Можно ли выразить формулой зависимость между длинами катетов и гипотенузой?»

В поисках ответа рассматриваем удобный частный случай: прямоугольный треугольник с острыми углами по 45°. Получаем для него формулу c² = a² + b² и задаемся вопросом: «Верна ли формула для произвольного прямоугольного треугольника».

A B

b a

Дальнейшее исследование может быть построено по такой схеме. Поскольку в предлагаемую формулу входят величины a², b2, c², т.е. площадь квадратов со сторонами a, b и с, построим эти квадраты. Первое построение («пифагоровы штаммы») идею доказательства не поясняет. Тогда учитель предлагает связать величины a, b и с в комбинацию прямоугольных треугольников и квадратов, таким образом, как:

b B a

a b

C A

b a

a D b

Здесь площадь малого квадрата равна разности площади большого квадрата со стороной a+b и учетверенной площади прямоугольного треугольника со сторонами a, b и с т.е. c²= (a+b)²– 4 ab/2,

a² + b²+ 2 ab= a²+ b²

Можно ли считать формулу доказанной? Если исходить из такой фигуры, которая дана на чертеже, то да.

Рассмотрим, всегда ли можно для любого прямоугольного треугольника провести такое построение. Строим квадрат со стороной a+b и строим прямоугольные треугольники с катетами a и b. Выясняем, почему все такие треугольники равны. Остается показать, что фигура, образованная гипотенузами полученных прямоугольных треугольников является квадратом. Замечаем, что все стороны этой фигуры равны как гипотенуза равных треугольников. Но достаточно ли, этого чтобы фигура ABCD была квадратом? – Нет. Доказываем, что все углы этой фигуры прямые, так как они равны разности развернутого угла и острых углов данного прямоугольного треугольника. Следовательно, теорему Пифагора можно считать доказанной.

В качестве домашнего задания учитель может поручить ознакомиться с доказательством, данным в учебнике.

Но цепь вопросов, связанных с зависимостью сторон прямоугольного треугольника, может быть продолжена.

Спросим прежде всего: «Справедлива ли теорема Пифагора для непрямоугольного треугольника?» — Очевидно, нет, так как две стороны треугольника a и b не определяют однозначно его форму, а третья сторона меняет свою длину в зависимости от значения угла между сторонами a и b так, что a—b<c<a+b (при b<a)

Следующая проблема: «Верна ли теорема, обратная теореме Пифагора?»

Если квадрат большей стороны равен сумме квадратов двух других сторон, то треугольник прямоугольный, а именно: прямым является угол, лежащий против этой большей стороны. В самом деле, если бы это было не так и треугольник, стороны которого a и b и c связаны зависимостью

c²= a²+ b², оказался бы не прямоугольным, то стороны его не могли бы удовлетворять этому равенству.

Весьма полезно попросить учащихся указать ряд случаев применения теоремы Пифагора.

В поиске ответа на этот вопрос могут появиться такие задачи. Участок земли имеет форму прямоугольного треугольника. Наибольшая сторона участка выходит к реке и заболочена, если другие две стороны участка можно измерить непосредственно?

Длина часовой стрелки часов равна 6 мм., а минутной 8 мм. Сколько времени показывают часы, если расстояние между концами стрелок 10 мм., а минутная стоит на отметке «12»?

Интересный вопрос: «На чем основан способ построения прямого угла в «египетском» треугольнике со сторонами 3.4 и 5?»

Проблемная ситуация может быть создана не только при рассмотрении теоретического вопроса, но и при решении задач или какого-то практического упражнения.

Пример 3.

«В равностороннем треугольнике проведена высота. Какие свойства имеют образовавшиеся треугольники?»

Ученики устанавливают, что эти треугольники прямоугольные, равные, острые углы в них составляют 60° и 30°, и, наконец катет, противолежащий углу в 30°, равен половине гипотенузы. Учитель ставит вопрос: «Имеется ли какая-нибудь зависимость между значениями углов и длинами двух сторон треугольника?» Чертеж покажет, что если одна сторона треугольника в 2 раза больше другой, то необязательно, чтобы его углы составляли 30°, 60°, 90°. Зато если дан треугольник с углами в 30°, 60° и 90°, то катет, лежащий против угла в 30°, скорее всего, равен половине гипотенузы. Так приходим к свойству прямоугольного треугольника с углом в 30°.

Проблемные ситуации возникают также в случае необходимости проверить заключение, сделанное на основе интуиции, на основе аналогии или попытки обобщения.

Примеры учебных проблем:

Сумма внутренних углов треугольника равна 180°. Равна ли 180° сумма внутренних углов четырехугольника? Пятиугольника? Средняя линия треугольника параллельна основанию. Имеет ли такое же свойство средняя линия ромба? Параллелограмма? Четырехугольника?

В треугольнике биссектрисы пересекаются в одной точке. Можно ли то же самое сказать о биссектрисах углов четырехугольника? Можно ли применить формулу площади трапеции к вычислению площади параллелограмма? Прямоугольника? Ромба? Квадрата?

Пример 4.

Можно использовать домашние задания, которые позволяют выдвинуть на следующем уроке учебные проблемы, поставившие школьника дома в тупик. К примеру, перед изучением темы об одном замечательном свойстве окружности, ученики получают такое практическое задание на дом: «Дана прямая l и две точки А и В вне ее. С помощью угольника найти на прямой l такую точку С, чтобы угол АСВ был прямым». Предупреждаю о возможности нескольких решений и требую рассмотреть различные положения точек А,В и прямой l. Дома учащиеся, взяв в помощь угольник, сопоставят его стороны с точками А и В, а затем начнут вертеть угольник, пытаясь найти нужную точку на прямой. В зависимости от расположения точек А,В и прямой l, они ее либо найдут (возможны два решения) либо – нет.

При проверке домашнего задания (перед изучением новой темы), задаю вопрос классу: «Нельзя ли решить эту задачу с помощью циркуля и линейки?» Этот вопрос побуждает ребят проанализировать действия, совершенные при попытке решения задачи. И некоторым из них придет в голову мысль, что, сами того не зная, они пользовались свойством циркуля. А будут и такие, кто уже дома догадается использовать циркуль в работе. Далее учащиеся приступают к изучению новой темы, при этом новый материал может рассказать учитель, а лучше провести урок в форме беседы (с помощью системы вопросов и ответов). В конце урока дается возможность уже четко ответить на поставленный ранее вопрос.

Пример 5.

Проблемная ситуация возникнет, если предложить ученикам выполнить какое-то действие, на первый взгляд не вызывающее затруднения. Так, перед изучением темы о сумме внутренних углов треугольника можно предложить такую задачу: Построить треугольник по трем заданным углам:

∟А=90°, ∟B=60°, ∟С=45°;
∟А=70°, ∟B=30°, ∟С=50°;
∟А=50°, ∟B=60°, ∟С=70°.

Учащиеся, вооружившись линейкой и транспортиром, начинают

строить треугольники. В первом случае, построив углы А и В и отложив угол в 45° от луча АС (или ВС, кому как нравится), ребята увидят, что вместо треугольника получается четырехугольник. Во втором случае независимо от того, какие два первые угла школьники выбирают для построения, всегда получается треугольник по трем заданным углам. По окончании уже можно выдвинуть предположение о сумме внутренних углов треугольника. Здесь уместен провокационный вопрос: «В каком треугольнике, по вашему мнению, сумма внутренних углов больше, в остроугольном или тупоугольном?» Практика показывает, что в каждом классе найдутся несколько человек, которые, зная, что тупой угол всегда больше острого, по анальгии скажут, что сумма внутренних углов тупоугольного треугольника, больше, чем остроугольного.

Я предлагаю им на практике проверить свое утверждение.

Пример 6.

Когда учитель побуждает учащихся к сравнению, к сопоставлению и противопоставлению фактов, возникает познавательное затруднение. Так, перед изучением темы о формуле корней квадратного уравнения учитель может обратить внимание на примеры, решенные на предыдущем уроке и дома способом выделения квадрата двучлена, и предложить для сравнения решить следующие уравнения: х²+ 8х – 10 = 0

Ребята приступают к работе и выполняют задание так:

х² + 2 * 4х + 16 – 16 – 10 = 0

(х + 4)² – 26 = 0

Примеры типа ( х+а )² ± b = 0, где b не является квадратом целого числа, учащиеся еще не решали. И на этом этапе они обязательно споткнутся. После чего учитель объявляет, что известный ребятам способ решения квадратных уравнений выделения квадрата двучлена универсален, но требует каждый раз громоздких преобразований. Поэтому удобнее, решив квадратное уравнение в общем виде, вывести формулу его корней и в дальнейшем решать квадратные уравнения по этой формуле. Затем учитель объявляет новую тему урока, а ученики психологически готовы ее воспринять.

Пример 7. «Расширение множества рациональных чисел»

Повторение множеств чисел, изученных ранее N c Z c Q

S_кв = а², с другой стороны его можно составить из 4-х равных прямоугольных треугольников с катетом равным 1, то есть его S равна S двух квадратов со стороной 1. Тогда а² = 2*1, а² = 2.

) достроим треугольник до квадрата.

Вот длина этого отрезка, вот место этого числа на координатной прямой.
Далее учитель доказывает теорему, что не существует рационального числа, квадрат которого равен 2.

Возникает проблемная ситуация: среди изученных чисел этого числа не существует, но с другой стороны мы можем указать место точку на числовой прямой, которое ему соответствует, то есть, есть такие точки, которые соответствуют каким-то числам, которых нет среди рациональных. Значит, есть числа, которых мы еще не знаем.

Пример 8. «Нахождение дроби от числа».

Решим задачу: «Огород занимает 6 га земляного участка. На 2/3 огорода посажен картофель. Какую часть всего земляного участка занимает картофель?» Можем ли мы решить задачу? Как?

6/3*2 = 4 (га)

Охарактеризуйте задачу. Отойдем от огорода и картофеля, перейдем к величинам. Что нам известно? [целое]. Что нужно найти? [часть]
Возьмем ту же задачу, но изменим значения одной величины: «Огород занимает 4/5 земельного участка. На 2/3 огорода посажен картофель. Какую часть всего земельного участка занимает картофель?» Изменился ли математический смысл задачи? [нет]. Значит, опять известно целое, а ищем часть. Влияет ли замена 6 на 4/5 на решение? Можно ли решить? [нет].
Что за ситуацию мы получили?

[Обе задачи на нахождение части от числа. Но одну мы можем решить зная определенные дроби, понятие числителя и знаменателя, а вторую не можем]. Проблема: не знаем общего правила нахождения дроби от числа. Нужно вывести это правило.

Пример 9. Свойства уравнений.

Уравнения на доске записаны вперемешку и без номеров.

х+20=8 5х=2х+6

5-х=11 3х+8=5х-2

-1/4х=-3

4х/10=-2

-8/х=5

1) Вопрос учащимся: на какие две группы можно разбить эти семь уравнений? Что это за группы? Чем они отличаются? Ученики разбивают на 1-5, 6-7. (В I группе неизвестное х только в левой части, их мы можем решить, а во II – в обеих частях стоит х, не можем решить).

2) Какие правила нужно знать, чтобы решить уравнения I группы?

— найти неизвестное слагаемой;

— неизвестный множитель;

— неизвестный делитель;

— неизвестное вычитаемое;

— неизвестное делимое.

5 уравнений – 5 правил.

А почему не можем решить уравнения II группы?

3) Работая в 4-ках методом «мозгового штурма» обсудить проблемы, которые можно поставить для каждой группы уравнений.

4) Выводы учащихся: Для I группы – для каждого вида уравнений свое правило – их много. Попытаться уменьшить количество правил. Для II группы – сделать уравнения похожими на уравнения I группы, то есть чтобы неизвестное было только в левой части.

Итог: уменьшить количество правил и научиться переносить слагаемые из одной части в другую. Для этого нужно изучить части уравнений.

Анализ результатов деятельности позволяет сделать вывод, что в классах, где последовательно и целенаправленно осуществляется работа по развитию умений и навыков самостоятельной деятельности, ученики самостоятельно совершенствуют свои знания, качество знаний достаточно высокое. Так, рост динамики индивидуальных результатов обученности в 2012 году по сравнению с 2011 годом повысился в 9-х классах на 8%, в профильном десятом инфомационно-технологическом классе – на 46%. Количество обучающихя на 4 и 5 по предмету за три года увеличилось на 9% и составляет на конец 2011-2012 учебного года 64%. Имеется рост качества результатов сдачи ГИА по математике в новой форме с 75% до 79% .

Эффективность технологии проблемного обучения на уроках математики можно проследить по результатам диагностических контрольных работ по математике в формате ЕГЭ. Если с ДКР № 1 справился 71% одиннадцатиклассников, то с работой № 2 справились уже 96% выпускников.

Возросло количество учащихся, проявляющих интерес к предмету. Ежегодно в ОУ проводится школьный этап Международного конкурса «Кенгуру». Охват учащихся составляет 60% от общего числа учащихся 5-11 классов.

Таким образом, можно сделать вывод, опираясь на проведенную мною работу, что в целом проблемное обучение оказывает влияние на более качественное усвоение знаний, на воспитание учебной мотивации, развитие мыслительных операций.

Список литературы

Бакланский О.Е. Проблемное обучение: обоснование и реализация // Наука и школа. – 2000. — № 1
Вилькеев Д.В. Методы научного познания в школьном обучении. – К., 2008
Гнеденко Б.В. О развитии мышления и речи на уроках математики // математика в школе. – 2006. — № 3
Занков Л.В.Дидактика и жизнь. – М., 1999
Карелина Т.М. О проблемных ситуациях на уроках геометрии // Математика в школе. – 2010. — № 5
Карелина Т.М. Методы проблемного обучения // Математика в школе. – 2009. — № 5
Крутецкий В.А. Основы педагогической психологии. – М., 1972.
Максимова В.Н. Проблемный подход к обучению в школе. Методическое пособие по спецкурсу. – Л., 2001.
Матюшкин А.М. Проблемные ситуации в мышлении и обучении. – М., 2002.
Махмутов М.И. Организация проблемного обучения. – М., 2007.
Махмутов М.И. Проблемное обучение (основные вопросы теории).- М.,2005
Селевко Г.К. Современные образовательные технологии. – М., 2008.