Муниципальное казённое общеобразовательное учреждение
«Дедиловская средняя общеобразовательная школа» администрации муниципального образования
cosα
sinα
Конспект урока по теме:
«Значения синуса, косинуса и тангенса
некоторых углов»
cosβ tgβ


Тема урока: «Значения синуса, косинуса и тангенса
некоторых углов».
Тип урока: изучение нового материала
Формы организации деятельности на уроке: эвристическая беседа, самостоятельная работа.
Методы и методические приемы: дифференцированный, частично-поисковый, исследовательский.
Цель урока:
— закрепление знаний по теме «Синус, косинус и тангенса острого угла», изучение и первичное закрепление новых знаний по теме урока, вызвать интерес через создание проблемной ситуации.
Задачи урока:
Образовательная:
— повторение ранее изученного материала;
— овладение знаниями и умениями, необходимыми для применения в практической деятельности, изучения смежных дисциплин.
Развивающая:
— развитие памяти, речи, любознательности, познавательного интереса;
— развитие творческой самостоятельности мышления учащихся;
— развитие умственных операций (прием создания образа, перенос знаний, обобщение, сравнение, анализ, синтез);
— развитие вычислительных навыков;
— развитие общеучебных умений и навыков.
Воспитательная:
— воспитание аккуратности, дисциплины;
— воспитание настойчивости в достижении цели;
— воспитание внимания, самоконтроля, интереса к предмету.
Оборудование:
Компьютер.
Интерактивная доска
Презентация Microsoft Power Point.
Ход урока:
1. Организационный момент.
Приветствие.
Определение отсутствующих. Проверка готовности учащихся к уроку.
Организация внимания учащихся, настроить учащихся на позитивное восприятие изучаемого материала.
Слайд 1. Сообщение темы урока «Значение синуса, косинуса и тангенса некоторых углов». Учащиеся записывают тему урока в тетрадях.
Начать наш урок хочется со слов венгерского математика Дьёрда Пойа «Лучший способ изучить что либо – это открыть самому» Слайд 2. В основу урока положим китайскую мудрость. Слайд 3.
«Ты можешь стать умнее тремя путями: путем опыта – это самый горький путь, путем подражания – это самый легкий путь, путем размышления – это самый благородный путь».
Сегодня на уроке: проводим свои исследования, делаем открытие, не боимся ошибаться, ибо любая мысль есть продолжение поиска и нашего совершенства. Слайд 4.
На доске чертеж прямоугольного треугольника АВС. Слайд 5.
Опрос учащихся.
Сформулируйте теорему Пифагора. Учащиеся отвечают: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». Запишите на доске теорему Пифагора для данного прямоугольного треугольника АВС. Учащийся выходит к доске и записывает выражение 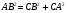 .
.
Дайте определение косинуса острого угла. Учащиеся отвечают: «В прямоугольном треугольнике косинусом острого угла называется отношение прилежащего катета к гипотенузе». Запишите на доске косинусы острых углов данного треугольника. Учащийся выходик к доске и записывает 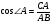 ,
, 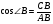 .
.
Дайте определение синуса острого угла. Учащиеся отвечают: «В прямоугольном треугольнике синусом острого угла называется отношение противолежащего катета к гипотенузе». Запишите на доске синусы острых углов данного треугольника. Учащийся на доске записывает 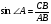 ,
, 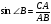 .
.
Дайте определение тангенса острого угла. Учащиеся отвечают: «В прямоугольном треугольнике отношение противолежащего катету к прилежащему называется тангенсом острого угла». Запишите на доске тангенсы острых углов данного треугольника. Учащийся на доске записывает 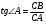 ,
, 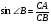 .
.
2. Изучение нового материала.
Мы с вами повторили теорему Пифагора и основные тригонометрические понятия. Эти знания вам пригодятся для изучения новой теоремы. Для начала вспомним теорему о сумме углов треугольника. Учащиеся отвечают: «В любом треугольнике сумма углов равна 180°.
Так как треугольник АВС прямоугольный с прямым углом С, пусть 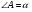 , тогда
, тогда 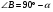 . Запишите значения косинуса и синуса для полученных углов. Учащийся выходит к доске и записывает
. Запишите значения косинуса и синуса для полученных углов. Учащийся выходит к доске и записывает 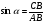 ,
,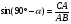 ,
,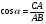 ,
, 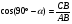 . Обратите внимание на записи. Что вы увидели? Учащиеся отвечают, что
. Обратите внимание на записи. Что вы увидели? Учащиеся отвечают, что 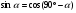 и
и 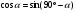 . Это и есть теорема, которая лежит в основе нашего урока, вы ее вывели сами. Запишем теорему в тетрадях. Учащиеся записывают теорему «Для любого острого угла α
. Это и есть теорема, которая лежит в основе нашего урока, вы ее вывели сами. Запишем теорему в тетрадях. Учащиеся записывают теорему «Для любого острого угла α 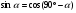 ,
, 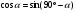 ».
».
А зачем же мы вообще изучаем тригонометрические функции? Я вам говорила на первых уроках, что они пригодятся в дальнейшем при нахождении площадей геометрических фигур и при изучении математического анализа при решении тригонометрических уравнений и неравенств. А откуда в математику они пришли? Об этом расскажут в своих сообщениях Шахов Семен и Агуреев Илья. Доклады учащихся.
Вы научились пользоваться таблицей Брадиса для нахождения градусной меры острого угла, но не всегда она есть под рукой. А в математике часто встречаются значения углов 30, 45 и 60 градусов для решения задач. И следующим заданием для вас будет – найти эти значения. Слайд 6.
Найдем синус, косинус и тангенс угла 45°. Построим прямоугольный треугольник с острым углом 45°. Чему будет равен второй угол? Тоже 45°, поэтому треугольник равнобедренный. Пусть катеты треугольника равны а. Что нам неизвестно в данном треугольнике? Гипотенуза. Найдем ее по теореме Пифагора. Учащиеся самостоятельно находят гипотенузу. Один работает у доски. 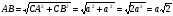 .
.
Вычисляем 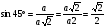 ,
,
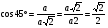 ,
,
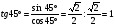
Найдем синус, косинус и тангенс угла 30°. Слайд 7. Для этого построим равносторонний треугольник АВС со стороной а. Из вершины А опустим перпендикуляр. Вспомните, чем является в равнобедренном треугольнике высота? Учащиеся отвечают: «В равнобедренном треугольнике медиана является и высотой и биссектрисой». А что из этого следует? Что угол А, равный 60° , поделится пополам, то есть на 30° — то, что и требуется. Следовательно сторона а разобьется на 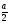 . Неизвестна высота АD. С помощью какой теоремы можно ее вычислить? Учащиеся записывают в тетрадях теорему Пифагора для треугольника ACD.
. Неизвестна высота АD. С помощью какой теоремы можно ее вычислить? Учащиеся записывают в тетрадях теорему Пифагора для треугольника ACD. 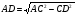 . Подставим в эту формулу известные данные, то есть
. Подставим в эту формулу известные данные, то есть 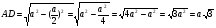 ,
,
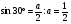 ,
,
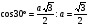 ,
,

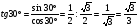 .
.
По изученной сегодня теореме найдем синус и косинус 60°.
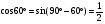 ,
, 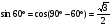 .
.
Остается вычислить тангенс 60°. 
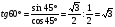 .
.
А как же запомнить эти значения? Слайд 8. Объяснение как с помощью руки можно запомнить значения тригонометрических функций. Слайд 9.
3. Практическая часть.
Открыли учебник на странице 99 и нашли № 66. Данную задачу учащиеся решают самостоятельно.
Задача «В прямоугольном треугольнике с гипотенузой а и углом 60° найдите катет, противолежащий этому углу».
Решение: так как необходимо найти противолежащий катет, то воспользуемся для его нахождения синусом 60°. 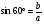 ,
, 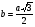 .
.
Ответ: 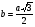 .
.
Итог урока: Слайд 11. Пусть наши достижения не будут такими крупными, как достижения великих ученых, но ведь это наши, собственные открытия!
Домашнее задание: учить пункт 69, № 67,71( с пояснением).
Самоанализ урока
Учитель математики: Соловьева Надежда Юрьевна.
Класс: 8.
Тип урока: изучение нового материала
Формы организации деятельности на уроке: эвристическая беседа, самостоятельная работа.
Методы и методические приемы: дифференцированный, частично-поисковый, исследовательский.
Оборудование: Презентация Microsoft Power Point, созданная лично учителем.
Целью урока я ставила закрепление знаний по теме «Синус, косинус и тангенс острого угла», изучение и первичное закрепление новых знаний по теме урока, вызвать интерес через создание проблемной ситуации.
Характеристика класса: по успеваемости класс ниже среднего, из 16 обучающихся по моему предмету имеют оценку «4» — четыре человека, остальные — «3». Уровень познавательной деятельности также низкий.
Урок проходил в рамках школьной методической недели. Основным направлением являлась исследовательская деятельность и работа с особо успевающими детьми.
Урок начался с приветствия учащихся, настроила их на положительное восприятие изучаемой темы.
Перед изучением нового материала с учащимися повторили теорему Пифагору и основные тригонометрические понятия, которые необходимы для урока. Дети довольно активно отвечали на поставленные вопросы, Разоренов Вячеслав записал на доске теорему Пифагора для треугольника, который был изображен на доске, Тюндин Кирилл – соотношения сторон треугольника для синуса, косинуса и тангенса острых углов. Далее с помощью наводящих вопросов, ученики вывели теорему по новому материалу. Затем Агуреев Илья и Шахов Семен рассказали о появление тригонометрических функций в математике и «Тригонометрия в жизни». После сообщений я вновь поставила проблему, а что делать, если у нас под рукой нет таблицы Брадиса, но нам необходимо узнать значение угла? Сказала, что очень часто приходится иметь дело с синусами, косинусами и тангенсами 30,45 и 60 градусов. Моргунов Даниил, который является одним из успевающим учеником, вычислил значения синуса, косинуса 45, 30 и 60 градусов. Но как было ранее сказано, что класс мало отличается активной познавательной деятельности и в работе на уроках, то вычисления, на мой взгляд, проходили несколько медленнее, как хотелось. Остальные дети ждали, когда будет на доске записано решение, самостоятельно приступили к решение несколько человек.
Запланированную задачу решить не успели. Но ее я им задала в качестве домашнего задания. Но считаю, что в ходе работе ученики достаточно хорошо усвоили и повторили то, что они изучали ранее.
Цели урока были решены. Главной целью было сформировать заинтересованность учащихся и формирование позитивных мотивов к изучению математики, поскольку у учащихся большие пробелы в фактических знаниях и умениях, пробелы в навыках учебного труда. А при отсутствии заинтересованности учащихся и позитивных мотивах к изучению математики, ликвидировать эти пробелы невозможно.
Стиль отношений с учащимися активно-положительный. Ученики на уроке работали практически все. Во всех этапах урока ярко проявлялось обращение к ранее накопившимся знаниям и умениям учеников. Исследовательская деятельность учащихся на уроке – одно из обязательных условий урока для достижения целей урока.
Самостоятельная работа не может быть вполне успешной, если ученик не может правильно оценить свои возможности, проконтролировать себя. Исследовательская работа, организованная на уроке, приучает учащихся не только к контролю со стороны учителя (как это обычно бывает), но и к самоконтролю, самоанализу своей деятельности, помогает планировать свою работу самостоятельно, а не по подсказке учителя. Во время урока учащимся предоставлялось максимум самостоятельности. Но это не означает, что я на этом уроке ничего не делала. В ходе урока присутствовало наводяще — диалогическое общение. В учебном процессе приветствуется свободное выражение учениками своего мнения без опасения критики. Со стороны учителя проявлялась доброжелательность, уравновешенность.
Можно сделать вывод, что данная форма урока позволяет организовать равноправное общение, создать благоприятный психологический климат и атмосферу сотрудничества.
