1. Повторение основных понятий, связанных с прямоугольным треугольником
На этом уроке мы познакомимся с синусом, косинусом и тангенсом – тригонометрическими функциями, связывающими острый угол прямоугольного треугольника с катетами и гипотенузой этого треугольника. Это очень важные понятия, которые будут встречаться не только в геометрии, но и в алгебре, физике и во многих других науках.
Напомним основные сведения о прямоугольном треугольнике (см. Рис. 1).
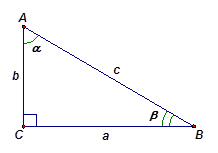
Рис. 1
![]() ;
;
![]() – катеты;
– катеты; ![]() – гипотенуза.
– гипотенуза.
Также в прямоугольном треугольнике сумма острых углов равна ![]() :
: ![]() .
.
Для прямоугольного треугольника также верна теорема Пифагора: ![]() .
.
Введём теперь понятие синуса, косинуса и тангенса острого угла прямоугольного треугольника.
2. Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника
Определение
Синусом острого угла прямоугольного треугольника называется отношение противолежащего этому углу катета к гипотенузе.
![]() ,
, ![]() .
.
Определение
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к гипотенузе.
![]() ,
, ![]() .
.
Определение
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего этому углу катета к прилежащему катету.
![]() ,
, ![]() .
.
3. Связь катетов и гипотенузы, двух катетов через тригонометрические функции угла
С помощью введённых понятий можно находить катеты или гипотенузу.
Например, из формулы: ![]() . Аналогично:
. Аналогично: ![]() .
.
Также можно получить формулу для связи длин двух катетов: ![]() .
.
4. Связь синуса и косинуса двух острых углов прямоугольного треугольника
При решении задач очень важно знать соотношения между синусом, косинусом и тангенсом острого угла прямоугольного треугольника.
Рассмотрим следующие две формулы: 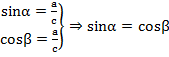 . Так как сумма острых углов прямоугольного треугольника равна
. Так как сумма острых углов прямоугольного треугольника равна ![]() , то формула приобретает следующий вид:
, то формула приобретает следующий вид:
![]()
Аналогично получаем: 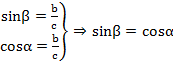 . Так как сумма острых углов прямоугольного треугольника равна
. Так как сумма острых углов прямоугольного треугольника равна ![]() , то формула приобретает следующий вид:
, то формула приобретает следующий вид:
![]()
5. Формула, связывающая тангенс с синусом и косинусом
Докажем теперь важную формулу, связывающую тангенс с синусом и косинусом:
![]()
6. Доказательство независимости значения тригонометрических функций от размеров треугольника
Доказательство
Запишем определение синуса и косинуса острого угла прямоугольного треугольника: ![]() ,
, ![]() . Тогда:
. Тогда: ![]() . Доказано.
. Доказано.
Аналогично: ![]() .
.
Рассмотрим следующую важную задачу.
Задача
Даны прямоугольные треугольники ![]() . Кроме того,
. Кроме того, ![]() .
.
Доказать:![]() .
.
Доказательство
![]() (так как оба треугольника прямоугольные с равными острыми углами). Значит, выполняется следующее соотношение:
(так как оба треугольника прямоугольные с равными острыми углами). Значит, выполняется следующее соотношение: ![]() .
.
Отсюда получаем: ![]() .
.
![]() .
.
![]() .
.
Доказано.
Вывод: синус, косинус и тангенс не зависят от треугольника, а зависят только от угла.
7. Основное тригонометрическое тождество
Сформулируем и докажем одну из важнейших теорем, связывающих синус и косинус острого угла прямоугольного треугольника, – основное тригонометрическое тождество.
Основное тригонометрическое тождество: ![]() .
.
Примечание: ![]()
Доказательство
![]() , тогда:
, тогда: ![]() (при доказательстве мы пользовались теоремой Пифагора:
(при доказательстве мы пользовались теоремой Пифагора: ![]() ).
).
Доказано.
Рассмотрим пример, иллюстрирующий связь тригонометрических функций.
Дано: ![]() – прямоугольный (
– прямоугольный (![]() ),
), ![]() .
.
Найти: ![]()
Решение
Воспользуемся основным тригонометрическим тождеством: ![]() . Подставим в него известное нам значение синуса:
. Подставим в него известное нам значение синуса: ![]() . Отсюда:
. Отсюда: ![]() . Так как косинус, по определению, – это отношение катета к гипотенузе, то он может быть только положительным, поэтому:
. Так как косинус, по определению, – это отношение катета к гипотенузе, то он может быть только положительным, поэтому: ![]() .
.
Найдём теперь тангенс угла, пользуясь формулой: ![]() .
.
Ответ: ![]() .
.
На этом уроке мы рассмотрели понятия синуса, косинуса и тангенса острого угла прямоугольного треугольника, вывели некоторые их свойства и формулы связи между этими величинами. На следующем уроке мы познакомимся со значениями синуса, косинуса и тангенса для некоторых конкретных значений углов.
