Конспект урока по Алгебра «СБОРНИК АЛГОРИТМОВ» 9 класс

Т.Г.Ефименко

учитель математики

Муниципального бюджетного образовательного

учреждения Белоярского района

«Общеобразовательная средняя (полная) школа № 1 г.Белоярский»

Ханты-Мансийского автономного округа-Югры

Тюменской области

СБОРНИК АЛГОРИТМОВ

ПОСОБИЕ ПО АЛГЕБРЕ

ДЛЯ УЧАЩИХСЯ 9 КЛАССОВ

Предисловие

Данное пособие предназначено для учащихся 9-х классов общеобразовательных школ, занимающихся по учебнику «Алгебра 9» под редакцией С.А.Теляковского. Однако, его легко можно адаптировать для преподавания по учебнику других авторов.

Нередко на уроках слышишь от учеников фразу «А с чего начать?». Разобранные примеры в учебнике не могут в достаточной мере помочь таким учащимся. Они испытывают затруднения в определении последовательности выполняемых действий.

Целью сборника является оказание помощи ученикам, испытывающим затруднения в выполнении заданий по алгебре.

Пособие можно адаптировать к учебникам других авторов, а также к выполнению заданий по другим предметам — геометрии, физике, химии.

В сборнике имеются не только алгоритмы по определенной теме учебного курса, но и некоторые основные понятия. Кроме того, рассмотрены примеры на применение алгоритмов по каждой теме.

Надеюсь, данное пособие поможет выпускникам 9-х классов в подготовке к итоговой государственной аттестации.

I. Тема «ФУНКЦИИ И ИХ СВОЙСТВА»

1. Функция — такая зависимость переменной х от переменной у, при которой каждому значению переменной х соответствует единственное значение переменной у (х — независимая переменная или аргумент, у — зависимая переменная или функция).

2. Область определения функции D(f) — все значения независимой переменной х (аргумента), т.е. те, при которых функция имеет смысл.

3. Область значения функции Е(f) — все значения зависимой переменной у.

4. Свойства функции:

• нули функции (значения х, при которых у = 0);

• возрастание (убывание);

• четность (симметрия относительно ОУ), нечетность (симметрия относительно начала координат или т.О);

• промежутки знакопостоянства;

• наибольшее (наименьшее) значение.

Алгоритм 1

Чтобы найти область определения функции, надо:

1. Внимательно посмотреть на формулу, которой задана функция.

2. Если формула, которой задана функция, представляет собой целое выражение, а также нет корня, то областью определения функции является вся числовая прямая, т.е. х  (−∞; + ∞) или множество R.

3. Если в знаменателе дроби имеется переменная (дробное выражение), то надо знаменатель приравнять к нулю и решить получившееся уравнение. Найденные значения переменной необходимо исключить из множества значений аргумента.

4. Если в формуле имеется квадратный корень в числителе, то надо составить и решить неравенство, в котором левая часть — подкоренное выражение, правая часть  0.

5. Если в формуле имеется квадратный корень в знаменателе, то надо составить и решить неравенство, в котором левая часть — подкоренное выражение, правая часть  0.

6. Записать полученный ответ в виде множества.

Пример. Найти область определения функции, заданной формулой:

а) у = 5х + 9; б) ; в) .

Решение:

а) у = 5х + 9.

Правая часть формулы является целым выражением, следовательно, областью определения функции является вся числовая прямая (п.2 алгоритма). Ответ: D(f) = R.

б)

В правой части формулы имеется переменная в знаменателе дроби. Приравниваем это выражение к нулю и решаем полученное уравнение.

2х + 3 = 0, 2х = -3, х = -1,5.

Найденное значение х из ответа надо исключить.

(Можно для себя записывать так: 2х + 3 ≠ 0, х ≠ -1,5.)

Ответ: х ≠ -1,5 или х  (−∞: — 1,5)  (- 1,5; + ∞).

в) .

Зная, что подкоренное выражение может быть неотрицательным (положительным или равным нулю), решаем неравенство

2х — 5  0, 2х  5, х  2,5.

Ответ: х  [2,5; + ∞).

II. Тема «КВАДРАТНЫЙ ТРЕХЧЛЕН»

1. Квадратный трехчлен — многочлен вида ах² + bх + с, где х — переменная, а, b, с — числа, причем а ≠ 0.

2. Корень квадратного трехчлена — значение переменной, при котором его значение равно нулю.

Алгоритм 2

Чтобы выяснить, имеет ли квадратный трехчлен корни или их число, надо:

1. приравнять квадратный трехчлен к нулю;

2. определить тип получившегося квадратного уравнения;

3. уравнение типа ах² + bх = 0 всегда имеет два корня;

4. уравнение типа ах² + с = 0 имеет два корня х_1,2 = ± , если  0 и не имеет корней, если < 0;

5. уравнение типа ах² + bх + с = 0 имеет два различных корня, если D  0, имеет один корень (два одинаковых корня), если D = 0 и не имеет корней, если D < 0.

Алгоритм 3

Чтобы найти корень (корни) квадратного трехчлена, надо:

1. приравнять квадратный трехчлен к нулю;

2. определить вид квадратного уравнения — полное или неполное;

3. неполное квадратное уравнение решить вынесением общего множителя за скобки или выражением переменной;

4. решить полное квадратное уравнение, используя формулы

D = b² — 4ас, х_1,2 = ;

Пример. Найти корни квадратного трехчлена:

а) х² + х — 6; б) 12х² — 12; в) — 0,3х² + 1,5х.

Решение:

а) х² + х — 6 = 0.

D = 1² — 4 · 1 · (- 6) = 1 + 24 = 25  0, 2 корня;

х₁ = ; х₂ = .

Ответ: х = -3; 2.

б) 12х² — 12 = 0,

12 (х² — 1) = 0,

х² — 1 = 0,

х² = 1,

х_1,2 = ± 1. Ответ: х_1,2 = ± 1.

в) — 0,3х² + 1,5х = 0,

— 0,3х (х — 5) = 0,

х₁ = 0 или х — 5 = 0,

х₂ = 5. Ответ: х₁ = 0; х₂ = 5.

Алгоритм 4

Чтобы разложить квадратный трехчлен на множители по формуле ах² + bх + с = а (х – х₁)(х – х₂), надо:

1. найти корни квадратного трехчлена (см. алгоритм 3);

2. подставить значения х₁ и х₂ в формулу.

III. Тема «КВАДРАТИЧНАЯ ФУНКЦИЯ»

1. Квадратичная функция (парабола) — функция вида у = ах² + bх + с, где х и у — переменные, а, b, с — числа, а ≠ 0.

2. Областью определения квадратичной функции является множество всех действительных чисел, т.е. х  (−∞; + ∞).

3. Графиком функции у = ах² + bх + с является парабола.

4. Расположение параболы в системе координат:

1) у = ах² — график симметричен относительно оси у, вершина графика совпадает с началом координат; при а  0 ветви параболы направлены вверх, при а < 0 ветви вниз;

2) у = а(х — m)² — может быть получен путем смещения графика у = ах² по оси х: вправо на т единиц при т  0 и влево на т единиц при т < 0;

3) у = ах² + n — может быть получен путем смещения графика у = ах² по оси у: вверх на п единиц при п  0 и вниз на п единиц при п < 0;

4) у = а(х — m)² + n — совмещение преобразований графика п.2) и 3);

5) у = ах² + вх + с, можно получить формулу вида у = а(х — m)² + n путем выделения квадрата двучлена или пользоваться алгоритмом.

Алгоритм 5

Чтобы построить график квадратичной функции вида у = ах² + вх + с, надо:

1. выяснить направление ветвей параболы;

2. найти координаты вершины параболы (т; п), где т = и п = ат² + вт + с или , и отметить ее в координатной плоскости;

3. дополнительно можно решить уравнение ах² + вх + с = 0 для нахождения точек х₁ и х₂ пересечения графика с осью х;

4. составить таблицу значений (ориентировочно 7 значений х), где (т; п) занимает центральное место, остальные значения х симметричны относительно т,

5. построить точки, координаты которых вычислены в таблице;

6. соединить полученные точки плавной линией;

7. подписать график параболы.

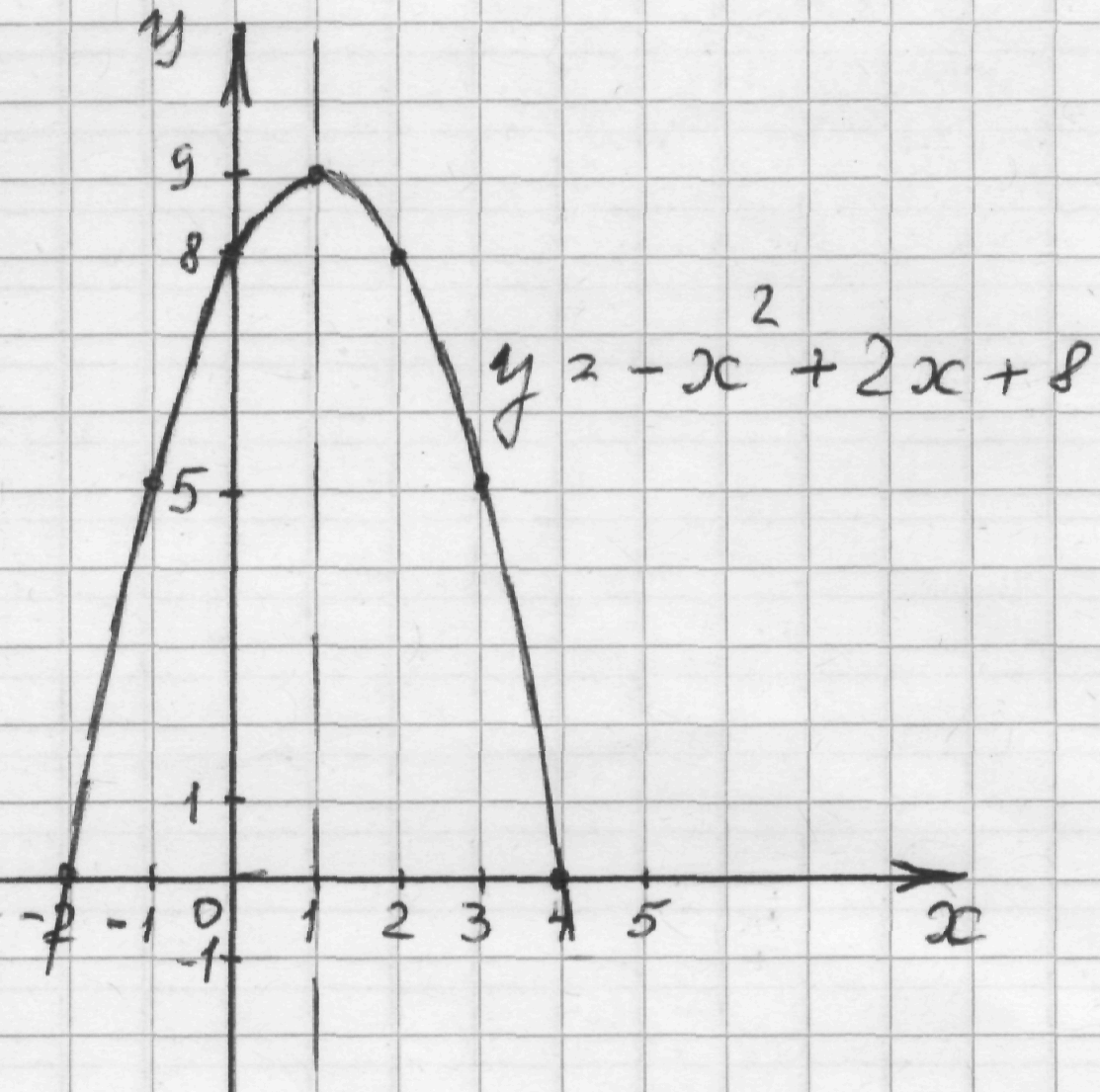
Пример. Построить график функции у = – х² + 2х + 8.

1. Графиком функции является парабола, ветви которой направлены вниз, т.к. а < 0.

2. Найдем координаты вершины параболы (т; п): т = , п = – 1² + 2 · 1 + 8 = 9, (1; 9).

3. Решим уравнение – х² + 2х + 8 = 0. D = 4 +32 = 36, х₁ = 4, х₂ = — 2

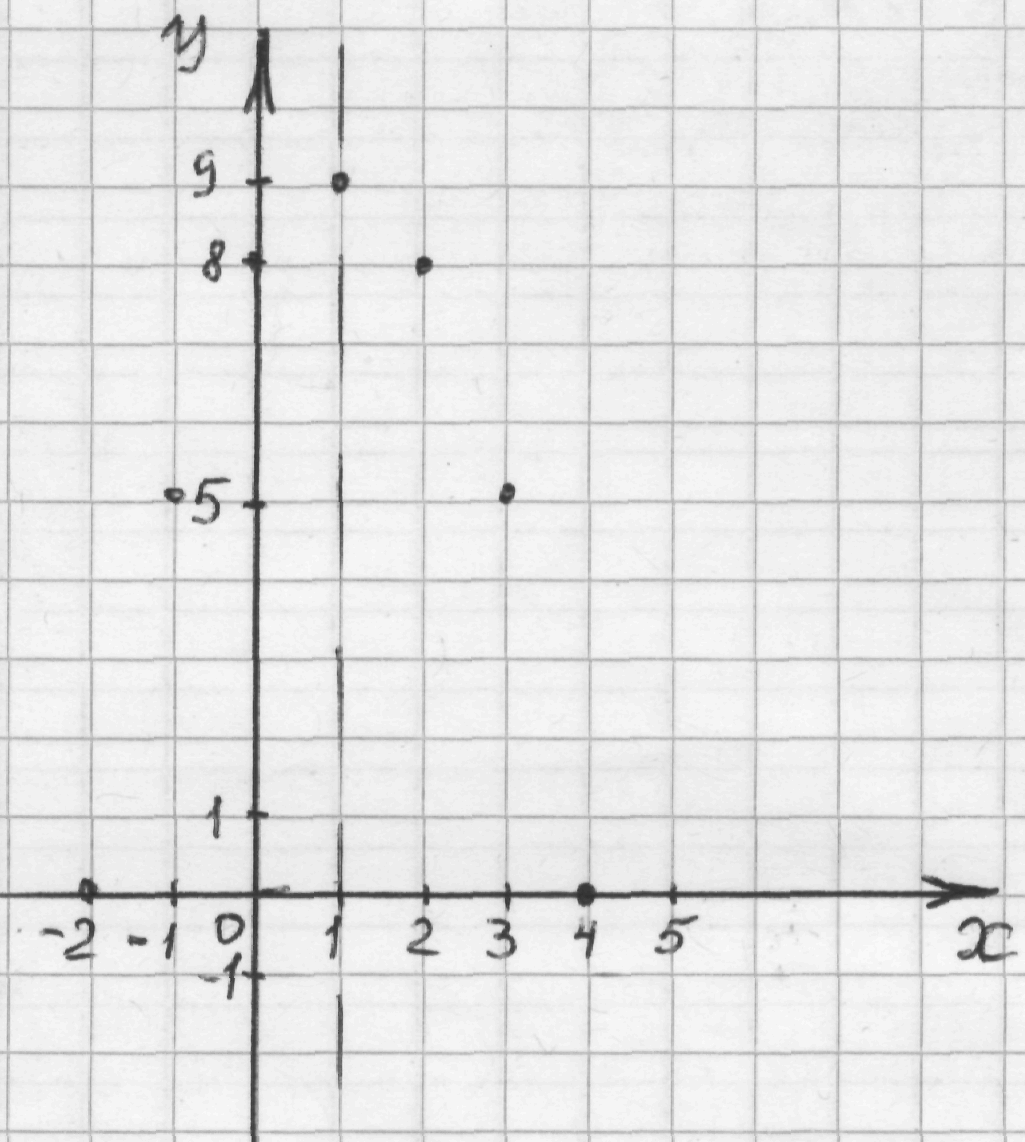
4. Составим таблицу значений:

х

— 2	— 1		1	2	3	4
у		5	8	9	8	5

IV. Тема «НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ»

1. Неравенства второй степени с одной переменной — это неравенства вида ах² + bх + с  0 и ах² + bх + с < 0, где х — переменная, а, b, с — некоторые числа, причем а ≠ 0.

2. Решить неравенство, содержащее переменную, — значит найти множество значений переменной, при которых это неравенство является верным. Элементы этого множества называются решениями неравенства.

Алгоритм 6

Чтобы решить неравенство второй степени с одной переменной, надо:

1. записать функцию у = ах² + bх + с, определить направление ветвей параболы;

2. решить уравнение ах² + bх + с = 0, найти корни уравнения или убедиться, что их нет;

3. если уравнение не имеет корней, т.е. D < 0, то возможны случаи:

1) а  0 и ах² + bх + с  0, решением неравенства является промежуток (−∞; + ∞), т.к. график параболы находится выше оси х;

2) а  0 и ах² + bх + с < 0, неравенство не имеет решения;

3) а < 0 и ах² + bх + с < 0, решением неравенства является промежуток (−∞; + ∞), т.к. график параболы находится ниже оси х;

4) а < 0 и ах² + bх + с  0, неравенство не имеет решения;

4. если уравнение имеет два корня, надо их отметить на оси х и через отмеченные точки провести параболу схематически, учтя направление ветвей;

5. найти на оси промежутки, для которых точки параболы расположены выше оси х (если решают неравенство ах² + bх + с  0) или ниже оси х (если решают неравенство ах² + bх + с < 0).

Пример 1. Решить неравенство 2х² + 13х – 7  0. б) –2х² – 5х + 18 ≤ 0.

Решение:

1) у = 2х² + 13х – 7, ветви вверх;

2) 2х² + 13х – 7 = 0, D = 225  0, два корня, х₁ = – 7, х₂ = 0,5;

3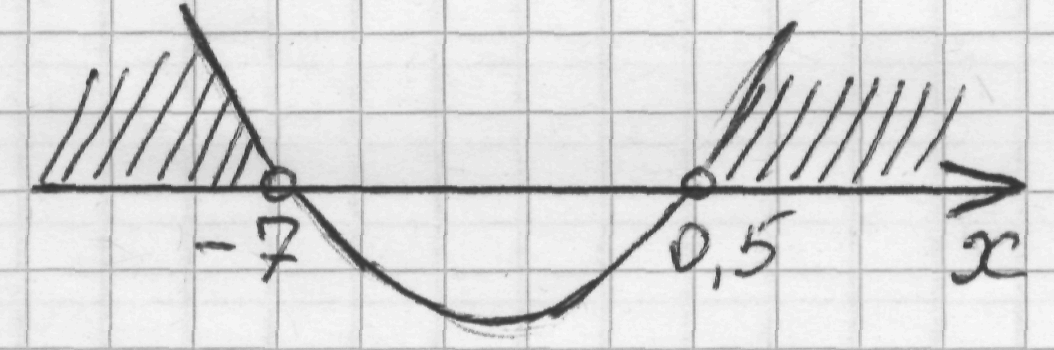) рисунок

4) Ответ: х  (−∞; — 7)  (0,5; + ∞).

Пример 2. Решить неравенство –2х² – 5х + 18 ≤ 0.

Решение:

1) у = –2х² – 5х + 18, ветви вниз;

2) –2х² – 5х + 18 = 0, D = 169  0, два корня, х₁ = – 4,5, х₂ = 2;

3)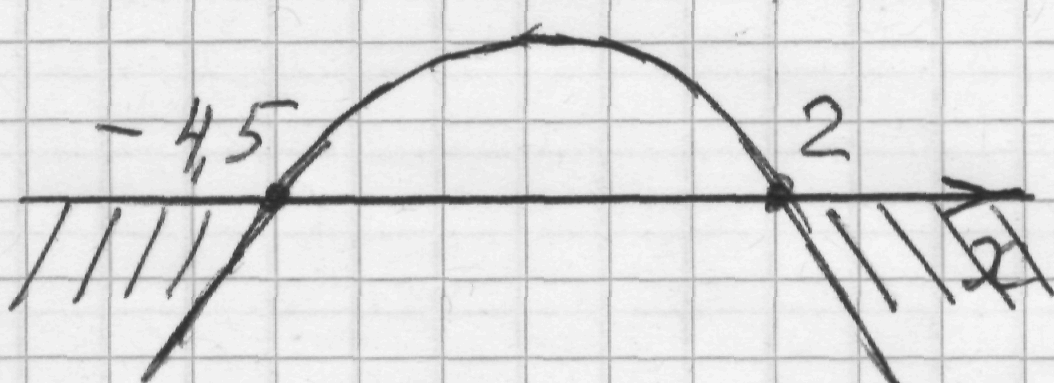

4) Ответ: х  (−∞; — 4,5]  [2; + ∞).

Пример 3. Решить неравенство –2х² – 5х + 18 ≥ 0.

Решение: смотри пример 2.

Ответ: х  [- 4,5; 2].

Если неравенство записано в виде (х – х₁)(х – х₂)…(х – х_п)  0 или (х – х₁)(х – х₂)…(х – х_п) < 0, то его рациональнее решить методом интервалов.

Алгоритм 6

Чтобы решить неравенство с одной переменной (х – х₁)(х – х₂) …(х – х_п)  0 или (х – х₁)(х – х₂) …(х – х_п) < 0 методом интервалов, надо:

1. записать функцию f(x) = (х – х₁)(х – х₂) …(х – х_п);

2. найти нули функции, т.е. решить уравнение (х – х₁)(х – х₂) …(х – х_п) = 0;

3. отметить на координатной прямой найденные значения х;

4. указать знаки функции в образовавшихся промежутках (интервалах);

5. записать ответ, учитывая знак неравенства.

Пример. Решить неравенство методом интервалов: .

Решение:

Запишем неравенство, учтя значения подкоренного выражения: х (х + 9)(2х – 8)  0;

1. f(x) = х (х + 9)(2х – 8);

2. х (х + 9)(2х – 8) = 0, х₁ = 0 или х + 9 = 0 или 2х – 8 = 0,

х₂ = – 9, х₃ = 4;

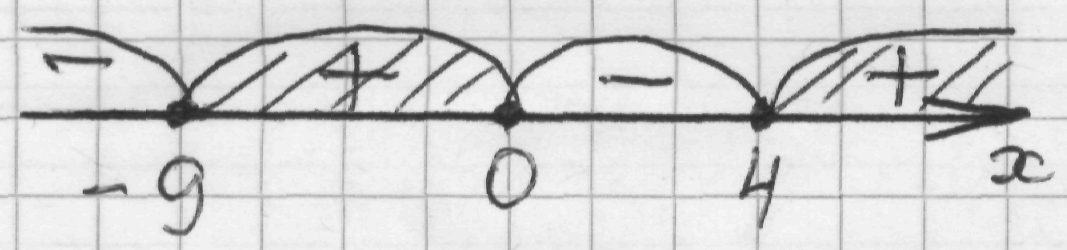
4. Ответ: х  [ – 9; 0]  [4; + ∞).

V. Тема «УРАВНЕНИЯ. СИСТЕМЫ УРАВНЕНИЙ»

Алгоритм 7

Чтобы решить уравнение с одной переменной графическим способом, надо:

1. записать его в виде f(x) = g(x);

2. построить в одной системе координат графики обеих функций;

3. найти абсциссы(у) точек(ки) пересечения функций.

Существует два способа решения системы уравнений с двумя переменными: способ подстановки и способ сложения.

Алгоритм 8

Чтобы решить способом подстановки систему уравнений, в которой одно из уравнений второй степени, надо:

1. выразить из уравнения первой степени одну переменную через другую;

2. подставить полученное выражение в уравнение второй степени;

3. решить полученное квадратное уравнение;

4. подставить найденные значения переменной в уравнение первой степени и вычислить значения второй переменной;

5. записать ответ.

Пример. Решить систему уравнений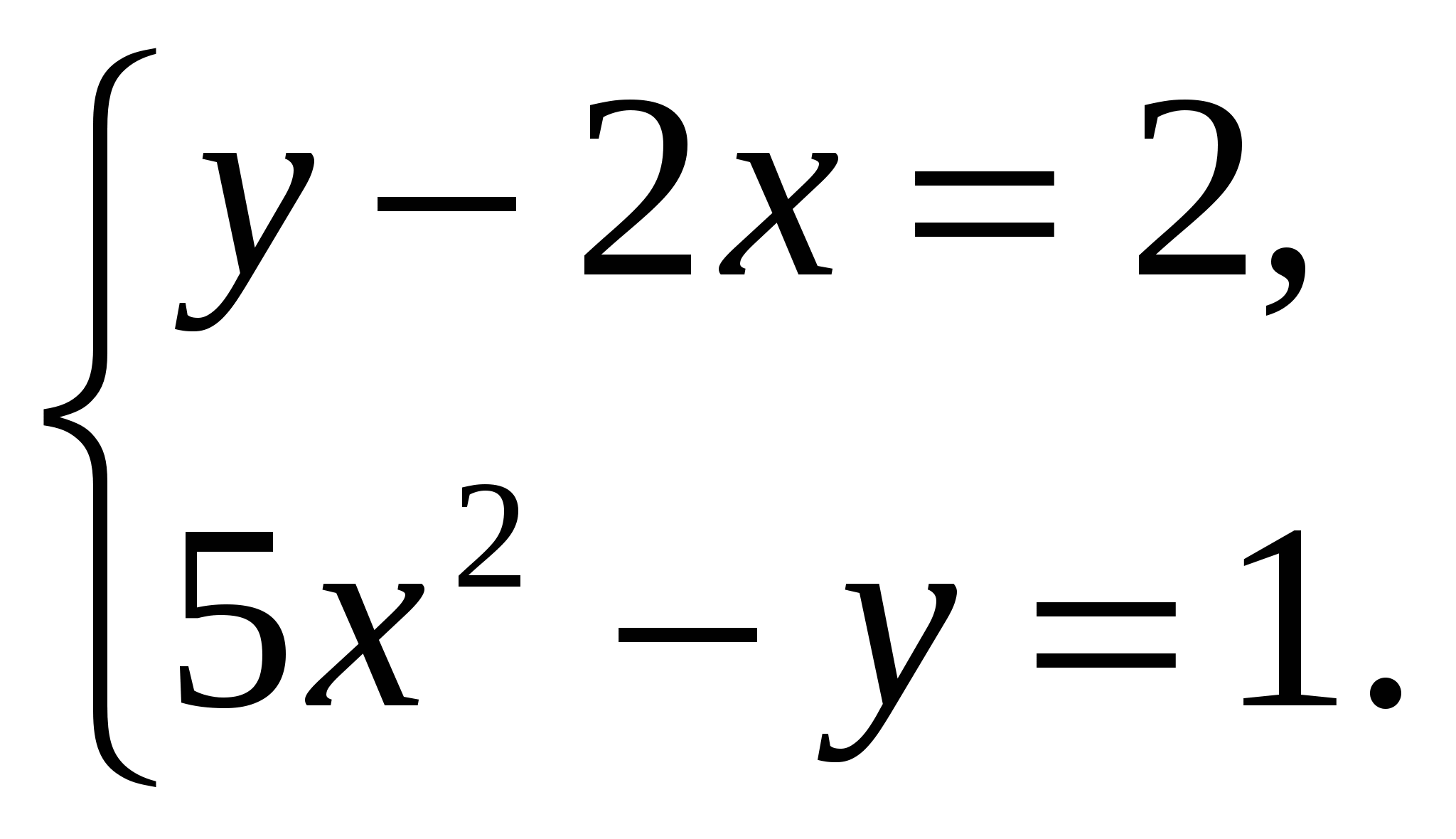

Решение.

1. Выразим переменную у из первого уравнения: у = 2 + 2х.

2. Подставим во второе уравнение вместо у выражение 2 + 2х.

3. 5х² – (2 + 2х) = 1, 5х² – 2х – 3 = 0, D = 64, х₁ = 1, х₂ = – 0,6.

4. у₁ = 2 + 2 · 1 = 4, у₂ = 2 + 2 · (– 0,6) = 0,8.

5. Ответ: (1; 4), (– 0,6; 0,8).

Алгоритм 9

Чтобы решить способом сложения систему уравнений, надо:

1. добиться того, чтобы при одной из неизвестных (при х или у) коэффициенты были противоположными числами;

2. сложить левые и правые части уравнений;

3. решить полученное уравнение с одним неизвестным;

4. подставить найденное(ые) значение(я) переменной в любое уравнение заданной системы и вычислить значение(я) второй переменной;

5. записать ответ.

Пример. Решить систему уравнений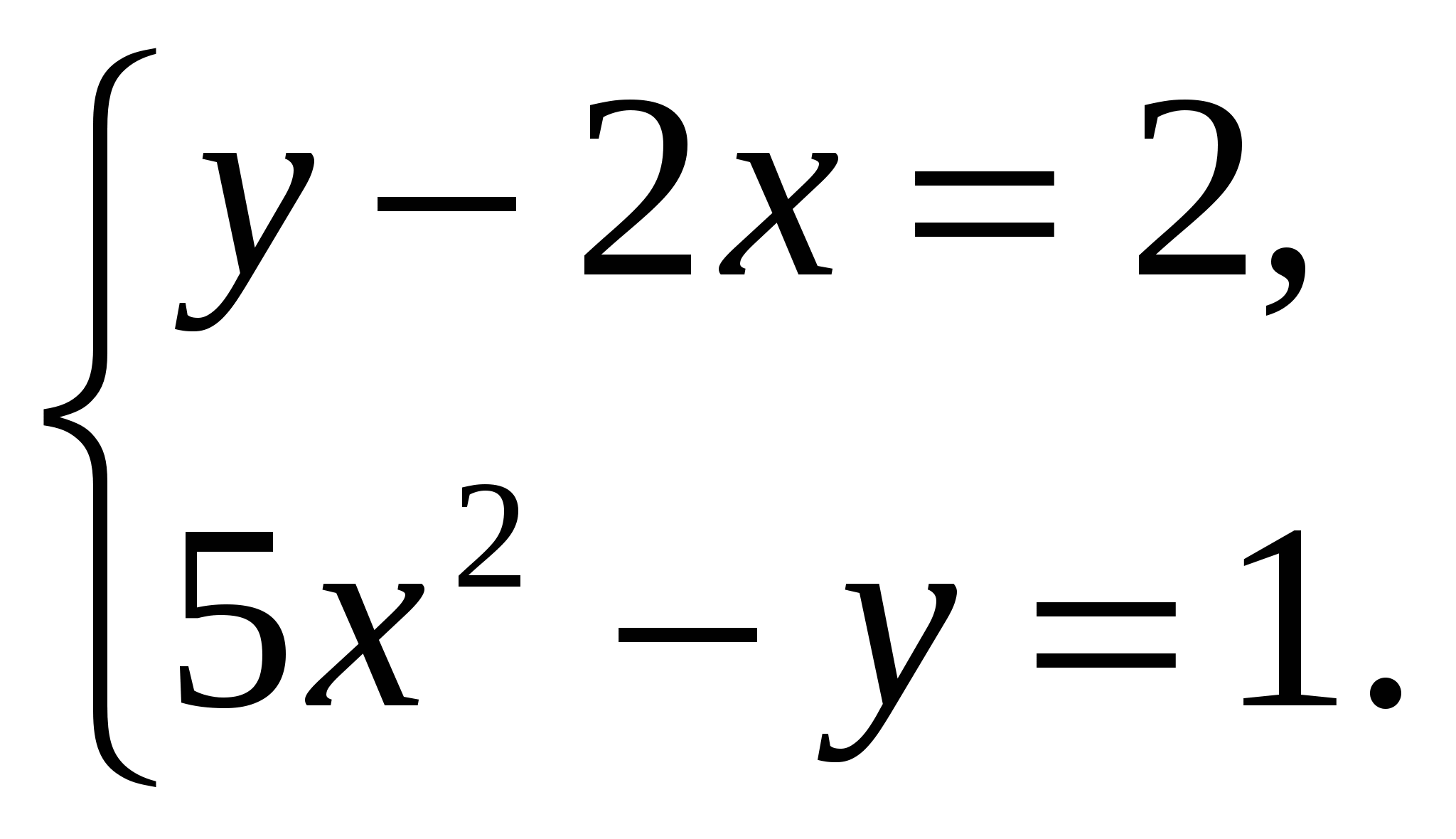

Решение.

1. При неизвестной переменной у коэффициенты являются противоположными числами.

2. Сложим почленно левые и правые части уравнений:

3. +

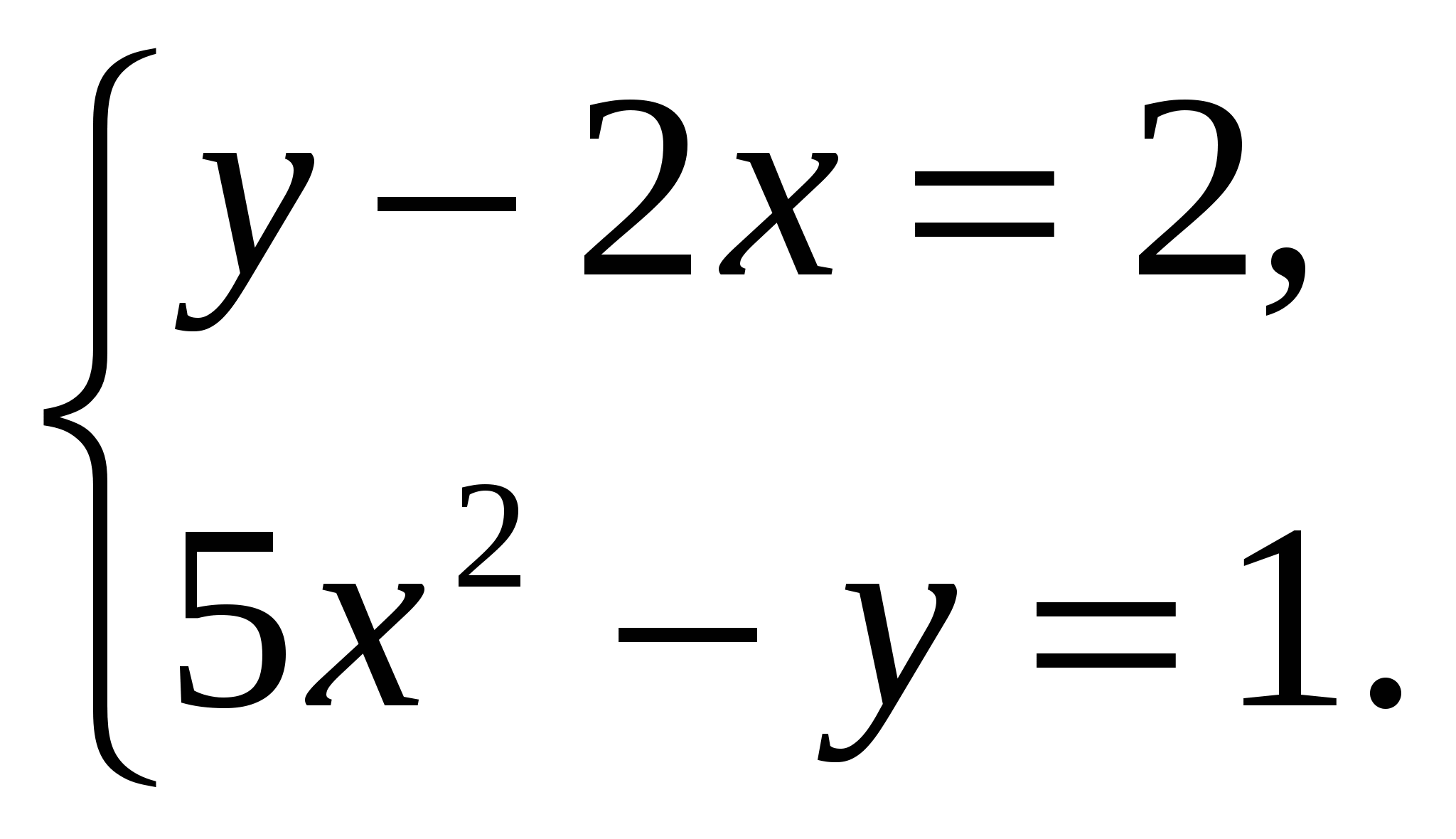
5х² – 2х = 3

4. Решим полученное уравнение с одним неизвестным: 5х² – 2х – 3 = 0, D = 64, х₁ = 1, х₂ = – 0,6.

5. Подставим найденные значения х в первое (можно во второе) уравнение: у₁ – 2 · 1 = 2, у₁ = 4; у₂ – 2 · (– 0,6) = 2, у₂ = 0,8.

6. Ответ: (1; 4), (– 0,6; 0,8).

VI. Тема «АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ»

Основные понятия и формулы.

1. Арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом.

2. Разностью арифметической прогрессии называется разность между любым членом арифметической прогрессии и ему предшествующим, т.е. d = а_п+1 – а_п.

3. Формула п-го члена арифметической прогрессии а_п = а₁ + d (п – 1);

4. Формулы суммы п первых членов арифметической прогрессии

(I) и (II).

Алгоритм 10

Чтобы найти сумму п первых членов арифметической прогрессии, надо:

1. записать значения п и а₁;

2. найти по условию d или а_п;

3. подставить найденные значения в формулу и вычислить.

Пример.

Найти сумму первых тридцати членов арифметической прогрессии (а_п): 20; 18,5;…

Решение.

1. Запишем п = 30, а₁ = 20;

2. Найдем по условию d = а_п+1 – а_п = 18,5 – 20 = – 1,5;

3. Воспользуемся формулой (II)

.

Если решили воспользоваться формулой (I), то:

1. запишем п = 30, а₁ = 20;

2. найдем по формуле а_п = а₁ + d (п – 1) а₃₀ = 20 + (– 1,5) · (30 –1) = – 23,5;

3. по формуле (I) .

VII. Тема «ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ»

Основные понятия и формулы.

1. Геометрической прогрессией называется числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему члену, умноженному на одно и то же число, не равное нулю.

2. Отношение любого члена геометрической прогрессии к предшествующему называется знаменателем прогрессии .

3. Формула п-го члена геометрической прогрессии ;

4. Формулы суммы п первых членов геометрической прогрессии при q ≠ 1

(I) и (II).

Алгоритм 11

Чтобы найти сумму п первых членов геометрической прогрессии, надо:

1. записать значения п и b₁;

2. найти по условию q или b_п;

3. подставить найденные значения в формулу и вычислить.

Пример. Найти сумму первых восьми членов геометрической прогрессии (b_п): ; 1; …

Решение.

1. Запишем значения п = 8 и b₁ = .

2. Найдем по условию q = 1 : (1/2) = 2.

3. По формуле (II): .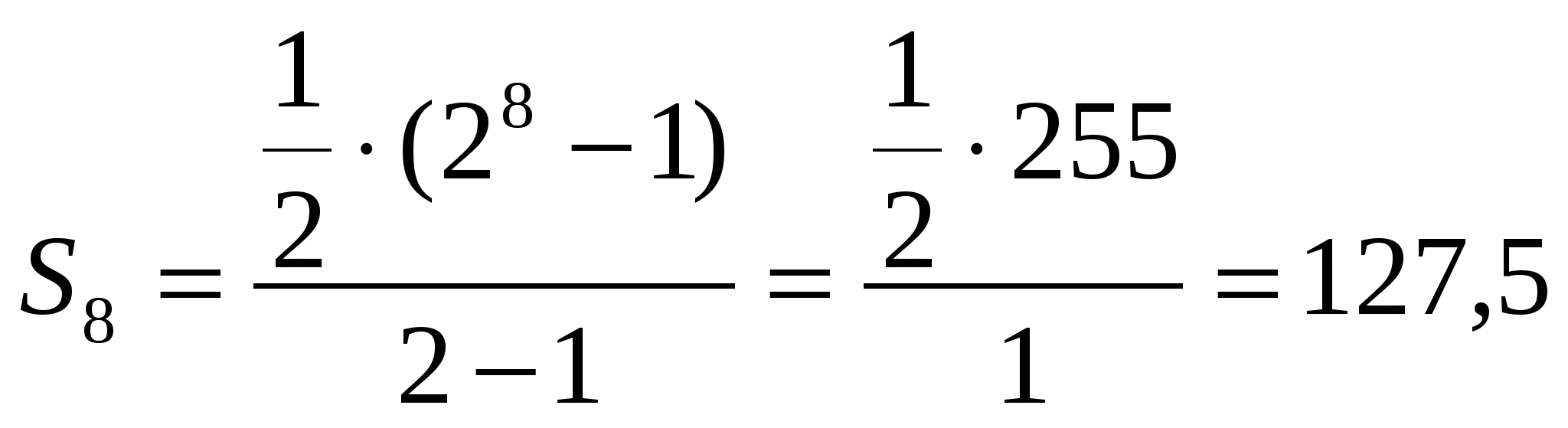

Если решили воспользоваться формулой (I), то:

1. запишем значения п = 8 и b₁ = ;

2. найдем по условию q = 1 : (1/2) = 2 и ;

3. по формуле (I): .

Тема «Тригонометрические выражения и их преобразования» не является обязательной в курсе алгебры 9 класса, задания этого раздела не выносятся на экзамен. Однако учащимся, которые планируют получить среднее образование, основные понятия и тригонометрические формулы знать необходимо, т.к. курс «Алгебра и начала анализа 10-11» предполагает изучение данной темы в 9 классе.

VIII. Тема «ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЛЮБОГО

УГЛА»

Для измерения углов используется две единицы измерения — градус и радиан.

Напомним, что угол в 1 радиан есть центральный угол, опирающийся на такую дугу окружности, длина которой равна радиусу этой окружности.

Алгоритм 12

Чтобы перевести градусную меру в радианную, надо:

1. величину угла умножить на ;

2. сократить полученное выражение.

Пример.

Выразить в радианной мере углы а) 60º, б) 135º, в) 250º.

Решение. а) 60º = ; б) 135º = ;

в) 250º = .

Алгоритм 13

Чтобы перевести радианную меру в градусную, надо:

1. величину угла умножить на ;

2. сократить полученное выражение.

Пример.

Найти градусную меру угла а) 10; б) ; в) 12π.

Решение: а) 10 рад = 10 · = ; б) ;

в) 12π = 12π · = 2160º.

Справочный материал

1. Синус угла α — это отношение ординаты точки Р_α к радиусу.

2. Косинус угла α — это отношение абсциссы точки Р_α к радиусу.

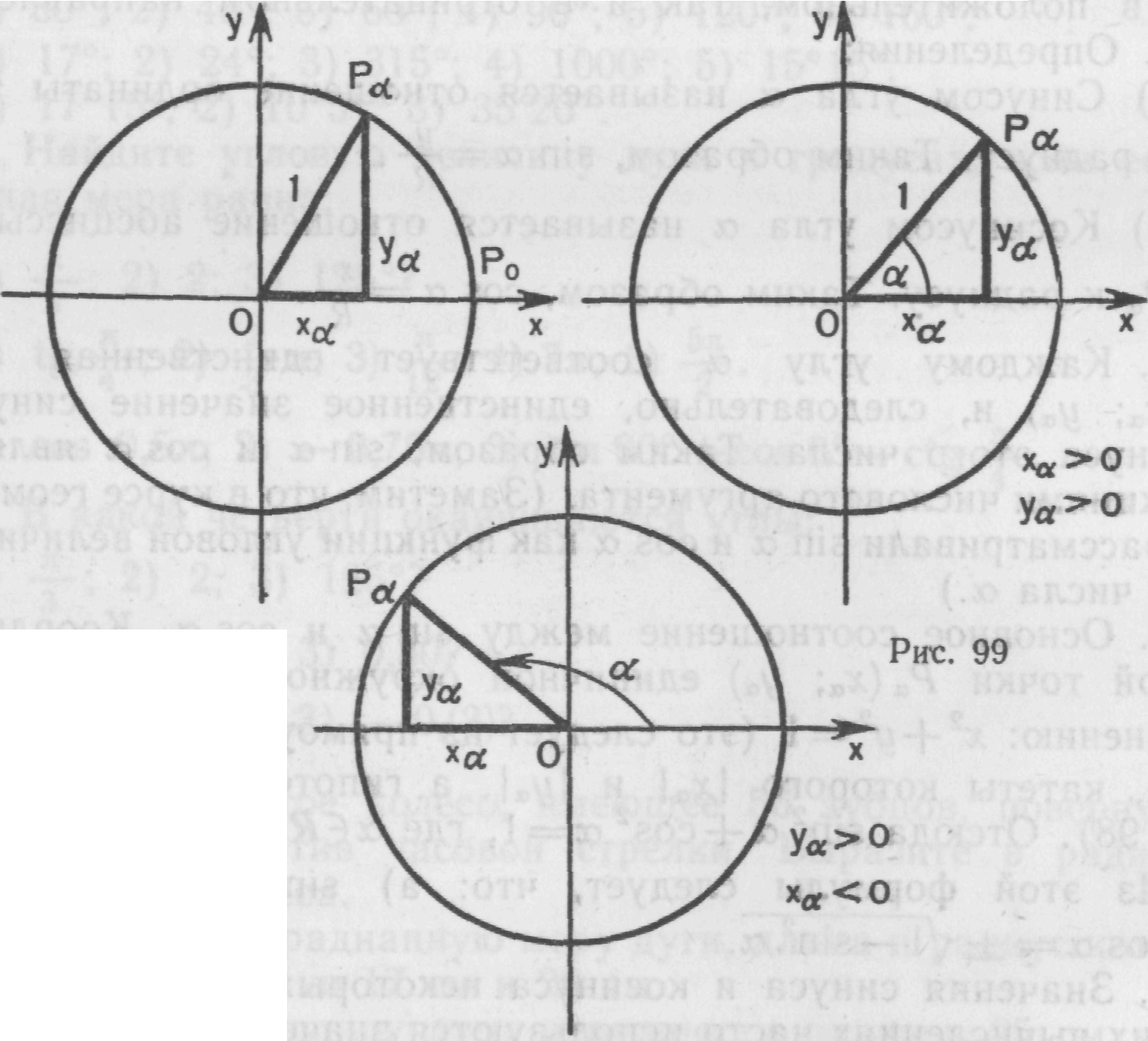
3. Тангенс угла α — это отношение ординаты точки Р_α к абсциссе.

4. Котангенс угла α — это отношение абсциссы точки Р_α к ординате.

α

	30º	45º	60º	90º	180º	270º	360º
					π
sin α					1		— 1
cos α	1					— 1		1
tg α			1		—		—
ctg α	—		1			—		—

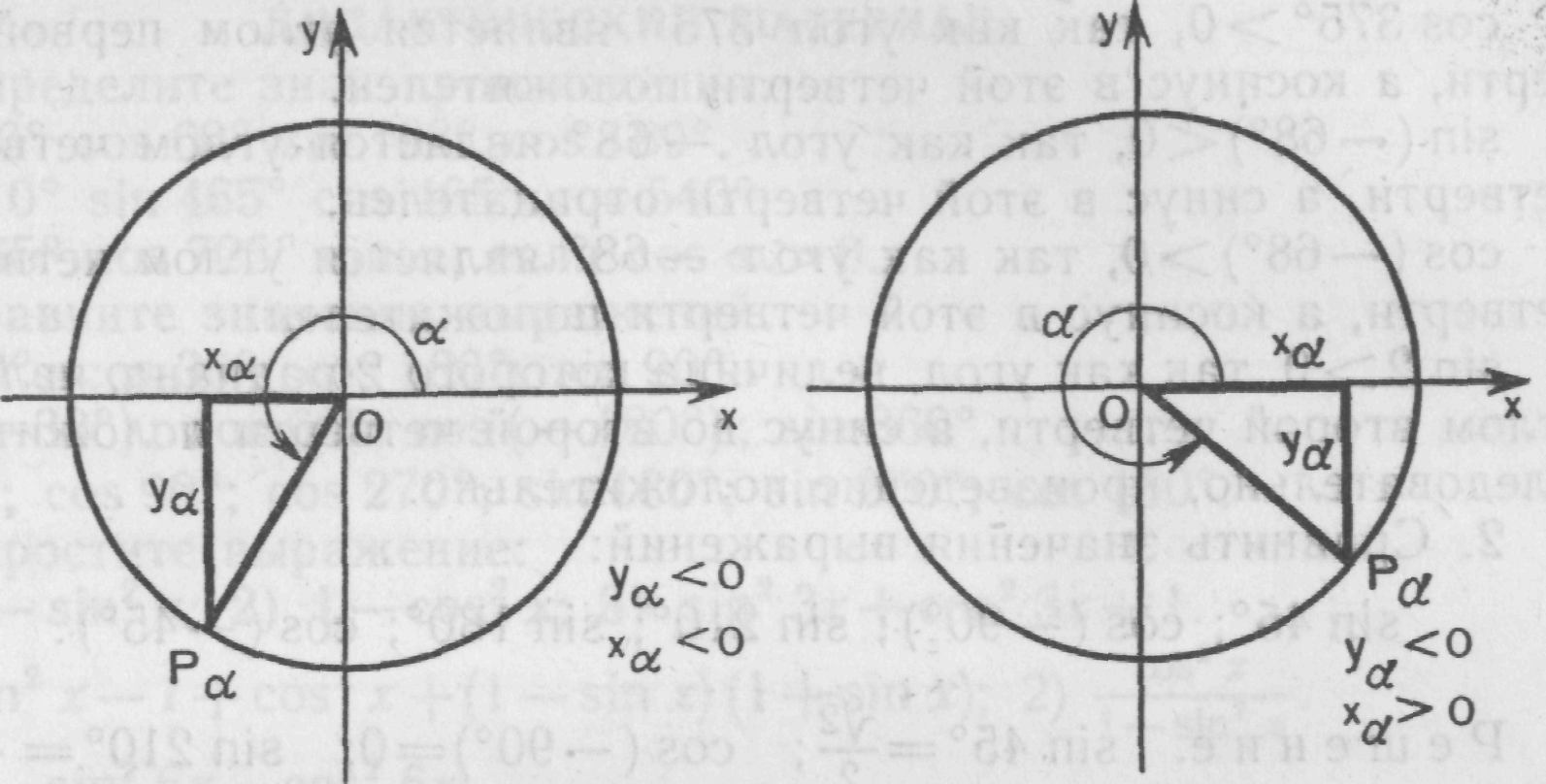
Координатная плоскость

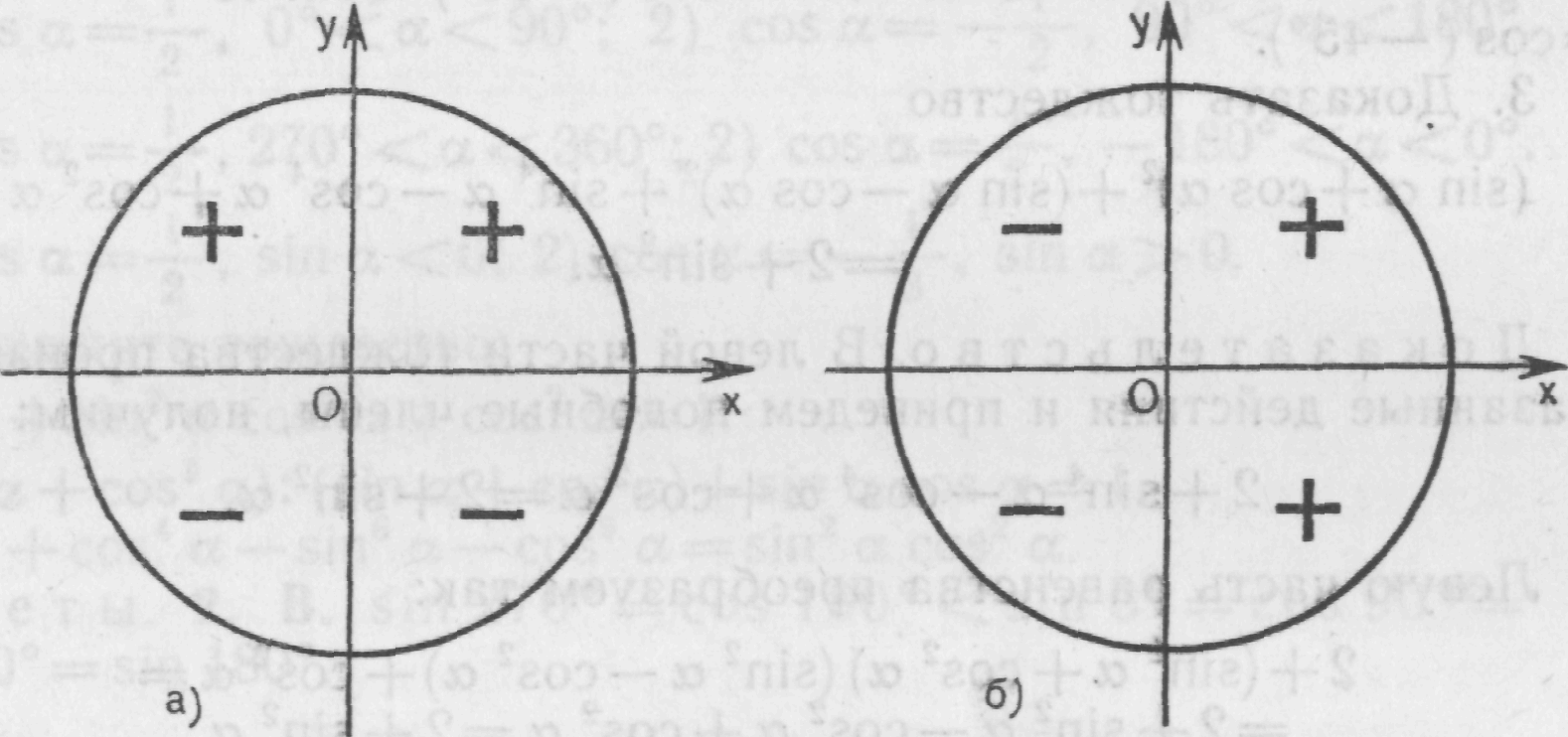
Ι четверть: 0º < α < 90º или 0 < α < .

Значения вс