Назарбаев Интеллектуальная школа физико- математического направления
г. Кокшетау Акмолинская область
Конспект урока по информатике
в 6 классе
«Граф.
Решение задач с помощью графа».
Подготовила учитель информатики
Нурмуханова Асель Сериковна
Кокшетау
2011
Тема урока: Граф. Решение задач с помощью графа.
Цель урока: Составить представление об организации информации в виде дерева (графа). Освоить понятие граф. Научиться решать задачи с помощью графов.
| Ученик знает назначение графов | |
| Понимание | Умеет приводить примеры использования графов в различных учебных предметах (химия, информатика, биология, геометрия и др.) и повседневной жизни. |
| Применение | Умеет записывать арифметические выражения в виде графов, отражать информацию в виде семантической сети, изображать классификации различных объектов в виде дерева |
| Анализ | Умеет из множества предметов вычленить объекты, обозначить связи между ними. |
Оборудование: компьютер, таблицы, карточки. Длительность урока:40 мин
План урока
I этап – Орг.момент (3 мин)
II этап – Новая тема. Понятие графа.(8 мин)
Графы являются существенным элементом математических моделей в самых разнообразных областях науки и практики. Они помогают наглядно представить взаимоотношения между объектами или событиями в сложных системах. Многие алгоритмические задачи дискретной математики могут быть сформулированы как задачи, так или иначе связанные с графами, например задачи, в которых требуется выяснить какие-либо особенности устройства графа, или найти в графе часть, удовлетворяющую некоторым требованиям, или построить граф с заданными свойствами.
Легко найти примеры графов в самых разных областях науки и практики. Сеть дорог, трубопроводов, электрическая цепь, структурная формула химического соединения, блок-схема программы
Решение многих математических задач упрощается, если удается использовать графы. Представление данных в виде графа придает им наглядность и простоту. Многие математические доказательства также упрощаются, приобретают убедительность, если пользоваться графами. Для решения логических задач удобно использовать графы.
Графы – это рисунки, которые состоят из точек и линий, соединяющих эти точки.
Каждая пара точек в графе может быть соединена линиями. Линия указывает на связь между двумя точками.
Точки называются вершинами графа, а линиями рёбрами.
Ребро может иметь направление, которое указывается стрелочкой.
У графа обязательно есть вершины.
Граф без рёбер называется пустым.
Примеры различных графов приведены на рисунке.
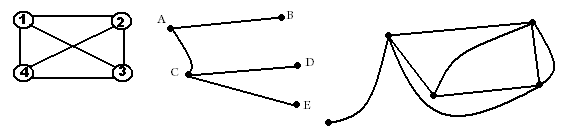
Дерево (граф) – это способ организации информации об отношениях между объектами.
Слово «дерево» в теории графов означает граф, в котором нет циклов, то есть в котором нельзя из некоторой вершины пройти по нескольким различным ребрам и вернуться в ту же вершину.
Первая работа по теории графов принадлежит Леонардо Эйлеру (1736г).
Термин граф впервые ввёл 1936г Венгерский математик Денеш Кениг. Графами были названы схемы состоящие из точек и соединяющие эти точки отрезков прямых или кривых.
С помощью графов часто упрощалось решение задач, сформулированных в разных областях знаний: в автоматике , электронике, физике, химии.
С помощью графов изображаются схемы дорог, газопроводов, тепло и электро сетей.
Графы в которых не построены все возможные рёбра называется не полными графами.
III этап. Представление информации в виде дерева. (2 мин)
Особым видом графа является дерево. Данная форма модели применяется тогда, когда элементы моделируемого объекта находятся в состоянии какого-либо подчинения и соподчинения, когда есть отношение иерархичности. Модель управления предприятием (школой, театральным коллективом и т. д.) очень удобно представлять в виде дерева.
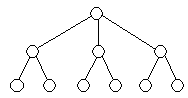
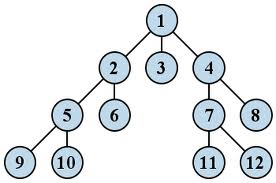
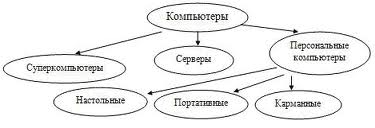
Описать граф- это значит, ответить на вопросы:
Сколько вершин?
Есть рёбра?
Есть направление?
Все ли вершины соединены рёбрами?
На каких школьных предметах вы встречались с графами, приведите примеры?
Учитель приводит несколько примеров. Вам хорошо известно понятие «родословное дерево» и вы можете изобразить в такой форме ваши родственные отношения. Каталог файлов на диске, также как и библиотечный каталог — примеры информационных моделей в форме дерева.
I V этап.Заполнение схемы. Применение графа. (3мин)
V этап.Заполнение схемы. Применение графа. (3мин)
V этап. Применение знаний и закрепление изученного. (15 мин)
Рассмотрим одну из простейших задач: «Красный, синий, желтый и зеленый карандаши лежат в четырех коробках по одному. Цвет карандаша отличается от цвета коробки. Известно, что зеленый карандаш лежит в синей коробке, а красный не лежит в желтой. В какой коробке лежит каждый карандаш?»
О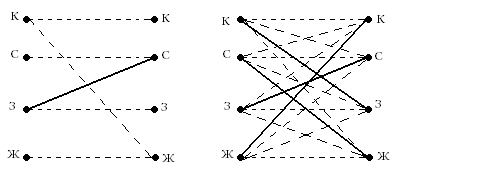 бозначим точками карандаши и коробки. Сплошная линия будет обозначать, что карандаш лежит в соответствующей коробке, а пунктирная, что не лежит. Тогда с учетом задачи имеем граф (1).
бозначим точками карандаши и коробки. Сплошная линия будет обозначать, что карандаш лежит в соответствующей коробке, а пунктирная, что не лежит. Тогда с учетом задачи имеем граф (1).
Далее достраиваем граф по следующему правилу: поскольку в каждой коробке может лежать ровно один карандаш, то из каждой точки должны выходить одна сплошная линия и три пунктирные. Получается граф (2) дающий решение задачи.
Задача1: Алия решила маме на день рождения подарить букет цветов (розы, тюльпаны или гвоздики) и поставить из или в вазу или в кувшин.
Сколькими способами это можно сделать.
Решение. Отметим точками цветы (РТГВК) (вершины графа)
А связи между ними -линиями между точками (рёбра графа)
По рисунку видно, что таких сопопбов — 6
*
 розы * тюльпан *гвоздики
розы * тюльпан *гвоздики
* ваза *кувшин
Задача2. Ранним утром Миша Маша, Асем обменялись приветствиями каждый с каждым. Сколько всего было приветствий. Решите задачу с помощью графа. Нарисуй граф в рабочей тетради.
Задача3. Шесть футбольных команд должны сыграть матчи, каждая с каждой. Уже сыграли матчи.
А с В, Г,Е Г с А,Д,Е
Б с В,Д,Е Д с Б,Г,Е
В с А,Б Е с А,Б,Г,Д
Сколько матчей сыграно и сколько осталось сыграть.
Задача4. Мадии утром собрался в школу, но по пути он должен зайти в аптеку за лекарствами. Сколькими способами он может это сделать.
Задача5. В квартирах №1,2,3 жили три друга: Айдар, Тима и Саша. Известно, что в квартирах №1 и 2 жил не Айдар. Тима жил не в квартире №1. В какой квартире жил каждый из друзей.
Ответ:
| Айдар | Тима | Саша | |
| №1 | — | — | + |
| №2 | — | + | — |
| №3 | + | — | — |
Задача6. Арман, Мадии, Тимур, Сергей заняли на математической олимпиаде четыре первых места. Когда их спросили о распределений мест, они дали три ответа: Сергей – первый, Мади– второй, Сергей -второй, Арман – третий, Тимур – второй, Арман – четвертый. Известно, что в каждом ответе только одно утверждение верно. Как распределились места?
Ответ: С-1 Т-2 А -3 М-4.
Задача7. Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было сыграно?
Решение: Решим задачу с помощью полного графа с четырьмя вершинами А, Б, В, Г, обозначенными по первым буквам имен каждого из мальчиков. В полном графе проводятся всевозможные ребра.
В данном случае отрезки-ребра обозначают сыгранные шахматные партии. Из рисунка видно, что граф имеет 6 ребер, значит, и партий было сыграно 6.
Задача8.Из города А в город Б ведут две дороги, из города Б в городок В -тоже две дороги и из города А в город В – тоже две дороги. Нарисуй схему и сосчитай все возможные пути из города А в город В. Ответ: 6 партий .
Задача9. Андрей, Борис, Виктор и Григорий после возвращения из спортивного лагеря подарили на память друг другу свои фотографии. Причем каждый мальчик подарил каждому из своих друзей
по одной фотографии. Сколько всего фотографий было подарено?
Р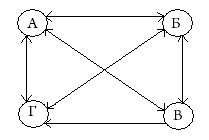 ешение. I способ. С помощью стрелок на ребрах полного графа с вершинами А, Б, В и Г показан процесс обмена фотографиями. Очевидно, стрелок в 2 раза больше, чем ребер, т.е. 6*2 = 12. Столько же было подарено и фотографий.
ешение. I способ. С помощью стрелок на ребрах полного графа с вершинами А, Б, В и Г показан процесс обмена фотографиями. Очевидно, стрелок в 2 раза больше, чем ребер, т.е. 6*2 = 12. Столько же было подарено и фотографий.
II способ. Каждый из четверых мальчиков подарил друзьям 3 фотографии, следовательно, всего было роздано 3 • 4 = 12 фотографий.
О т в е т: 12 фотографий.
VI этап. Рефлексия. (5 мин)
«Почему понятие графа изучается в школьном курсе информатики?»
Дополнительные вопросы:
Нужно ли на уроках информатики знакомиться с понятием графа и учиться строить их?
Как вы считаете, с какой целью было введено понятие графа в школьный курс информатики?
Какие качества личности позволяет развить умение строить графы?
Попробуйте сделать вывод о значении информатики и графов в частности для остальных учебных предметов. Информатика дает инструмент для познания любой научной дисциплины.
VII этап. Домашнее задание: Дополнить схему примерами применения графов. (1 мин)
VIII этап. Итог урока. Выставление оценок. (1 мин)
Список литературы:
1. Нагибин Ф.Ф. Применение графов для решения логических задач.
// Математика в школе. — 1964. — № 3.
2. Шедивы Я. Решение логических задач при помощи графов.
// Математика в школе. — 1967. — № 6.
3. Березина Л.Ю. Графы помогают решать логические задачи.
// Математика в школе. — 1972. — № 2.
4. Федосеев В.Н. Элементы теории вероятностей для VII—VIII классов средней школы.
// Математика в школе. — 2002. — № 4.
