План-конспект урока по математике «Теорема Пифагора»

План-конспект урока по теме «Теорема Пифагора» 

Цели урока:

1. Изучить некоторые исторические сведения о Пифагоре и его теореме, доказательство теоремы Пифагора, следствия, значение теоремы; усвоить и отработать алгоритм решения задач по данной теме

2. Способствовать развитию математического и общего кругозора, мышления и речи, ясности и точности мысли, внимания и памяти, формированию элементов алгоритмической культуры

3. Содействовать воспитанию интереса к математике, культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии; формировать умения работать с информацией, развивать коммуникативные способности учащихся.

Ход урока

I. Подготовка к уроку

II. Проверка домашнего задания

Дано:
∆ АВС, ∆ А₁B₁С₁, ∠ С = ∠ С₁ = 90°
А₁B₁ = 7 см, А₁С₁= 4 см
АB = 21 см, ∠ А = ∠ А1

Найти: АС

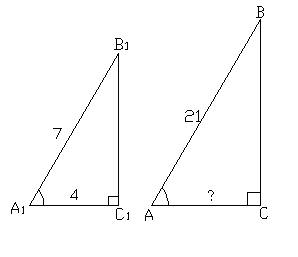
Решение:

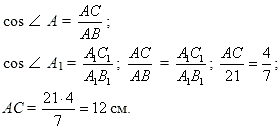
Ответ: 12 см

III. Подготовка к изучению нового материала

Сегодня мы познакомимся с одной из немногих теорем геометрии, которую помнят все учащиеся.

Проверим готовность к восприятию нового материала.

1. Какой треугольник изображен на рисунке 1? Назовите катеты и гипотенузу. Выразите cos ∠ M, cos ∠ P.

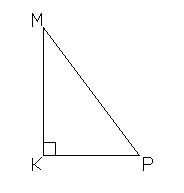
Рисунок 1

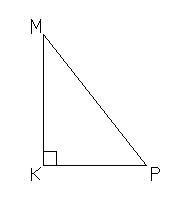
2. Какой треугольник изображен на рисунке 2? Чем он интересен?

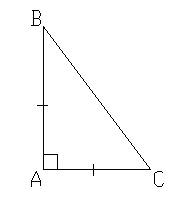
Рисунок 2

3. Какой треугольник изображен на рисунке 3?

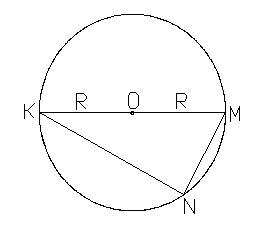
Рисунок 3

Прежде чем мы совершим путешествие по страницам науки геометрии, решим кроссворд.

1. Сторона прямоугольного треугольника.

2. Отношение прилежащего катета к гипотенузе.

3. Имя ученого, доказавшего теорему о параллельных прямых, пересекающих стороны угла.

4. Утверждение о свойстве той или иной геометрической фигуры, не требующее доказательства.

5. Параллелограмм с прямым углом.

6. Фигура, состоящая из трех точек, не лежащих на одной прямой и…

7. Четырехугольник, у которого противолежащие стороны параллельны.

Расскажем о Пифагоре, именем которого названа теорема, которую знают все.

Сообщение ученика.

В Древней Греции жил ученый Пифагор (родился он около 580 г. до н. э., а умер в 500 г. до н. э.). О жизни этого ученого известно немного, зато с его именем связано ряд легенд. Рассказывают, что он много путешествовал, был в Индии, Египте, Вавилоне, изучал древнюю культуру и достижения науки разных стран. Вернувшись на родину, Пифагор организовал кружок молодежи из представителей аристократии. В кружок принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Так на юге Италии, которая была тогда греческой колонией, возникла так называемая пифагорейская школа. Пифагорейцы занимались математикой, философией, естественными науками. Ими было сделано много важных открытий в арифметике и геометрии. В школе существовал декрет, по которому авторство всех математических работ приписывалось Пифагору. Пифагор был убит в уличной схватке во время народного восстания. После его смерти ученики окружили имя своего учителя множеством легенд, так что установить о Пифагоре правду невозможно.

Ребята, знаете ли вы что-нибудь связанное с именем Пифагора?

Запишем тему урока «Теорема Пифагора».

В современных учебниках теорема сформулирована так: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.»

Нарисуем прямоугольный треугольник и запишем эту формулировку в обозначениях:
∆ ABC, ∠ С = 90˚, АВ² = АС² + ВС² или c² = a² +b²

Во времена Пифагора формулировка теоремы звучала так: «Доказать что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах» или «Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах».

Теорема Пифагора имеет богатую историю. Оказывается, она задолго до Пифагора была известна египтянам, вавилонянам, китайцам и индийцам. Доказательство самого Пифагора до нас не дошло. В настоящее время имеется свыше 100 доказательств. Возможно, что одно из них принадлежит Пифагору и его ученикам.

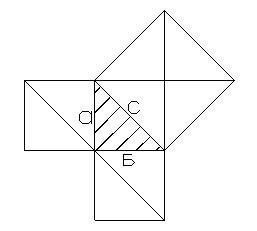
Из рисунка видно, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. Переворачиваем рисунок, а вот и «Пифагоровы штаны на все стороны равны».

IV. Объяснение нового материала

Итак, докажем, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано:
∆ ABC, ∠ С = 90˚

Доказать:
АВ² = АС² + ВС²

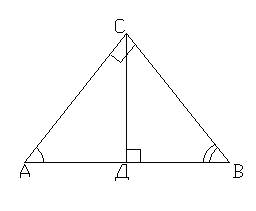
Доказательство:

1. Дополнительное построение: CD – высота ∆ ABC, CD ⊥ AB.

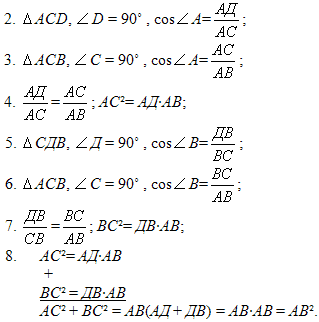
Итак, АВ² = АС² + BС². Ч.т.д.

Из теоремы Пифагора следует, что

Следствие 1: В прямоугольном треугольнике любой из катетов меньше гипотенузы.
Доказательство: По теореме Пифагора АВ² = АС² + BС² так как ВС² > 0, то АВ² > АС², т.е. АС² < АВ², т.е. АС < АВ.

Следствие 2: Для любого острого угла α cos α < 1.
Доказательство: По определению cos α = AC / AB, но по следствию 1: АС > АВ, значит дробь меньше 1.

V. Закрепление. Решение упражнений

№1

Дано:
∆ ABC, ∠ С = 90˚
АС = 6 см, ВС = 8 см

Найти: АВ

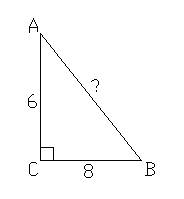
Решение:
По теореме Пифагора:
АВ² = АС² + BС² = 6² + 8² = 36 + 64 = 100
АВ = √100 = 10 см

Ответ: 10 см

№2

Дано:
∆ ABC, ∠ С = 90˚
АС = 3 см, АВ = 5 см

Найти: BC

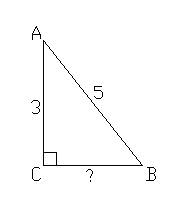
Решение:
По теореме Пифагора:
АВ² = АС² + ВС²
ВС² = АВ² — АС² = 5² — 3² = 25 — 9 = 16,
ВС = √16 = 4 см

Ответ: 4 см

№3

Решим старинную задачу. Она взята из первого учебника математики на Руси. Называется этот учебник «Арифметика». Автор этого учебника Леонтий Филиппович Маницкий. Однако настоящая его фамилия Телятин, а Маницким он стал по приказу Петра I, который был восхищен его занятиями, притягивавшими к себе всех любознательных подобно магниту.

Читаю задачу так, как она была записана в те времена.

«Случился некому человеку к стене лестницу прибрати, стены же тая высота есть 117 стоп. И обреете лестницу долготою 125 стоп. И ведати хощет, колико стоп сея лестницы нижний конец от стены отстояти инать.»

Дано:
∆ ABC, ∠ С = 90˚
АС = 117 стоп, АВ = 125 стоп

Найти: ВС

1 стопа (русск.) = 1 фут (анг.) = 31 см

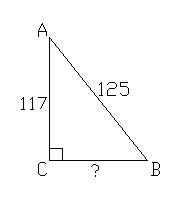
Решение:
По теореме Пифагора
АВ² = АС² + ВС²
ВС² = АВ² — АС² = 125² — 117² = (125 — 117) (125 + 117) = 8 · 242
ВС = √(8 · 242) = √(4 · 2 · 2 · 121) = √4 · √4 · √121 = 2 · 2 · 11 = 44 стопы

Ответ: 44 стопы

VI. Итог урока. Задание на дом

1) Теорема Пифагора – одна из главных и, можно сказать, самая главная терема геометрии. Значение ее состоит в том, что можно вывести большинство теорем геометрии. Теорема Пифагора замечательна и тем, что сама по себе она вовсе не очевидна. Например, свойства равнобедренного треугольника можно непосредственно увидеть на чертеже, но сколько ни смотри на прямоугольный треугольник, никак не увидишь, что между его сторонами есть простое соотношение: с² = а² + в²
2) О чем надо помнить, применяя теорему Пифагора?
3) В чем суть теоремы Пифагора?
4) Комментирование оценок.
5) Вопросы учащихся. Слова признательности ученикам за сотрудничество на уроке.
6) п.63,64. №2(3), №3(2,3), №4, №18.

Дополнительно к уроку

Составьте по рисункам, используя теорему Пифагора, если это возможно, верное равенство.

1) (x² = 3² + 4²)

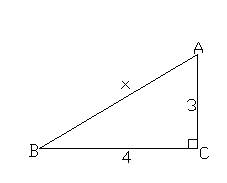
2) (d² = 6² + 8²)

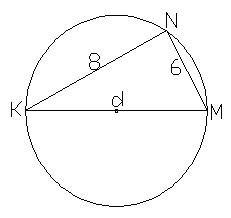
3) (Использовать теорему Пифагора нельзя)

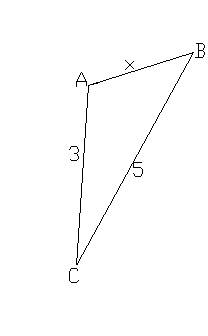
4) а = 1, b = 2, с = 3 (Такого треугольника не существует)

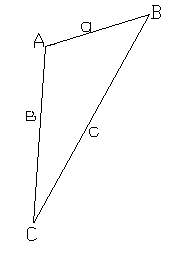
5. Сторона квадрата равна а см. Найти длину диагонали.

5. Диагонали ромба равны 14 см и 48 см. Найдите сторону ромба.

Список используемой литературы

1. Александров А.Д. и др. Геометрия 8/9. М. «Просвещение» 2001.

2. Виленкин Н.Я. и др. За страницами учебника математики. М. «Просвещение» АО «Учебная литература» 1996.

3. Видео. Пифагор.

4. Глейзер Г.И. История математики в школе. М. «Просвещение» 1995.

5. Савин А.П. Энциклопедический словарь юного математика. М. «Просвещение» 1995.

6. Погорелов А.В. Геометрия 7-9. М. «Просвещение» 2010.